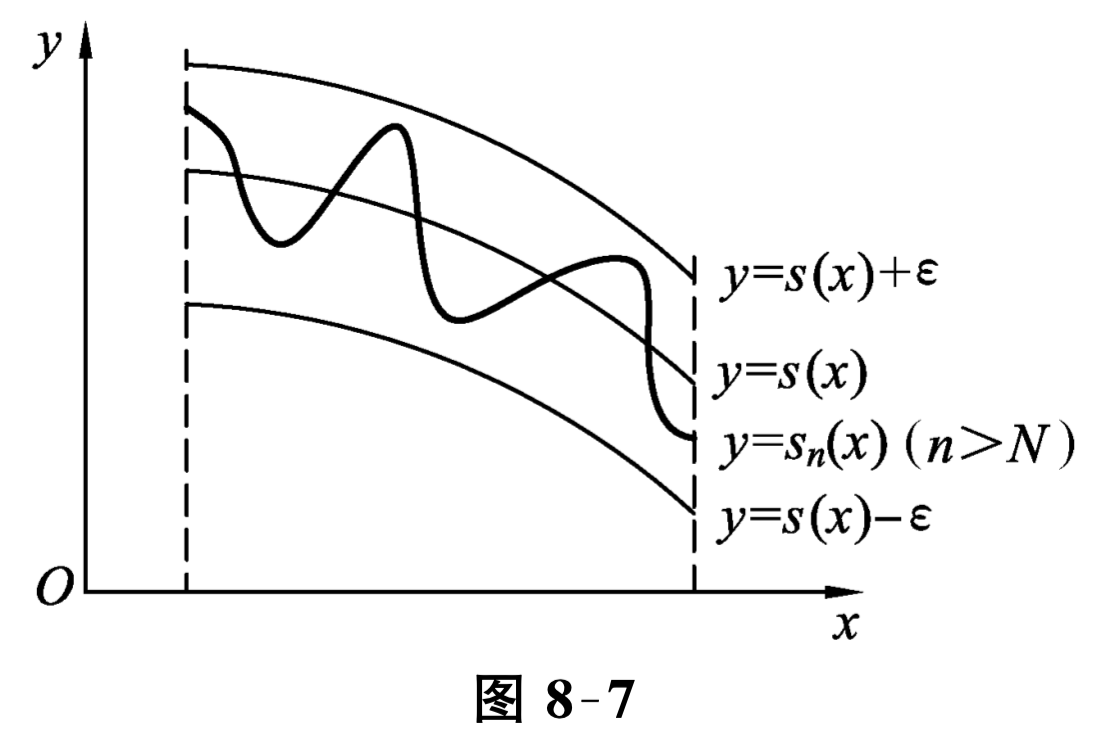
证 级数的部分和为
\begin{equation*}
s_{n}(x)=x+\left(x^{2}-x\right)+\cdots+\left(x^{n}-x^{n-1}\right)=x^{n},
\end{equation*}
当 \(-1<x<1\) 时, \(s_{n}(x)=x^{n} \rightarrow 0(n \rightarrow \infty)\text{,}\) 因此当 \(-1<x<1\) 时, 级数的和函数 \(s(x)=0\text{.}\)
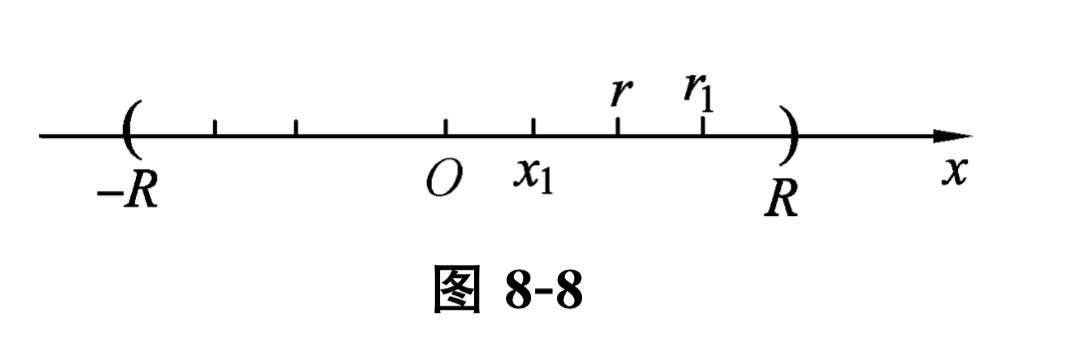
设 \([a, b]\) 为开区间 \((-1,1)\) 内任意闭子区间, 则 \(\max \{|a|,|b|\}<1\text{,}\) 所以存在 \(r\text{,}\) 使得 \(\max \{|a|,|b|\}<r<1\text{,}\) 从而 \([a, b] \subset[-r, r] \subset(-1,1)\text{.}\) 现在证明级数在 \([-r, r]\) 上一致收敛.
对于 \(|x| \leqslant r<1\) 的每一个 \(x\text{,}\) 要使得
\begin{equation*}
\left|s_{n}(x)-s(x)\right|=\left|x^{n}-0\right|=|x|^{n}<\varepsilon,
\end{equation*}
只要
\begin{equation*}
|x|^{n} \leqslant r^{n}<\varepsilon,
\end{equation*}
即
\begin{equation*}
n \ln r<\ln \varepsilon,
\end{equation*}
两边同除以 \(\ln r\text{,}\) 因为 \(\ln r<0\text{,}\) 所以只要 \(n>\frac{\ln \varepsilon}{\ln r}\text{.}\) 不妨限制 \(0<\varepsilon<1\text{,}\) 于是 \(\ln \varepsilon<0\text{,}\)即有 \(n>\frac{\ln \varepsilon}{\ln r}>0\text{.}\) 记 \(N=\left[\frac{\ln \varepsilon}{\ln r}\right]\text{,}\) 则当 \(n>N\) 时, 对 \(|x| \leqslant r<1\) 的每一个 \(x\text{,}\) 都有
\begin{equation*}
\left|s_{n}(x)-s(x)\right|=|x|^{n} \leqslant r^{n}<\varepsilon
\end{equation*}
成立. 显然这里的 \(N\) 与 \(x\) 无关,因此,级数在 \([-r, r]\) 上一致收敛.
因为 \([a, b]\) 是 \([-r, r]\) 的子区间,所以级数在 \([a, b]\) 也一致收敛. 已知 \([a, b]\) 是在 \((-1,1)\) 内任意给定的, 由此可知, 级数在 \((-1,1)\) 内内闭一致收敛.