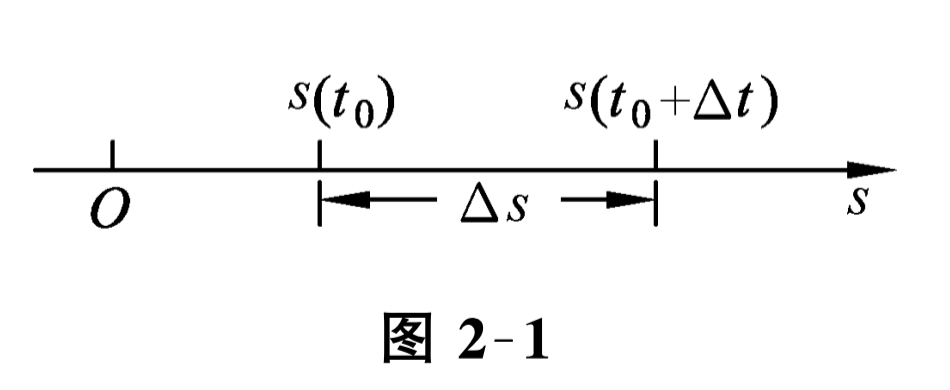Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 2.1 导数的概念

自文艺复兴以来,欧洲的工业、农业、航海业得到了大规模的发展,在资本主义生产力刺激下蓬勃发展的自然科学开始迈人综合与突破的阶段,而这种综合与突破所面临的数学困难使微积分学的基本问题空前地成为人们关注的焦点.
  1. 确定非匀速运动的速度与加速度, 即研究瞬时变化率问题;
  2. 望远镜的光程设计需要确定透镜曲面上任一点的法线, 并将其转化为求任意曲线的切线问题;
  3. 确定炮弹的最大射程及寻求行星轨道的近日点与远日点等都涉及函数极大值、极小值的问题.
这三类实际问题的现实原型在数学上都可归结为函数相对于自变量变化而变化的快慢程度, 即所谓函数的变化率问题. 牛顿从第一个问题出发, 莱布尼茨从第二个问题出发, 分别给出了导数的概念, 并导致了微积分学的诞生.

Subsection 2.1.1 引例

Subsubsection 2.1.1.1 变速直线运动的速度问题

对于匀速直线运动, 用距离除以时间就可得到该时间段内任一时刻的速度,但对于变速运动, 这种方法只能得到该时间段内的平均速度,那么如何求出在某个时刻的(瞬时) 速度呢?
设有一质点 \(M\) 做直线运动, 其运动规律为 \(s=s(t)\text{,}\) 当时间 \(t\) 从时刻 \(t_{0}\) 变到时刻 \(t_{0}+\Delta t\text{,}\) 位置函数 \(s\) 便由 \(s\left(t_{0}\right)\) 变到 \(s\left(t_{0}+\Delta t\right)\text{,}\) 即位置函数取得增量 \(\Delta s=s\left(t_{0}+\Delta t\right)-s\left(t_{0}\right)\) (见图 2-1).
把位置函数 \(s\) 的增量 \(\Delta s\) 与自变量时间 \(t\) 的增量 \(\Delta t\) 之比
\begin{equation*} \frac{\Delta s}{\Delta t}=\frac{s\left(t_{0}+\Delta t\right)-s\left(t_{0}\right)}{\Delta t} \end{equation*}
称为质点 \(M\) 在 \(\Delta t\) 这段时间内的平均速度, 记作 \(\bar{v}\text{,}\) 即
\begin{equation*} \bar{v}=\frac{\Delta s}{\Delta t}=\frac{s\left(t_{0}+\Delta t\right)-s\left(t_{0}\right)}{\Delta t} \end{equation*}
当质点 \(M\) 做匀速直线运动时, 平均速度 \(\bar{v}\) 就是 \(M\) 在 \(\Delta t\) 这段时间内各时刻的运动速度, 也是 \(M\) 在时刻 \(t=t_{0}\) 的 (瞬时) 速度. 当质点 \(M\) 做变速直线运动时, 平均速度只是质点 \(M\) 在时刻 \(t_{0}\) 的速度的近似值, 它不是 \(M\) 在时刻 \(t_{0}\) 的速度. 但当 \(|\Delta t|\) 很小时, 可以把平均速度近似地看作 \(t_{0}\) 时刻的瞬时速度, 而且 \(|\Delta t|\) 越小, 这种近似程度就越好. 当 \(\Delta t \rightarrow 0\) 时, 平均速度 \(\bar{v}=\frac{\Delta s}{\Delta t}\) 的极限就是质点 \(M\) 在 \(t_{0}\) 时刻的瞬时速度, 即
\begin{equation} v=\lim\limits_{\Delta t \rightarrow 0} \bar{v}=\lim\limits_{\Delta t \rightarrow 0} \frac{\Delta s}{\Delta t}=\lim\limits_{\Delta t \rightarrow 0} \frac{s\left(t_{0}+\Delta t\right)-s\left(t_{0}\right)}{\Delta t} .\tag{2.1.1} \end{equation}

Subsubsection 2.1.1.2 平面曲线的切线斜率问题

在初等数学中,圆的切线被定义为与圆只有一个交点的直线, 但对于一般曲线, 这样的定义显然是不合适的, 如图 2-2 中所给出的曲线 \(L\text{,}\) 直线 \(l_{1}\) 虽然和 \(L\)只有唯一交点, 但显然不能认为它与 \(L\) 相切; 而直线 \(l_{2}\) 与 \(L\) 的交点虽不止一个, 但它与 \(L\) 在点 \(A\) 处相切.因此, 在高等数学中, 切线是作为割线的极限位置来定义的.
设曲线 \(L\) 的方程为 \(y=f(x)\text{,}\) 如图 2-3 所示, 考虑曲线 \(L\) 上点 \(M_{0}\) 及附近的一点 \(M\text{,}\) 它们的坐标分别为 \(M_{0}\left(x_{0}, y_{0}\right)\) 与 \(M\left(x_{0}+\Delta x, y_{0}+\Delta y\right)\) (其中 \(\Delta x\) 可以大于 0 , 也可以小于 0 , 图中取 \(\Delta x\) 大于 0 ).
连接这两点的曲线 \(L\) 的割线 \(M_{0} M\text{,}\) 然后令点 \(M\) 沿着曲线 \(L\) 趋向 \(M_{0}\text{,}\) 这时割线 \(M_{0} M\)以 \(M_{0}\) 为中心沿曲线 \(L\) 转动, 当 \(M \rightarrow M_{0}\)时, 割线 \(M_{0} M\) 的极限位置 \(M_{0} T\) 称为曲线 \(L\) 在点 \(M_{0}\) 处的切线. 这里极限位置的含义是: 只要线段 \(M_{0} M\) 长度趋于零, \(\angle M M_{0} T\) 也趋于零.
求曲线 \(y=f(x)\) 的切线 \(M_{0} T\) 的方程关键就是求出它的斜率, 因为割线 \(M_{0} M\) 的斜率为
\begin{equation*} \bar{k}=\tan \varphi=\frac{\Delta y}{\Delta x}=\frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}, \end{equation*}
其中 \(\varphi\) 为割线 \(M_{0} M\) 的倾角. 当点 \(M\) 沿曲线 \(L\) 趋于点 \(M_{0}\) 时, \(\Delta x \rightarrow 0\text{,}\) 上式的极限值就是切线 \(M_{0} T\) 的斜率, 即切线 \(M_{0} T\) 的斜率为
\begin{equation} k=\tan \alpha=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x},\tag{2.1.2} \end{equation}
其中 \(\alpha\) 为切线 \(M_{0} T\) 的倾角.
Checkpoint 2.1.1. 练习题.
设点 \(P( 0.333333333333333 , 6 )\) 是曲线上 \(y = 2 / x\)一点 . 设 \(Q = (x, 2 / x ) .\)
a.) 对下述\(x\)的值，求割线 \(PQ\)的斜率.
若 \(x= 0.433333333333333\text{,}\) \(PQ\) 的斜率是:
若 \(x= 0.343333333333333\text{,}\) \(PQ\) 的斜率是:
若 \(x= 0.233333333333333\text{,}\) \(PQ\) 的斜率是:
若 \(x= 0.323333333333333\text{,}\) \(PQ\) 的斜率是:
b.) 基于上述计算，请猜测曲线在 \(P(0.333333333333333 , 6 )\)点处切线斜率.
Answer:

Subsubsection 2.1.1.3 细棒的线密度问题

假设有一质量分布非均匀的细棒, 放置在数轴 \(O l\)上, 其一端与原点 \(O\) 重合, 设细棒质量 \(m=m(l)\) (见图 2-4), 求它在 \(l_{0}\) 处的线密度.
∏ 考虑细棒长度从 \(l_{0}\) 取得增量 \(\Delta l\) 变到 \(l_{0}+\Delta l\) 时, 则细棒的质量 \(m\) 便相应地取得增量 \(\Delta m=m\left(l_{0}+\Delta l\right)-m\left(l_{0}\right)\text{.}\) 这段细棒的平均线密度
\begin{equation*} \bar{\rho}=\frac{\Delta m}{\Delta l}=\frac{m\left(l_{0}+\Delta l\right)-m\left(l_{0}\right)}{\Delta l} . \end{equation*}
当 \(l\) 的质量均匀分布时, \(\bar{\rho}\) 就是细棒在 \(\Delta l\) 这段长度内各点的线密度, 当细棒 \(l\)的质量非均匀分布时, \(\bar{\rho}\) 是细棒在 \(\Delta l\) 这段长度内各点线密度的近似值, 而且当 \(|\Delta l|\) 越小时, 近似程度越好. 因此, 当 \(\Delta l \rightarrow 0\) 时, 平均线密度 \(\bar{\rho}\) 的极限 \(\lim\limits_{\Delta l \rightarrow 0} \bar{\rho}=\) \(\lim\limits_{\Delta l \rightarrow 0} \frac{\Delta m}{\Delta l}\) 就是细棒在 \(l_{0}\) 点处的线密度, 记作 \(\rho\text{,}\) 即
\begin{equation} \rho=\lim\limits_{\Delta l \rightarrow 0} \bar{\rho}=\lim\limits_{\Delta l \rightarrow 0} \frac{\Delta m}{\Delta l}=\lim\limits_{\Delta l \rightarrow 0} \frac{m\left(l_{0}+\Delta l\right)-m\left(l_{0}\right)}{\Delta l} .\tag{2.1.3} \end{equation}
实际问题中还有很多类似的例子, 如电学中的电流强度 \(I\) 、热学中的比热容 \(c\) 、刚体转动中的角速度 \(\omega\) 等. 上述这些问题尽管各自的含义不同, 但解决它们的数学模型是相同的, 即都是求自变量的增量趋于零时, 函数的增量与自变量增量之比的极限. 抛开这些问题的具体含义, 只考虑它们的数学结构, 就抽象出导数的概念.

Subsection 2.1.2 导数的定义

Subsubsection 2.1.2.1 函数在一点处的导数

Definition 2.1.2.
设函数 \(y=f(x)\) 在 \(x_{0}\) 的某一邻域内有定义,而且当 \(x\) 在 \(x_{0}\) 取得增量 \(\Delta x\) 时 ( \(\Delta x \neq 0, x_{0}+\Delta x\) 仍在该邻域内), 相应地函数 \(y\) 有增量 \(\Delta y=f\left(x_{0}+\Delta x\right)-\) \(f\left(x_{0}\right)\text{.}\) 若当 \(\Delta x \rightarrow 0\) 时, \(\Delta y\) 与 \(\Delta x\) 之比 \(\frac{\Delta y}{\Delta x}\) 的极限存在, 则称函数 \(f(x)\) 在点 \(x_{0}\)处可导, 并称此极限值为函数 \(y=f(x)\) 在点 \(x_{0}\) 处的导数, 记作
\begin{equation} f^{\prime}\left(x_{0}\right)=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x},\tag{2.1.4} \end{equation}
也可以记作
\begin{equation*} \left.y^{\prime}\right|_{x=x_{0}},\left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{x=x_{0}} \text { 或 }\left.\frac{\mathrm{d} f(x)}{\mathrm{d} x}\right|_{x=x_{0}} . \end{equation*}
若(2.1.4) 中极限不存在, 则称函数 \(f(x)\) 在点 \(x_{0}\) 处不可导. 若(2.1.4)中的极限为无穷大, 虽然导数不存在, 但为了方便, 也说 \(f(x)\) 在 \(x_{0}\) 处的导数为无穷大, 记作 \(f^{\prime}\left(x_{0}\right)=\infty\text{.}\)

Subsubsection 2.1.2.2 关于导数定义的几点说明

  1. 函数在点 \(x_{0}\) 处的导数是因变量在点 \(x_{0}\) 处的变化率, 它反映了因变量随自变量的变化而变化的快慢程度.
  2. 导数的定义(2.1.4) 有以下常用的等价形式: 若令 \(\Delta x=h\text{,}\) 则有
    \begin{equation} f^{\prime}\left(x_{0}\right)=\lim\limits_{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h} .\tag{2.1.5} \end{equation}
    若令 \(x=x_{0}+\Delta x\text{,}\) 则 \(\Delta x=x-x_{0}\text{,}\) 当 \(\Delta x \rightarrow 0\) 时 \(x \rightarrow x_{0}\text{,}\) 这时(2.1.4) 就变成
    \begin{equation} f^{\prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}\tag{2.1.6} \end{equation}
    由于上式右端的分母 、分子分别是 \(x\) 与 \(x_{0}\) 处自变量值的差及其函数值的差,所以
    \begin{equation*} \frac{\Delta y}{\Delta x}=\frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \end{equation*}
    也称为差商, 因此导数就是差商的极限.
  3. 按照导数的定义,变速直线运动物体的速度是位置函数 \(s=s(t)\) 对于时间 \(t\) 的导数, 即 \(v=\frac{\mathrm{d} s}{\mathrm{~d} t}\text{;}\) 曲线 \(y=f(x)\) 在点 \((x, f(x))\) 处切线的斜率就是函数 \(y=f(x)\)对于自变量 \(x\) 的导数, 即 \(k=\tan \alpha=\frac{\mathrm{d} y}{\mathrm{~d} x}\text{;}\) 细棒的线密度就是质量分布函数 \(m=\) \(m(l)\) 对于长度 \(l\) 的导数, 即 \(\rho=\frac{\mathrm{d} m}{\mathrm{~d} l}\text{.}\)
  4. 求导步骤.
    由定义知道, 求函数 \(y=f(x)\) 点 \(x_{0}\) 处的导数的一般步骤如下:
    第一步,根据自变量的增量求函数的增量 \(\Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)\text{;}\)
    第二步,求函数增量与自变量增量的比式 \(\frac{\Delta y}{\Delta x}=\frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}\text{;}\)
    第三步, 求当 \(\Delta x \rightarrow 0\) 时函数增量与自变量增量比式的极限, 即
    \begin{equation*} f^{\prime}\left(x_{0}\right)=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} . \end{equation*}

Subsubsection 2.1.2.3 单侧导数

导数是比值 \(\frac{\Delta y}{\Delta x}\) 当 \(\Delta x \rightarrow 0\) 时的极限, 比照左、右极限的概念, 自然地, 如果 \(\lim\limits_{\Delta x \rightarrow 0^{-}} \frac{\Delta y}{\Delta x}\) 与 \(\lim\limits_{\Delta x \rightarrow 0^{+}} \frac{\Delta y}{\Delta x}\) 存在, 那么分别称它们为函数 \(f(x)\) 在点 \(x_{0}\) 处的左导数与右导数, 分别记为 \(f_{-}^{\prime}\left(x_{0}\right)\) 与 \(f_{+}^{\prime}\left(x_{0}\right)\text{,}\) 即
\begin{align} f_{-}^{\prime}\left(x_{0}\right)\amp=\lim\limits_{\Delta x \rightarrow 0^{-}} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x},\tag{2.1.7}\\ f_{+}^{\prime}\left(x_{0}\right)\amp=\lim\limits_{\Delta x \rightarrow 0^{+}} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} .\tag{2.1.8} \end{align}
根据左、右极限的性质, 我们有以下定理.
单侧导数的概念在求分段函数在分段点处的导数时会用到. 若函数 \(f(x)\) 在开区间 \((a, b)\) 内每一点都可导, 则称 \(f(x)\) 在 \((a, b)\) 内可导. 如果 \(f(x)\) 在 \((a, b)\) 内可导, 且 \(f_{+}^{\prime}(a), f_{-}^{\prime}(b)\) 存在, 则称函数 \(f(x)\) 在闭区间 \([a, b]\) 上可导.

Subsubsection 2.1.2.4 导函数

若函数 \(y=f(x)\) 在区间 \(I\) 上每一点都可导, 则称 \(y=f(x)\) 在区间 \(I\) 上可导, 这时对于 \(I\) 上任一点 \(x\text{,}\) 都对应着一个确定的导数 \(f^{\prime}(x)\text{,}\) 这样就构成一个新的函数, 称为函数 \(y=f(x)\) 的导函数, 记作 \(f^{\prime}(x)\) 或 \(\frac{\mathrm{d} y}{\mathrm{~d} x}\) 或 \(y^{\prime}\) 或 \(\frac{\mathrm{d} f(x)}{\mathrm{d} x}\text{,}\) 即
\begin{equation} f^{\prime}(x)=\lim\limits_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\tag{2.1.9} \end{equation}
比较(2.1.4) 与(2.1.9) 可知, 导函数 \(f^{\prime}(x)\) 在点 \(x_{0}\) 处的值就是函数 \(y=f(x)\) 在点 \(x_{0}\) 处的导数 \(f^{\prime}\left(x_{0}\right)\text{,}\) 即
\begin{equation*} f^{\prime}\left(x_{0}\right)=\left.f^{\prime}(x)\right|_{x=x_{0}} \end{equation*}
一般将导函数简称为导数.
Example 2.1.4.
例 1 已知自由落体的运动方程为 \(s=\frac{1}{2} g t^{2}\text{,}\) 求:
  1. 落体在 \(t_{0}\) 到 \(t\) 这段时间内的平均速度及当 \(t_{0}=10 \mathrm{~s}, \Delta t=0.1 \mathrm{~s}\) 时的平均速度.
  2. 落体在 \(t=t_{0}\) 时的瞬时速度及当 \(t_{0}=10 \mathrm{~s}\) 时的瞬时速度.
Solution.
解 (1) 当 \(t\) 从 \(t=t_{0}\) 变到 \(t=t_{0}+\Delta t\) 时, 自由落体移动的路程为
\begin{equation*} \Delta s=\frac{1}{2} g\left(t_{0}+\Delta t\right)^{2}-\frac{1}{2} g t_{0}^{2} . \end{equation*}
在 \(\Delta t=\left(t_{0}+\Delta t\right)-t_{0}\) 这段时间内平均速度为
\begin{equation*} \bar{v}=\frac{\Delta s}{\Delta t}=\frac{\frac{1}{2} g\left[\left(t_{0}+\Delta t\right)^{2}-t_{0}^{2}\right]}{\Delta t}=g\left(t_{0}+\frac{1}{2} \Delta t\right), \end{equation*}
当 \(t_{0}=10 \mathrm{~s}, \Delta t=0.1 \mathrm{~s}\) 时, \(\bar{v}=g(10+0.05)=10.05 \mathrm{~g} \mathrm{~m} / \mathrm{s}\text{.}\)
  1. 落体在 \(t=t_{0}\) 时的瞬时速度为
\begin{equation*} v=\lim\limits_{\Delta t \rightarrow 0} \bar{v}=\lim\limits_{\Delta t \rightarrow 0} g\left(t_{0}+\frac{1}{2} \Delta t\right)=g t_{0}, \end{equation*}
当 \(t_{0}=10 \mathrm{~s}\) 时, 落体的瞬时速度为 \(v=10 \mathrm{~g} \mathrm{~m} / \mathrm{s}\text{.}\)
Example 2.1.5.
例 2 讨论函数 \(y=f(x)=|x|\) 在 \(x=0\) 处的可导性.
Solution.
解
\begin{equation*} f(x)=|x|= \begin{cases}x, & x \geqslant 0, \\ -x, & x<0 .\end{cases} \end{equation*}
\begin{equation*} \begin{aligned} & f_{+}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{+}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{+}} \frac{x}{x}=1, \\ & f_{-}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{-}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{-}} \frac{-x}{x}=-1 . \end{aligned} \end{equation*}
由于 \(f_{+}^{\prime}(0) \neq f_{-}^{\prime}(0)\text{,}\) 故 \(f(x)\) 在 \(x=0\) 不可导, 如 图 2-5 所示,在 \(x=0\) 处 \(f(x)\) 图像有一尖点.

Subsubsection 2.1.2.5 几个简单函数的导数

利用导数的定义,求出下列几个函数的导数.
Example 2.1.6.
例 3 求函数 \(y=C\) ( \(C\) 为常数) 的导数.
Solution.
解 \(y^{\prime}=\lim\limits_{\Delta x \rightarrow 0} \frac{C-C}{\Delta x}=0\text{,}\) 即
\begin{equation*} (C)^{\prime}=0 \text {. } \end{equation*}
Example 2.1.7.
例 4 求函数 \(y=\frac{1}{x}(x \neq 0)\) 在点 \(-1, \frac{1}{2}, 1\) 处的导数.
Solution.
解 \(y^{\prime}=\lim\limits_{\Delta x \rightarrow 0} \frac{\frac{1}{x+\Delta x}-\frac{1}{x}}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{-1}{x(x+\Delta x)}=-\frac{1}{x^{2}}\text{,}\) 即
\begin{equation*} \left(\frac{1}{x}\right)^{\prime}=-\frac{1}{x^{2}} \end{equation*}
因此, \(\left.y^{\prime}\right|_{x=-1}=-1,\left.y^{\prime}\right|_{x=\frac{1}{2}}=-4,\left.y^{\prime}\right|_{x=1}=-1\text{.}\)
Example 2.1.8.
例 5 求函数 \(y=x^{n}\) ( \(n\) 为正整数) 在 \(x_{0}\) 处的导数.
Solution.
\begin{equation*} \begin{aligned} y^{\prime} &=\lim\limits_{\Delta x \rightarrow 0} \frac{\left(x_{0}+\Delta x\right)^{n}-x_{0}^{n}}{\Delta x}\\ & =\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta x\left[\left(x_{0}+\Delta x\right)^{n-1}+\left(x_{0}+\Delta x\right)^{n-2} x_{0}+\cdots+x_{0}^{n-1}\right]}{\Delta x} \\ & =n x_{0}^{n-1} . \end{aligned} \end{equation*}
由 \(x_{0}\) 的任意性,对任意 \(x \in(-\infty,+\infty)\text{,}\) 都有
\begin{equation*} \left(x^{n}\right)^{\prime}=n x^{n-1} . \end{equation*}
可以证明: 当 \(x \neq 0, n\) 为任何实数时, 上式仍成立; 如当 \(n=-1\) 时, \(\left(\frac{1}{x}\right)^{\prime}=\) \((-1) x^{-2}=-\frac{1}{x^{2}}\text{,}\) 这就是Example 2.1.7 的结果.

Subsection 2.1.3 导数的几何意义

由 Subsubsection 2.1.1.2 与导数的定义可知, 函数 \(y=f(x)\) 在点 \(x_{0}\) 处的导数, 就是曲线 \(y=f(x)\) 在点 \(M_{0}\left(x_{0}, f\left(x_{0}\right)\right.\) ) 处的切线 \(M_{0} T\) 的斜率 (见图 2-3), 即
\begin{equation*} k=\tan \alpha=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=f^{\prime}\left(x_{0}\right) . \end{equation*}
由此可得曲线 \(y=f(x)\) 在 \(M_{0}\) 点处的切线方程为
\begin{equation} y-f\left(x_{0}\right)=f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\tag{2.1.10} \end{equation}
过切点与切线垂直的直线称为曲线在该点的法线. 过 \(M_{0}\) 点的法线方程为
\begin{equation} y-f\left(x_{0}\right)=-\frac{1}{f^{\prime}\left(x_{0}\right)}\left(x-x_{0}\right)\left(f^{\prime}\left(x_{0}\right) \neq 0\right)\tag{2.1.11} \end{equation}

Example 2.1.9.

例 6 求曲线 \(y=\frac{1}{x^{2}}\) 在点 \(M_{0}\left(2, \frac{1}{4}\right)\) 处的切线方程与法线方程.
Solution.
解 \(y^{\prime}=-2 x^{-3}=-\frac{2}{x^{3}},\left.y^{\prime}\right|_{x=2}=-\frac{1}{4}\text{.}\) 过 \(M_{0}\) 的切线方程为
\begin{equation*} y-\frac{1}{4}=-\frac{1}{4}(x-2), \end{equation*}
即
\begin{equation*} x+4 y-3=0 . \end{equation*}
过 \(M_{0}\) 的法线方程为
\begin{equation*} y-\frac{1}{4}=4(x-2), \end{equation*}
即
\begin{equation*} 16 x-4 y-31=0 \text {. } \end{equation*}

Example 2.1.10.

例 7 求曲线 \(y=\sqrt[3]{x}\) 在点 \(O(0,0)\) 处的切线方程.
Solution.
解 \(f^{\prime}(0)=\lim\limits_{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{\sqrt[3]{\Delta x}-0}{\Delta x}\)
\begin{equation*} =\lim\limits_{\Delta x \rightarrow 0} \frac{1}{\sqrt[3]{(\Delta x)^{2}}}=+\infty \end{equation*}
可见 \(y=\sqrt[3]{x}\) 在 \(x=0\) 处不可导或导数为 \(\infty\text{,}\) 曲线在 \(O(0,0)\) 处切线斜率为 \(\infty\text{,}\) 即曲线 \(y=\sqrt[3]{x}\) 在 \(O(0,0)\) 处的切线与 \(x\) 轴垂直, 就是 \(y\) 轴, 故切线方程为 \(x=0\text{.}\) 从而曲线 \(y=\sqrt[3]{x}\) 在 \(O(0,0)\) 的法线方程为 \(y=0\text{,}\) 即 \(x\) 轴 (见图 2-6).

Example 2.1.11.

例 8 求与直线 \(x+9 y-1=0\) 垂直的曲线 \(y=x^{3}-3 x^{2}+5\) 的切线方程.
Solution.
解 因为曲线 \(y=x^{3}-3 x^{2}+5\) 上任一点处切线的斜率为 \(y^{\prime}=3 x^{2}-6 x\text{.}\) 而直线 \(x+9 y-1=0\) 的斜率为 \(-\frac{1}{9}\text{,}\) 依题意知 \(3 x^{2}-6 x=9\text{,}\) 解得 \(x_{1}=-1, x_{2}=3\text{.}\) 故切点为 \((-1,1)\) 或 \((3,5)\text{,}\) 两切点的切线斜率分别为 \(k_{1}=\left.y^{\prime}\right|_{x=-1}=9\text{,}\) \(k_{2}=\left.y^{\prime}\right|_{x=3}=9\text{.}\) 两切线方程为 即
\begin{equation*} y-1=9(x+1), y-5=9(x-3), \end{equation*}
\begin{equation*} y-9 x-10=0, y-9 x+22=0 \text {. } \end{equation*}

Subsection 2.1.4 利用单位解释导数

假设 \(s=f(t)\) 为在 \(t\) 时刻物体离一个固定点的位置函数, \(s\) 的单位为 \(\mathrm{m}, t\) 的单位为 \(\mathrm{s}\text{,}\) 那么 \(\frac{\mathrm{d} s}{\mathrm{~d} t}=f^{\prime}(2)=10 \mathrm{~m} / \mathrm{s}\) 表明在 \(t=2 \mathrm{~s}\) 时物体正以 \(10 \mathrm{~m} / \mathrm{s}\) 的速度运动.如果该物体继续以这一速度运动 \(1 \mathrm{~s}\) (从 \(t=2\) 到 \(t=3\) ), 那么物体就会又移动 \(10 \mathrm{~m}\)左右. 一般地有以下关系:
  1. 函数的导数单位为因变量的单位除以自变量的单位;
  2. 如果一个函数的导数在某一点附近不是剧烈变化的, 那么函数在该点的导数近似地等于自变量增加一个单位时函数的变化量.

Example 2.1.12.

例 9 建一栋 \(A \mathrm{~m}^{2}\) 房子的成本函数为 \(C=f(A)\) (单位: 元). 函数 \(f^{\prime}(A)\) 的实际意义是什么?
Solution.
解 \(f^{\prime}(A)=\frac{\mathrm{d} C}{\mathrm{~d} A}\) 是成本除以面积, 故它可以用“元 \(/ \mathrm{m}^{2}\) ” 来计量. 若将 \(\mathrm{d} C\) 看成建造完成后另外增加 \(\mathrm{d} A\) 所需增加的成本, 则 \(\frac{\mathrm{d} C}{\mathrm{~d} A}\) 是每平方米的追加成本. 因此, 如果计划建一栋面积约为 \(A\) 的房子, 那么 \(f^{\prime}(A)\) 就是建造稍大一点房子的每平方米增加面积的成本.

Example 2.1.13.

例 10 从一个矿井中采 \(T \mathrm{t}\) 铜矿石的成本 \(C=f(T)\) 元, 则 \(f^{\prime}(2000)=1000\)的含义是什么?
Solution.
解
\begin{equation*} f^{\prime}(2000)=\left.\frac{\mathrm{d} C}{\mathrm{~d} T}\right|_{T=2000} \end{equation*}
因为 \(C\) 的计量单位是元, 而 \(T\) 的计量单位是 \(\mathrm{t}\text{,}\) 那么 \(\frac{\mathrm{d} C}{\mathrm{~d} T}\) 的计量单位应该是 “元/ \(\mathrm{t}\)”. 所以 \(\left.\frac{\mathrm{d} C}{\mathrm{~d} T}\right|_{T=2000}=1000\) 表明矿井中已经采得 \(2000 \mathrm{t}\) 矿石时,再采下 \(1 \mathrm{t}\)矿石的成本近似为 1000 元. 换句话说, 采第 \(2001 \mathrm{t}\) 矿石的成本大约是 1000 元.

Example 2.1.14.

例 11 已知在一个管道中水以 \(10 \mathrm{~m}^{3} / \mathrm{s}\) 的速度流动. 试以某个函数的导数解释这个速度.
Solution.
解 事实上 \(10 \mathrm{~m}^{3} / \mathrm{s}\) 的水流速度可能是流动非常缓慢的水通过一个较大的管道所达到的, 也可能是流动非常迅速的水通过一个较窄的管道所达到的. 如果考察它的单位- \(\mathrm{m}^{3} / \mathrm{s}\text{,}\) 就会发现它是以立方米计量的某量的变化率. 而立方米是体积的计量单位, 所以该单位是体积的变化率. 设想所有流动的水最终流进了水箱的某个地方, 并且设 \(V(t)\) 表示 \(t\) 时刻水箱中水的体积, 那么可得 \(V(t)\) 的变化率为 10 , 即 \(V^{\prime}(t)=\frac{\mathrm{d} V}{\mathrm{~d} t}=10\text{.}\)

Subsection 2.1.5 函数的可导性与连续性的关系

若函数 \(f(x)\) 在点 \(x_{0}\) 可导, 即 \(f^{\prime}\left(x_{0}\right)\) 存在, 由 \(f^{\prime}\left(x_{0}\right)=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}\text{,}\) 得 \(\frac{\Delta y}{\Delta x}=\) \(f^{\prime}\left(x_{0}\right)+\alpha\text{,}\) 其中 \(\lim\limits_{\Delta x \rightarrow 0} \alpha=0\text{,}\) 则
\begin{equation} \Delta y =f'(x_0)\Delta x +\alpha \Delta x,\tag{2.1.12} \end{equation}
从而
\begin{equation*} \lim\limits_{\Delta x \rightarrow 0} \Delta y=\lim\limits_{\Delta x \rightarrow 0}[f^{\prime}\left(x_{0}\right) \Delta x+\alpha \Delta x]=0, \end{equation*}
即 \(f(x)\) 在 \(x_{0}\) 连续. 因此, 我们有如下结论:
若函数 \(f(x)\) 在点 \(x_{0}\) 可导, 则 \(f(x)\) 在点 \(x_{0}\) 必定连续.
但上述命题的逆命题不成立, 由Example 2.1.5可知, 函数 \(y=|x|\) 在 \(x=0\) 处连续,但在 \(x=0\)处不可导; 又如Example 2.1.10 中函数 \(y=\sqrt[3]{x}\) 在 \(x=0\) 处连续,但在 \(x=0\) 处不可导.

Example 2.1.15.

例 12 讨论函数 \(f(x)=\left\{\begin{array}{ll}x \sin \frac{1}{x}, & x \neq 0, \\ 0, & x=0\end{array}\right.\) 在 \(x=0\) 处的可导性.
Solution.
解 因为 \(\lim\limits_{x \rightarrow 0} f(x)=\lim\limits_{x \rightarrow 0}\left(x \sin \frac{1}{x}\right)=0=f(0)\text{,}\) 所以 \(f(x)\) 在 \(x=0\) 处连续. 而 \(\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta x \sin \frac{1}{\Delta x}-0}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \sin \frac{1}{\Delta x}\) 不存在, 故 \(f(x)\) 在 \(x=0\) 处不可导.

Example 2.1.16.

例 13 设函数 \(f(x)=\left\{\begin{array}{ll}a, & x<0, \\ x^{2}+1, & 0 \leqslant x<1,\end{array}\right.\) 问 \(a\) 取何值时 \(f(x)\) 为可导函数.
Solution.
解 当 \(x<0\) 时, \(f(x)=a\) 是处处可导的. 当 \(0<x<1\) 时, \(f(x)=x^{2}+1\) 也是处处可导的. 因此,只需讨论在 \(x=0\) 处 \(f(x)\) 可导时 \(a\) 的取值情况. 在 \(x=0\) 处, 因为
\begin{equation*} \begin{gathered} f_{-}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{-}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{-}} \frac{a-1}{x}, \\ f_{+}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{+}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{+}} \frac{x^{2}+1-1}{x}=0, \end{gathered} \end{equation*}
要使 \(f(x)\) 在 \(x=0\) 处可导, 必须 \(\lim\limits_{x \rightarrow 0^{-}} \frac{a-1}{x}=0\text{,}\) 解得 \(a=1\text{.}\) 所以当 \(a=1\) 时 \(f(x)\) 为可导函数.

Example 2.1.17.

例 14 设函数 \(f(x)= \begin{cases}2 \mathrm{e}^{x}+a, & x<0, \\ x^{2}+b x+1, & x \geqslant 0 .\end{cases}\)
  1. 欲使 \(f(x)\) 在 \(x=0\) 处连续, \(a, b\) 为何值?
  2. 欲使 \(f(x)\) 在 \(x=0\) 处可导, \(a, b\) 为何值?
Solution.
解 (1) 若 \(f(x)\) 在 \(x=0\) 处连续, 则有
\begin{equation*} \lim\limits_{x \rightarrow 0^{-}} f(x)=\lim\limits_{x \rightarrow 0^{+}} f(x)=f(0)=1 \text {, 即 } 2+a=1 \text {, 解得 } a=-1 \text {. } \end{equation*}
所以当 \(a=-1, b\) 为任何实数时 \(f(x)\) 在 \(x=0\) 处连续.
  1. 若 \(f(x)\) 在 \(x=0\) 处可导,则有
\begin{equation*} \begin{aligned} & f_{-}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{-}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{-}} \frac{2 \mathrm{e}^{x}-2}{x}=2(\text { 因为 } a=-1), \\ & f_{+}^{\prime}(0)=\lim\limits_{x \rightarrow 0^{+}} \frac{f(x)-f(0)}{x-0}=\lim\limits_{x \rightarrow 0^{+}} \frac{x^{2}+b x+1-1}{x}=b . \end{aligned} \end{equation*}
由 \(f_{+}^{\prime}(0)=f_{-}^{\prime}(0)\) 得 \(b=2\text{,}\) 所以 \(a=-1, b=2\) 时 \(f(x)\) 在 \(x=0\) 处可导.

Subsection 2.1.6 导数在自然学科中的应用实例

Subsubsection 2.1.6.1 光栅的色散

光栅是光学中用于测定光谱线波长的仪器, 投在光栅上人射光的每一个波长 \(\lambda\) 都有相应确定的偏转角 \(\theta\text{,}\) 因此偏转角是波长 \(\lambda\) 的函数. 当波长由 \(\lambda\) 变为 \(\lambda+\Delta \lambda\text{,}\)偏转角的平均变化率为
\begin{equation*} \frac{\Delta \theta}{\Delta \lambda}=\frac{\theta(\lambda+\Delta \lambda)-\theta(\lambda)}{\Delta \lambda}, \end{equation*}
而在波长 \(\lambda\) 处的偏转角变化率
\begin{equation*} \frac{\mathrm{d} \theta}{\mathrm{d} \lambda}=\lim\limits_{\Delta \lambda \rightarrow 0} \frac{\Delta \theta}{\Delta \lambda} \end{equation*}
称为光栅的色散.

Subsubsection 2.1.6.2 气体的压缩与压缩系数

温度恒定的气体体积 \(V\) 是随压强 \(p\) 变化的, 当压强由 \(p\) 增至 \(p+\Delta p\) 时, 相应的体积的增量为 \(\Delta V=V(p+\Delta p)-V(p)\text{,}\) 体积平均增长率为
\begin{equation*} \frac{\Delta V}{\Delta p}=\frac{V(p+\Delta p)-V(p)}{\Delta p} . \end{equation*}
当 \(\Delta p>0\) 时, 显然有 \(\Delta V \leqslant 0\text{,}\) 因此上述比值非正, 从而其绝对值反映体积对压强的平均压缩率.
\begin{equation*} \frac{\mathrm{d} V}{\mathrm{~d} p}=\lim\limits_{\Delta p \rightarrow 0} \frac{\Delta V}{\Delta p} \end{equation*}
是压强为 \(p\) 时体积的压缩率. 热力学中定义
\begin{equation*} \beta=-\frac{V(p)}{V} \end{equation*}
为气体的等温压缩系数, 它反映了压强为 \(p\) 时单位体积气体的体积压缩率.

Subsubsection 2.1.6.3 生物种群的增长率

设 \(N=N(t)\) 表示某生物种群在时刻 \(t\) 的个体总数, 则从 \(t\) 到 \(t+\Delta t\) 这段时间间隔内种群的平均增长率定义为
\begin{equation*} \frac{\Delta N}{\Delta t}=\frac{N(t+\Delta t)-N(t)}{\Delta t} . \end{equation*}
为了研究该种群个体数量的变化规律, 需要得到在任意时刻 \(N\) 对时间的变化率, 即
\begin{equation*} \frac{\mathrm{d} N}{\mathrm{~d} t}=\lim\limits_{\Delta t \rightarrow 0} \frac{\Delta N}{\Delta t}, \end{equation*}
它在生物学中称为种群的增长率. 当然种群个体总数 \(N(t)\) 只能取正整数, 是不连续的函数, 因而它也不可导. 但由于多数生物种群的繁衍是世代延续, 其数量庞大, 当时间间隔 \(\Delta t\) 较小时, 由出生和死亡引起的种群个体数量的变化相对于个体总数来说也较小,故可近似地把 \(N(t)\) 看成连续可导函数. 事实上, 以 \(N^{\prime}(t)\) 作为增长率已经在研究物种增长及相关问题中发挥了重要作用.

Subsection 2.1.7 第一节知识图谱

Figure 2.1.18. 第一节知识图谱

Subsection 2.1.8 习题

  1. 一物体从 \(400 \mathrm{~m}\) 的高空下落, 它下落时刻 \(t\) (单位: \(\mathrm{s}\) ) 时距地面的高度是
    \begin{equation*} h=-16 t^{2}+400(\mathrm{~m}). \end{equation*}
    1. 求在前 \(4 \mathrm{~s}\) 内物体下落的平均速度;
    2. 求在第 \(4 \mathrm{~s}\) 时物体下落的瞬时速度.
  2. 求下列曲线在指定点处的切线斜率与切线方程:
    1. \(y=x^{3}+1\) 在点 \((1,2)\) 处;
    2. \(y=\sqrt{x}\) 在点 \((1,1)\) 处.
  3. 在做等速旋转时, 角速度是旋转角度与所耗时间之比, 已知非匀速旋转时, 旋转角 \(\omega\) 与时间 \(t\) 有如下关系: \(\omega=\omega(t)\text{,}\) 试导出非匀速旋转时的角速度表达式.
  4. 利用导数定义求下列函数在指定点 \(x_{0}\) 处的导数：
    1. \(f(x)=\frac{1}{x^{2}}, x_{0}=2\text{;}\)
    2. \(f(x)=\frac{1}{\sqrt{x}}, x_{0}=2\text{;}\)
    3. \(\displaystyle f(x)= \begin{cases}x^{2} \sin \frac{1}{x}, & x \neq 0, \\ 0, & x=0,\end{cases}\)
  5. 求下列函数在分段点处的左右导数, 指出函数在该点的可导性:
    1. \(\displaystyle y= \begin{cases}x, & x \geqslant 0, \\ x^{3}, & x<0 ;\end{cases}\)
    2. \(\displaystyle y= \begin{cases}x, & x \geqslant 0, \\ \sin x, & x<0 ;\end{cases}\)
    3. \(\displaystyle y= \begin{cases}\mathrm{e}^{x}-1, & x \geqslant 0, \\ x-x^{2}, & x<0 .\end{cases}\)
  6. 设 \(f(x)=\left\{\begin{array}{ll}x^{2}+a, & x \geqslant 1, \\ b x+1, & x<1 .\end{array}\right.\) 问 \(a, b\) 为何值时, \(f(x)\) 在 \(x=1\) 处可导?
  7. 设 \(f(x)=\left\{\begin{array}{ll}x^{\alpha} \sin \frac{1}{x}, & x \neq 0, \\ 0, & x=0,\end{array}\right.\) 讨论当 \(\alpha\) 为何值时, \(f(x)\) 在 \(x=0\) 处：(1) 连续; (2) 可导; (3) 导函数连续.
  8. 设 \(f^{\prime}\left(x_{0}\right)\) 存在, 求下列极限:
    \begin{equation*} \begin{aligned} & \text { (1) } \lim\limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}-\Delta x\right)-f\left(x_{0}\right)}{\Delta x} \text {; } \\ & \text { (2) } \lim\limits_{h \rightarrow 0} \frac{f\left(x_{0}\right)-f\left(x_{0}-2 h\right)}{h} \text {; }\\ & \text {(3)} \lim\limits_{h \rightarrow 0} \frac{f\left(x_{0}+2 h\right)-f\left(x_{0}-3 h\right)}{h}. \end{aligned} \end{equation*}
  9. 曲线 \(y=x^{3}\) 上哪一点的切线平行于直线 \(y-12 x-1=0\) ? 哪一点的法线平行于直线 \(y+12 x-1=0\) ?
  10. 设曲线 \(L: y=\sin x, x \in(-\infty,+\infty)\text{,}\)
    1. 求曲线 \(L\) 在原点处的切线方程与法线方程;
    2. 写出曲线 \(L\) 的水平切线方程及其与曲线的无穷多个交点的坐标.
  11. 从水箱开始放水 \(t \min\) 后, 水箱中剩余的水由 \(Q(t)=200(30-t)^{2}\) 表示 (单位: \(\mathrm{L}\) ), 则 \(10 \mathrm{~min}\) 刚过时水流有多快? 在刚开始 \(10 \mathrm{~min}\) 里水流出的平均流出率为多少?
PrevTopNext