Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 1.2 极限

极限是研究变量的变化趋势的基本工具, 高等数学中许多基本概念, 如连续、导数、定积分、无穷级数等都是建立在极限的基础上. 极限方法是研究函数的一种最基本的方法.

Subsection 1.2.1 数列的极限及其性质

Subsubsection 1.2.1.1 数列的概念

一个以正整数集 \(\mathbf{N}_{+}\)为定义域的函数 \(y=f(n)\text{,}\) 当自变量 \(n\) 按正整数 1,2 , \(3, \cdots, n, \cdots\) 增大的顺序依次取值时, 所得到的一串有序的函数值 \(f(1), f(2), \cdots\text{,}\) \(f(n), \cdots\) 称为数列, 记作 \(f(n), n=1,2,3, \cdots\text{.}\) 习惯上, 常把 \(f(n)\) 记作 \(x_{n}\text{,}\) 即 \(x_{n}=f(n)\text{,}\) 从而数列可记为
\begin{equation*} x_{1}, x_{2}, x_{3}, \cdots, x_{n}, \cdots, \end{equation*}
简记为 \(\left\{x_{n}\right\}, x_{n}\) 称为数列的第 \(n\) 项或通项, \(n\) 称为 \(x_{n}\) 的下标. 例如:
\begin{equation*} \begin{aligned} & \left\{\frac{1}{n}\right\}: 1, \frac{1}{2}, \frac{1}{3}, \cdots, \frac{1}{n}, \cdots ; \\ & \left\{(-1)^{n+1} \frac{1}{n}\right\}: 1,-\frac{1}{2}, \frac{1}{3},-\frac{1}{4}, \cdots,(-1)^{n+1} \frac{1}{n}, \cdots ; \\ & \left\{\frac{n}{n+1}\right\}: \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \cdots, \frac{n}{n+1}, \cdots ; \\ & \left\{\frac{2 n+(-1)^{n+1}}{n}\right\}: 3, \frac{3}{2}, \frac{7}{3}, \cdots, \frac{2 n+(-1)^{n+1}}{n}, \cdots ; \\ & \left\{n^{3}\right\}: 1,8,27, \cdots, n^{3}, \cdots ; \\ & \left\{(-1)^{n+1}\right\}: 1,-1,1, \cdots,(-1)^{n+1}, \cdots . \end{aligned} \end{equation*}
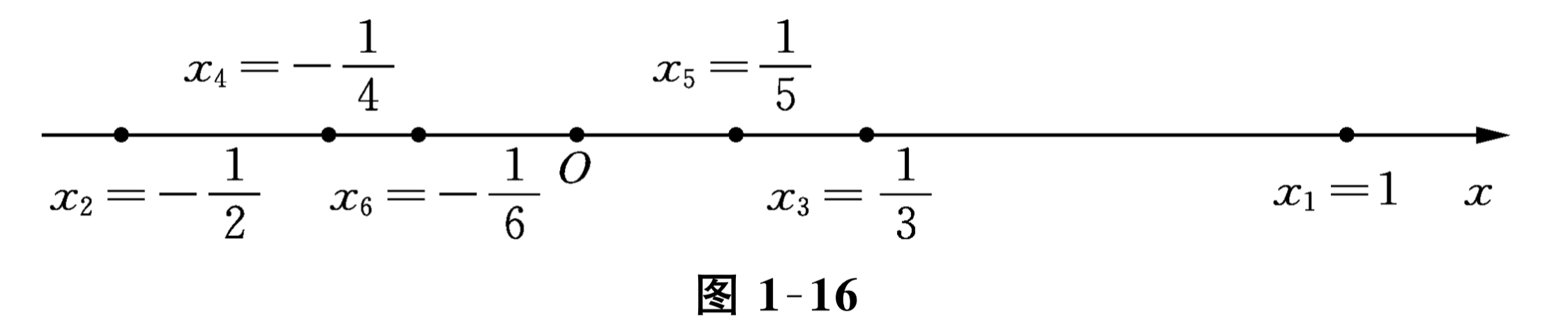
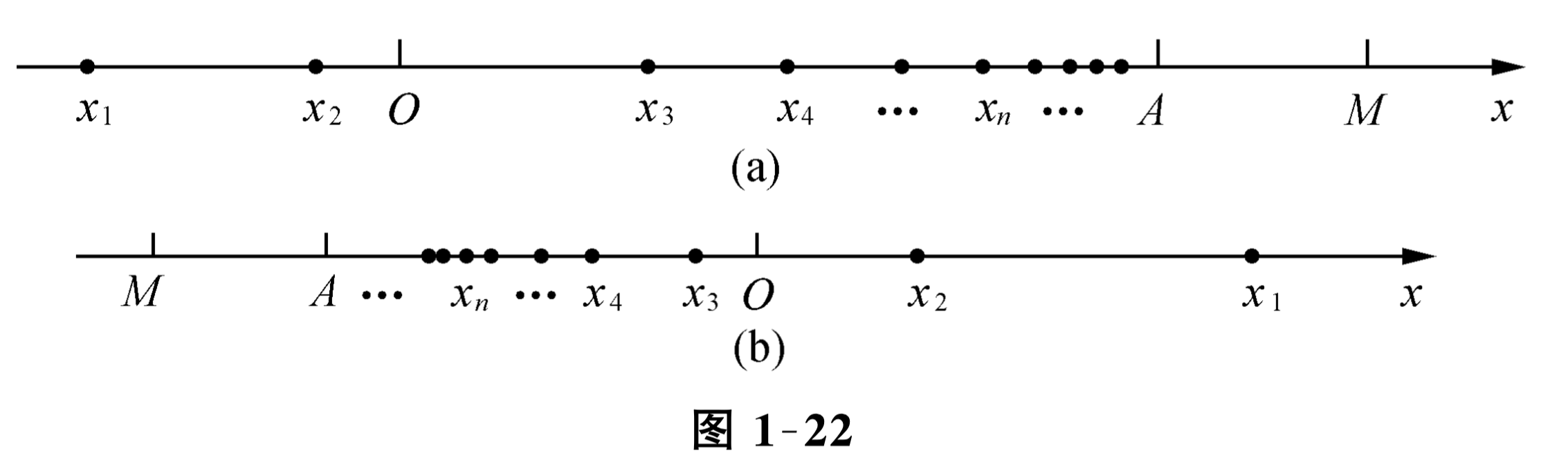
将一个数列的各项在数轴上用相应的点表示, 就可以得到这个数列的一幅简明图形, 如 \(\left\{(-1)^{n+1} \frac{1}{n}\right\}\) 的图形如图 1-16 所示. 因为数列是定义域为正整数集 \(\mathbf{N}_{+}\)的函数, 所以函数的有些特性, 如单调性、有界性等也可移用于数列.
  1. 单调性.
    若 \(x_{1} \leqslant x_{2} \leqslant x_{3} \leqslant \cdots \leqslant x_{n} \leqslant \cdots\text{,}\) 则称数列 \(\left\{x_{n}\right\}\) 为单调增加数列, 去等号后为严格单调增加数列. 若 \(x_{1} \geqslant x_{2} \geqslant x_{3} \geqslant \cdots \geqslant x_{n} \geqslant \cdots\text{,}\)则称数列 \(\left\{x_{n}\right\}\) 为单调减少数列, 去等号后为严格单调减少数列. 单调增加数列和单调减少数列统称为单调数列. 将单调数列 \(\left\{x_{n}\right\}\) 在数轴上用点表示, 那么这些点随着 \(n\) 的增大朝一个方向移动: 单调增加时, 朝 \(x\) 轴正向移动; 单调减少时,朝 \(x\) 轴负向移动.
  2. 有界性. 若存在一个正数 \(M\text{,}\) 对于任何正整数 \(n\text{,}\) 恒有 \(\left|x_{n}\right| \leqslant M\text{,}\) 则称数列 \(\left\{x_{n}\right\}\) 有界, 否则称 \(\left\{x_{n}\right\}\) 无界. 由 \(\left|x_{n}\right| \leqslant M\text{,}\) 得 \(-M \leqslant x_{n} \leqslant M\text{,}\) 所以从数轴上来看, 有界数列的点都落在有限区间 \([-M, M]\) 内. 反之,如果一个数列的一切点都落在区间 \([a, b]\) 内, 那么该数列是有界的.
在数列 \(\left\{x_{n}\right\}\) 中, 保持原有顺序, 依次取出无穷多项构成的新数列称为数列 \(\left\{x_{n}\right\}\) 的子数列, 简称子列. 如
\begin{equation*} \begin{aligned} \amp x_1, x_3, x_5, \cdots, x_{2 n-1}, \cdots ; \\ \amp x_1, x_3, x_7, \cdots, x_{2^n-1}, \cdots\end{aligned} \end{equation*}
都是 \(\left\{x_{n}\right\}\) 的子列, 一般子列记作
\begin{equation*} \left\{x_{n_{k}}\right\}: x_{n_{1}}, x_{n_{2}}, \cdots, x_{n_{k}}, \cdots . \end{equation*}

Subsubsection 1.2.1.2 数列的极限

一个变量在它的变化过程中无限接近某一个常量,这种现象称为极限现象.
Example 1.2.1.
例 1 我国古代哲学家庄子曾说: “一尺之棰, 日取其半,万世不竭.”(《天下篇》) 它描述了截取过程中棒长剩余量的变化,若用 \(x_{1}, x_{2}, x_{3}, \cdots\) 分别表示每次截取后剩余的棒长,则有
\begin{equation*} x_{n}=\frac{1}{2^{n}}, n=1,2,3, \cdots \end{equation*}
当 \(n\) 无限增大 (记为 \(n \rightarrow \infty\text{,}\) 读作 \(n\) 趋于无穷大), 棒长 \(x_{n}=\frac{1}{2^{n}}\) 无限接近于零.
Example 1.2.2.
例 2 我国古代数学家刘徽,通过计算圆的内接正多边形的面积来推算圆的面积一一割圆术,这是极限思想在几何上的应用. 它的计算过程如下： 在单位圆内分别作出内接正六边形、正十二边形, \(\cdots\text{,}\)正 \(3 \times 2^{n}\) 边形,面积依次为
\begin{equation*} A_{1}=3 \times 2^{0} \sin \frac{2 \pi}{3 \times 2}, A_{2}=3 \times 2 \sin \frac{2 \pi}{3 \times 2^{2}}, \cdots, A_{n}=3 \times 2^{n-1} \sin \frac{2 \pi}{3 \times 2^{n}}, \cdots \end{equation*}
它们构成一列有次序的数.
由几何直观可知, 当 \(n\) 越大, 圆的内接正多边形与圆的差别就越小, 以 \(A_{n}\) 为圆面积的近似值也越精确. 也就是说, 圆内接正多边形的边数无限增加时, 圆内接正多边形无限接近于圆, \(A_{n}\) 也无限接近于某一确定的数值, 这个数值就是圆的面积 \(\pi\text{.}\)
在上面的例子中, 当 \(n\) 无限增大时, \(\left\{\frac{1}{2^{n}}\right\}\) 越来越接近于 \(0,\left\{3 \times 2^{n-1} \sin \frac{2 \pi}{3 \times 2^{n}}\right\}\) 越来越接近于 \(\pi\text{.}\) 如果数列 \(\left\{x_{n}\right\}\) 当 \(n\) 无限增大时越来越接近于一个常数, 这个常数就称为数列 \(\left\{x_{n}\right\}\) 的极限. 在解决实际问题中形成的这种极限方法, 已经成为高等数学中的一种基本方法. 但是, 上述定义是很不严格的. 例如 \(\left\{\frac{1}{2^{n}}\right\}\text{,}\) 当 \(n\) 无限增大时, 它越来越接近于 0 ,也可以说它越来越接近于 \(-1\text{,}\) 但 \(-1\)不是 \(\left\{\frac{1}{2^{n}}\right\}\) 的极限. 如何准确地刻画“无限增大”与“越来越接近”呢？先看下面的例子.
Example 1.2.3.
例 3 考察数列 \(\left\{x_{n}\right\}=\left\{\frac{2 n+(-1)^{n+1}}{n}\right\}\) 的变化趋势. 因为 \(x_{n}=\frac{2 n+(-1)^{n+1}}{n}\text{,}\) 则 \(x_{n}-2=\frac{(-1)^{n+1}}{n}\text{,}\) 所以 \(\left|x_{n}-2\right|=\left|(-1)^{n+1} \frac{1}{n}\right|=\frac{1}{n}\text{.}\)
当 \(n\) 越来越大时, \(\frac{1}{n}\) 越来越小. 从几何上看, 在数轴上点 \(x_{n}\) 与点 2 的距离越来越小, 从而 \(x_{n}\) 越来越接近于 2 . 点 \(x_{n}\) 与点 2 的距离越来越小或者说要多小就有多小,其条件是只要 \(n\) 充分大. 例如: 要使 \(\left|x_{n}-2\right|<0.1\text{,}\) 即 \(\frac{1}{n}<0.1\text{,}\) 只要 \(n>10\) 时, 就有 \(\left|x_{n}-2\right|<0.1\text{;}\) 要使 \(\left|x_{n}-2\right|<0.01\text{,}\) 即 \(\frac{1}{n}<0.01\text{,}\) 只要 \(n>100\) 时, 就有 \(\left|x_{n}-2\right|<0.01 ;\) 要使 \(\left|x_{n}-2\right|<10^{-8}\text{,}\) 即 \(\frac{1}{n}<10^{-8}\text{,}\) 只要 \(n>10^{8}\) 时, 就有 \(\left|x_{n}-2\right|<10^{-8}\text{.}\) 一般地, 任意给定 \(\varepsilon>0\) ( \(\varepsilon\) 表示非常小的正实数), 要使 \(\left|x_{n}-2\right|<\varepsilon\text{,}\) 即 \(\frac{1}{n}<\varepsilon\text{,}\)只要 \(n>\frac{1}{\varepsilon}\text{.}\) 于是, 取 \(N=\left[\frac{1}{\varepsilon}\right]\text{,}\) 则当 \(n>N\) 时, 就有 \(\left|x_{n}-2\right|<\varepsilon\text{.}\)
上述不等式精确地刻画了数列 \(\left\{x_{n}\right\}\) 随 \(n\) 无限增大而与常数 2 越来越接近的变化趋势. 由于 \(\varepsilon\) 的任意性 (不管它多么小), \(\left|x_{n}-2\right|<\varepsilon\) 刻画了数列 \(\left\{x_{n}\right\}\) 与常数 2 越来越接近这一概念; 而 \(n>N\) 时, 则刻画了 \(n\) 无限增大过程中数列 \(\left\{x_{n}\right\}\) 在 \(n>N\) 以后的取值情况.
Definition 1.2.4.
定义 1 设 \(\left\{x_{n}\right\}\) 为一数列, 若存在常数 \(a\text{,}\)对于任意给定的正数 \(\varepsilon\) (不论它多么小), 总存在正整数 \(N\text{,}\) 使得当 \(n>N\) 时, 有
\begin{equation*} \left|x_{n}-a\right|<\varepsilon, \end{equation*}
则称 \(a\) 为数列 \(\left\{x_{n}\right\}\) 的极限, 或称数列 \(\left\{x_{n}\right\}\) 收敛于 \(a\text{,}\) 记作
\begin{equation*} \lim\limits_{n \rightarrow \infty} x_{n}=a, \text{ 或 } x_{n} \rightarrow a(n \rightarrow \infty). \end{equation*}
如果不存在这样的常数 \(a\text{,}\) 就认为数列 \(\left\{x_{n}\right\}\) 没有极限, 或者认为数列 \(\left\{x_{n}\right\}\) 是发散的. 习惯上也认为 \(\lim\limits_{n \rightarrow \infty} x_{n}\) 不存在. 注意
  1. 上述定义中,正数 \(\varepsilon\) 用来刻画数列 \(\left\{x_{n}\right\}\) 与常数 \(a\) 接近的程度, \(\varepsilon>0\) 可以任意小, 当 \(n\) 无限增大时, \(x_{n}\) 与 \(a\) 之差的绝对值可以小于事先给定的任意小正数 \(\varepsilon\text{;}\) 正整数 \(N\) 与任意给定的正数 \(\varepsilon\) 有关 (但不唯一), 它随着正数 \(\varepsilon\) 的确定而确定.
  2. 从几何直观看, 若数列 \(\left\{x_{n}\right\}\) 收敛于 \(a\text{,}\) 则对于 \(a\) 点的任何一个邻域 ( \(a-\varepsilon\text{,}\) \(a+\varepsilon\) ), 都存在正整数 \(N\text{,}\) 使数列 \(\left\{x_{n}\right\}\) 第 \(N\) 项以后的点全部落人该邻域内 (见 图1-17).
  3. 数列 \(\left\{x_{n}\right\}\) 的极限 \(a\) 是一个常数, 它表示了变量 \(x_{n}\) 随 \(n\) 增大时的变化趋势.
Example 1.2.5.
例 4 设 \(\left\{x_{n}\right\}=\{C\}\) ( \(C\) 为常数), 证明 \(\lim\limits_{n \rightarrow \infty} x_{n}=C\text{.}\)
Solution.
证 因对任意给定的 \(\varepsilon>0\text{,}\) 对于一切自然数 \(n\text{,}\) 恒有 \(\left|x_{n}-C\right|=|C-C|=0<\varepsilon\text{,}\) 所以
\begin{equation*} \lim\limits_{n \rightarrow \infty} x_{n}=C \end{equation*}
即常数列的极限等于同一常数.
注意 用定义证明数列极限存在的关键是: 对任意给定的 \(\varepsilon>0\text{,}\) 寻找到一个 \(N\) (不必要求最小的 \(N\) ), 使得定义中的有关关系成立.
Example 1.2.6.
例 5 设 \(|q|<1\text{,}\) 用定义证明数列 \(\left\{x_{n}\right\}=\left\{q^{n-1}\right\}\) 收敛于 0 .
Solution.
证 任给 \(\varepsilon>0\) (设 \(\varepsilon<1\) ), 因为
\begin{equation*} \left|x_{n}-0\right|=\left|q^{n-1}-0\right|=|q|^{n-1}, \end{equation*}
要使
\begin{equation*} \left|x_{n}-0\right|<\varepsilon, \end{equation*}
只要
\begin{equation*} |q|^{n-1}<\varepsilon . \end{equation*}
两边取自然对数, 得 \((n-1) \ln |q|<\ln \varepsilon\text{.}\) 因为
\begin{equation*} |q|<1, \ln |q|<0, \end{equation*}
故
\begin{equation*} n>1+\frac{\ln \varepsilon}{\ln |q|} . \end{equation*}
取 \(N=\left[1+\frac{\ln \varepsilon}{\ln |q|}\right]\text{,}\) 则当 \(n>N\) 时,有
\begin{equation*} \left|q^{n-1}-0\right|<\varepsilon, \end{equation*}
即
\begin{equation*} \lim\limits_{n \rightarrow \infty} q^{n-1}=0 . \end{equation*}
Example 1.2.7.
例 6 用定义证明 \(\lim\limits_{n \rightarrow \infty} \frac{n^{2}-2}{n^{2}+n+1}=1\text{.}\)
Solution.
证 任给 \(\varepsilon>0\text{,}\) 由于 \(\left|\frac{n^{2}-2}{n^{2}+n+1}-1\right|=\frac{3+n}{n^{2}+n+1}<\frac{n+n}{n^{2}}=\frac{2}{n}(n>3)\text{,}\)要使 \(\left|\frac{n^{2}-2}{n^{2}+n+1}-1\right|<\varepsilon\text{,}\) 只要
\begin{equation*} \frac{2}{n}<\varepsilon \text {, 即 } n>\frac{2}{\varepsilon} \text {. } \end{equation*}
因此,对任给的 \(\varepsilon>0\text{,}\) 取 \(N=\max \left\{\left[\frac{2}{\varepsilon}\right], 3\right\}\text{,}\) 则当 \(n>N\) 时, 有
\begin{equation*} \left|\frac{n^{2}-2}{n^{2}+n+1}-1\right|<\varepsilon \end{equation*}
即
\begin{equation*} \lim\limits_{n \rightarrow \infty} \frac{n^{2}-2}{n^{2}+n+1}=1 \end{equation*}
Technology 1.2.8. 微课视频.
用定义证明: \(\lim\limits_{n \rightarrow \infty}\left(\frac{1}{3}-\frac{1}{2n}+\frac{1}{6n^2}\right)=\frac{1}{3}\)
Solution.
Figure 1.2.9. 视频讲解

Subsubsection 1.2.1.3 收敛数列的性质

Proof.
证 (反证法) 设 \(\lim\limits_{n \rightarrow \infty} x_{n}=a, \lim\limits_{n \rightarrow \infty} x_{n}=b\text{,}\) 且 \(a \neq b\text{,}\) 不妨设 \(a<b\text{,}\) 取 \(\varepsilon_{0}=\frac{b-a}{2}\text{.}\) 由于 \(\lim\limits_{n \rightarrow \infty} x_{n}=a\text{,}\) 对于 \(\varepsilon_{0}=\frac{b-a}{2}\text{,}\) 存在 \(N_{1}\text{,}\) 当 \(n>N_{1}\) 时,有
\begin{equation*} \begin{gathered} \left|x_{n}-a\right|<\varepsilon_{0}=\frac{b-a}{2}, \\ a-\frac{b-a}{2}<x_{n}<a+\frac{b-a}{2}=\frac{b+a}{2} ; \end{gathered} \end{equation*}
又由于 \(\lim\limits_{n \rightarrow \infty} x_{n}=b\text{,}\) 对于 \(\varepsilon_{0}=\frac{b-a}{2}\text{,}\) 存在 \(N_{2}\text{,}\) 当 \(n>N_{2}\) 时, 有
\begin{equation*} \begin{gathered} \left|x_{n}-b\right|<\varepsilon_{0}=\frac{b-a}{2}, \\ \frac{b+a}{2}=b-\frac{b-a}{2}<x_{n}<b+\frac{b-a}{2} . \end{gathered} \end{equation*}
取 \(N=\max \left\{N_{1}, N_{2}\right\}\text{,}\) 则当 \(n>N\) 时, 既有 \(x_{n}<\frac{b+a}{2}\text{,}\) 又有 \(x_{n}>\frac{b+a}{2}\text{,}\) 但这是不可能的. 故必有 \(a=b\text{.}\) 定理证毕.
Proof.
证 设 \(\lim\limits_{n \rightarrow \infty} x_{n}=a\text{,}\) 对 \(\varepsilon_{0}=1\text{,}\) 存在正整数 \(N\text{,}\) 当 \(n>N\) 时, \(\left|x_{n}-a\right|<\varepsilon_{0}=1\text{,}\)而
\begin{equation*} \left|x_{n}\right|=\left|x_{n}-a+a\right| \leqslant\left|x_{n}-a\right|+|a|<1+|a| \text {, } \end{equation*}
取 \(M=\max \left\{\left|x_{1}\right|,\left|x_{2}\right|, \cdots,\left|x_{N}\right|, 1+|a|\right\}\text{,}\) 则对于一切自然数 \(n\text{,}\) 都有
\begin{equation*} \left|x_{n}\right| \leqslant M \text {, } \end{equation*}
故收敛数列 \(\left\{x_{n}\right\}\) 有界. 定理证毕.
本定理说明: 有界性是数列收敛的必要条件, 但应当注意, 它不是充分条件.如 \(\left\{\sin \frac{n \pi}{2}\right\}\) 有界,但不收敛.
Proof.
证 不妨设 \(a>0\text{,}\) 由 \(\lim\limits_{n \rightarrow \infty} x_{n}=a\text{,}\) 按照定义对 \(\varepsilon_{0}=\frac{a}{2}>0\text{,}\) 存在正整数 \(N\text{,}\) 当 \(n>N\)时, 有
\begin{equation*} \begin{gathered} \left|x_{n}-a\right|<\varepsilon_{0}=\frac{a}{2}, \\ \text{ 即 }-\frac{a}{2}<x_{n}-a<\frac{a}{2}, \\ \text{ 则 }0<\frac{a}{2}<x_{n}<\frac{3 a}{2}, \end{gathered} \end{equation*}
因此,当 \(n>N\) 时, \(x_{n}\) 与 \(a\) 同号. 定理证毕.
根据子列与极限的定义,还可得到以下定理.
由此可见, 若数列的某一子列发散, 或者它的两个子列收敛于不同的极限, 则该数列必定发散. 例如, 数列 \(\left\{(-1)^{n+1}\right\}\) 的两个子列
\begin{equation*} 1,1,1, \cdots, 1, \cdots \text { 及 }-1,-1,-1, \cdots,-1, \cdots \end{equation*}
分别收敛于 \(1\) 和 \(-1\text{,}\) 故原级数发散.

Subsection 1.2.2 函数的极限及其性质

数列是定义在正整数集上的函数. 数列 \(\left\{x_{n}\right\}\) 的极限为 \(a\text{,}\) 就是当自变量 \(n\) 无限增大时, 函数 \(x_{n}=f(n)\) 无限接近常数 \(a\text{.}\) 数列的极限可以看作函数 \(x_{n}=f(n)\) 当自变量 \(n \rightarrow \infty\) 时的极限. 若僘开数列极限概念中自变量 \(n\) 和函数值 \(f(n)\) 的特殊性,由此可引出函数极限的一般概念: 在自变量 \(x\) 的某个变化过程中,若对应的函数值 \(f(x)\) 无限接近于某个确定的数 \(A\text{,}\)则 \(A\) 就称为 \(x\) 在该变化过程中函数 \(f(x)\) 的极限. 显然, 函数的极限是与自变量的变化过程密切相关的. 由于自变量的变化过程不同, 函数的极限就表现为不同的形式.

Subsubsection 1.2.2.1 自变量趋于无穷大时函数的极限

设函数 \(f(x)\) 在自变量 \(x\) 的绝对值 \(|x|\) 无限增大时均有定义,下面给出当 \(x \rightarrow \infty\) 时, \(f(x)\) 的极限定义.
Definition 1.2.15.
定义 2 设 \(A\) 是一个常数, 若对于任意给定的正数 \(\varepsilon\) (不论它多么小), 总存在 \(X>0\text{,}\)使得当 \(|x|>X\) 时,恒有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称 \(A\) 是函数 \(f(x)\) 当 \(x \rightarrow \infty\) 时的极限, 记作
\begin{equation*} \lim\limits_{x \rightarrow \infty} f(x)=A \text { 或 } f(x) \rightarrow A \text { (当 } x \rightarrow \infty \text { ). } \end{equation*}
将这一定义与数列极限定义比较, 可以看出: 极限是一个常量, 它是用来描写 一个变量的变化趋势, 在自变量的某一变化趋势下, 函数与该常数之差的绝对值可任意地小. 与数列极限中 \(n\) 取自然数, 并无限增大的过程稍有不同, \(x \rightarrow \infty\) 是指其绝对值无限增大的过程,而 \(n \rightarrow \infty\) 是 \(x \rightarrow \infty\) 的一个特殊情形. \(x \rightarrow \infty\) 可以包含 \(x \rightarrow+\infty\) 与 \(x \rightarrow-\infty\) 两种情况.
Definition 1.2.16.
定义 3 设函数 \(f(x)\) 在 \((a,+\infty)\) 内有定义 ( \(a\) 为常数), 若任给 \(\varepsilon>0\text{,}\) 存在 \(X>0\text{,}\)使得当 \(x>X\) 时,恒有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称常数 \(A\) 为函数 \(f(x)\) 当 \(x \rightarrow+\infty\) 时的极限, 记作
\begin{equation*} \lim\limits_{x \rightarrow+\infty} f(x)=A \text { 或 } f(x) \rightarrow A(\text { 当 } x \rightarrow+\infty) \text {. } \end{equation*}
Definition 1.2.17.
定义 4 设函数 \(f(x)\) 在 \((-\infty, b)\) 内有定义 ( \(b\) 为常数), 若任给 \(\varepsilon>0\text{,}\) 存在 \(X>0\text{,}\) 使得当 \(x<-X\) 时, 恒有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称常数 \(A\) 为函数 \(f(x)\) 当 \(x \rightarrow-\infty\) 时的极限, 记作
\begin{equation*} \lim\limits_{x \rightarrow-\infty} f(x)=A \text { 或 } f(x) \rightarrow A(\text { 当 } x \rightarrow-\infty) \text {. } \end{equation*}
函数极限的定义 Definition 1.2.15 \(\sim \) Definition 1.2.17的几何意义分别如图 1-18a\(\sim \) c 所示.
Proof.
证 必要性. 因为 \(\lim\limits_{x \rightarrow \infty} f(x)=A\text{,}\) 由Definition 1.2.15 对任给 \(\varepsilon>0\text{,}\) 存在 \(X>0\text{,}\) 当 \(|x|>X\)时, 有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
所以,当 \(x>X\) 和 \(x<-X\) 时,都有
\begin{equation*} |f(x)-A|<\varepsilon . \end{equation*}
由Definition 1.2.16和 Definition 1.2.17可得 \(\quad \lim\limits_{x \rightarrow+\infty} f(x)=\lim\limits_{x \rightarrow-\infty} f(x)=A\text{.}\) 充分性. 因为 \(\lim\limits_{x \rightarrow+\infty} f(x)=A\text{,}\) 由Definition 1.2.16 知, 对任给 \(\varepsilon>0\text{,}\) 存在 \(X_{1}>0\text{,}\) 当 \(x>X_{1}\) 时, 有
\begin{equation*} |f(x)-A|<\varepsilon . \end{equation*}
又因为 \(\lim f(x)=A\text{,}\) 由Definition 1.2.17 知, 对上述 \(\varepsilon>0\text{,}\) 存在 \(X_{2}>0\text{,}\) 当 \(x<-X_{2}\)时, 有
\begin{equation*} |f(x)-A|<\varepsilon . \end{equation*}
取 \(X=\max \left\{X_{1}, X_{2}\right\}\text{,}\) 则当 \(|x|>X\) 时,恒有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
故由Definition 1.2.15pretext view web 可得 \(\lim\limits_{x \rightarrow \infty} f(x)=A\text{.}\) 定理证毕.
Example 1.2.19.
例 7 证明 \(\lim\limits_{x \rightarrow \infty} \frac{1-x}{x+1}=-1\text{.}\)
Solution.
任给 \(\varepsilon>0\text{,}\) 要证明存在正数 \(X\text{,}\) 当 \(|x|>X\) 时, 恒有 \(\left|\frac{1-x}{x+1}-(-1)\right|<\varepsilon\text{.}\)
于是, 由 \(\left|\frac{1-x}{x+1}-(-1)\right|=\left|\frac{2}{x+1}\right| \leqslant \frac{2}{|x|-1}<\varepsilon(\) 限制 \(|x|>1) ，\) 得
\begin{equation*} |x|>\frac{2}{\varepsilon}+1,|x|>1 . \end{equation*}
因此, 若取 \(X=\frac{2}{\varepsilon}+1\text{,}\) 则当 \(|x|>X\) 时, 就有 \(\left|\frac{1-x}{x+1}-(-1)\right|<\varepsilon\text{,}\) 即
\begin{equation*} \lim\limits_{x \rightarrow \infty} \frac{1-x}{x+1}=-1 \end{equation*}

Subsubsection 1.2.2.2 自变量趋于有限值时函数的极限

讨论当自变量 \(x\) 趋于有限值 \(x_{0}\) 时, \(f(x)\) 无限接近于一个常数 \(A\) 的情形. 它与前面讨论过的情形相比,其差异仅在于 \(x\) 的趋向不同而已. 显然, \(f(x)\) 无限接近于常数 \(A\text{,}\) 其含义与前面一样, 可以用 \(|f(x)-A|<\varepsilon\) 来描述. 但 \(|f(x)-A|<\varepsilon\) 并非对任何 \(x\) 都要成立, 它只要求在 \(x\) 趋于 \(x_{0}\text{,}\) 即 \(x\) 充分接近 \(x_{0}\) 时成立. \(x\) 充分接近 \(x_{0}\) 可以用 \(x_{0}\) 的一个充分小的 \(\delta\) 邻域来描述.
Example 1.2.20.
例 8 考察函数 \(f(x)=\frac{x^{2}-4}{3(x-2)}\) 当 \(x \rightarrow 2\) 时的变化趋势.
Solution.
解: 易见当 \(x \rightarrow 2\) 时, \(f(x)\) 与 \(\frac{4}{3}\) 无限接近 (见图 1-19).
当 \(x \neq 2\) 时, \(\left|f(x)-\frac{4}{3}\right|=\left|\frac{x^{2}-4}{3(x-2)}-\frac{4}{3}\right|=\frac{1}{3}|x-2|\text{.}\)
要使 \(\left|f(x)-\frac{4}{3}\right|<0.01\text{,}\) 只要 \(0<|x-2|<0.03\text{;}\) 要使 \(\left|f(x)-\frac{4}{3}\right|<0.001\text{,}\) 只要 \(0<|x-2|<0.003 ;\) 要使 \(\left|f(x)-\frac{4}{3}\right|<\varepsilon\text{,}\) 只要 \(0<|x-2|<3 \varepsilon=\delta(\varepsilon)\text{.}\)
Definition 1.2.21.
定义 5 设函数 \(f(x)\) 在 \(x_{0}\) 的某去心邻域内有定义, \(A\) 为常数,若对任意给定的 \(\varepsilon>0\text{,}\) 存在 \(\delta>0\text{,}\) 使得当 \(0<\left|x-x_{0}\right|<\delta\) 时, 恒有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称常数 \(A\) 为函数 \(f(x)\) 当 \(x \rightarrow x_{0}\) 时的极限,记作
\begin{equation*} \lim\limits_{x \rightarrow x_{0}} f(x)=A \text { 或 } f(x) \rightarrow A\left(\text { 当 } x \rightarrow x_{0}\right) \text {. } \end{equation*}
从几何图形上看 (见图 1-20), 对于任给的 \(\varepsilon>0\text{,}\)总能求得一个 \(\delta>0\text{,}\) 使得在 \(x_{0}\) 的 \(\delta\) 去心邻域 \(\stackrel{\circ}{U}\left(x_{0}\right.\text{,}\) \(\delta)\) 内, \(y=f(x)\) 的图形落在两条平行直线 \(y=A+\varepsilon\text{,}\) \(y=A-\varepsilon\) 之间.
由Definition 1.2.21 , 容易证明
\begin{equation*} \lim\limits_{x \rightarrow x_{0}} C=C, \lim\limits_{x \rightarrow x_{0}} x=x_{0} \end{equation*}
Example 1.2.22.
例 9 证明 \(\lim\limits_{x \rightarrow 2}(2 x-3)=1\text{.}\)
Solution.
证 对任意给定的 \(\varepsilon>0\text{,}\)要使
\begin{equation*} |(2 x-3)-1|=2|x-2|<\varepsilon, \end{equation*}
只要
\begin{equation*} |x-2|<\frac{\varepsilon}{2} \text {. } \end{equation*}
于是, 取 \(\delta=\frac{\varepsilon}{2}\text{,}\) 则当 \(0<|x-2|<\delta\) 时, 有
\begin{equation*} |(2 x-3)-1|<\varepsilon, \end{equation*}
故
\begin{equation*} \lim\limits_{x \rightarrow 2}(2 x-3)=1 . \end{equation*}
Example 1.2.23.
例 10 证明: 当 \(x_{0}>0\) 时, \(\lim\limits_{x \rightarrow x_{0}} \sqrt{x}=\sqrt{x_{0}}\text{.}\)
Solution.
任给 \(\varepsilon>0\text{,}\) 要使 \(|f(x)-A|=\left|\sqrt{x}-\sqrt{x_{0}}\right|=\left|\frac{x-x_{0}}{\sqrt{x}+\sqrt{x_{0}}}\right| \leqslant \frac{\left|x-x_{0}\right|}{\sqrt{x_{0}}}<\varepsilon\text{,}\)只要 \(\left|x-x_{0}\right|<\sqrt{x_{0}} \varepsilon\) 且 \(x \geqslant 0\text{.}\) 于是, 只要取 \(\delta=\min \left\{x_{0}, \sqrt{x_{0}} \varepsilon\right\}\text{,}\) 则当 \(0<\left|x-x_{0}\right|<\delta\) 时, 就有 \(\left|\sqrt{x}-\sqrt{x_{0}}\right|<\varepsilon\text{,}\)所以
\begin{equation*} \lim\limits_{x \rightarrow x_{0}} \sqrt{x}=\sqrt{x_{0}} \end{equation*}
Example 1.2.24.
例 11 证明 \(\lim\limits_{x \rightarrow 0} \cos x=1\text{.}\)
Solution.
证 因为 \(x \rightarrow 0\text{,}\) 不妨设 \(|x|<\frac{\pi}{2}\text{,}\) 作单位圆 (见图1-21). 当 \(0<x<\frac{\pi}{2}\) 时, \(|\cos x-1|=\overline{O A}-\overline{O B}=\overline{B A}<\overline{A C}<\overparen{A C}=x\text{.}\)
由于 \(\cos (-x)=\cos x\text{,}\) 故当 \(0<|x|<\frac{\pi}{2}\) 时, 有
\begin{equation*} |\cos x-1|<|x| \end{equation*}
因此,对任给 \(\varepsilon>0\text{,}\) 要使 \(|\cos x-1|<|x|<\varepsilon\text{.}\) 只要取 \(\delta=\varepsilon\text{,}\) 当 \(0<|x|<\delta\) 时, 有 \(|\cos x-1|<\varepsilon\text{.}\) 所以
\begin{equation*} \lim\limits_{x \rightarrow 0} \cos x=1 . \end{equation*}
上面给出了当 \(x \rightarrow x_{0}\) 时 \(f(x)\) 的极限的定义,其中 \(x\) 既从 \(x_{0}\) 左侧也从 \(x_{0}\) 右侧趋向于 \(x_{0}\text{.}\) 但有时需要考虑 \(x\) 只从 \(x_{0}\) 的一侧趋于 \(x_{0}\) 的情形,这就需要引进下面单侧极限的概念.
Definition 1.2.25.
定义 6 若存在常数 \(A\text{,}\) 对任意给定的 \(\varepsilon>0\text{,}\) 存在 \(\delta>0\text{,}\) 当 \(x_{0}-\delta<x<x_{0}\)时, 有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称 \(A\) 为 \(f(x)\) 在 \(x_{0}\) 处的左极限, 记作 \(\lim\limits_{x \rightarrow x_{0}^{-}} f(x)=A\) 或 \(f\left(x_{0}-0\right)=A\text{.}\)
Definition 1.2.26.
定义 7 若存在常数 \(A\text{,}\)对任意给定的 \(\varepsilon>0\text{,}\) 存在 \(\delta>0\text{,}\) 当 \(x_{0}<x<x_{0}+\delta\)时, 有
\begin{equation*} |f(x)-A|<\varepsilon, \end{equation*}
则称 \(A\) 为 \(f(x)\) 在 \(x_{0}\) 处的右极限, 记作 \(\lim\limits_{x \rightarrow x_{0}^{+}} f(x)=A\) 或 \(f\left(x_{0}+0\right)=A\text{.}\)
关于函数的极限与左、右极限, 有下面的定理.
也就是说, 极限存在等价于左、右极限存在并且相等.
Example 1.2.28.
例 12 验证 \(\lim\limits_{x \rightarrow 0} \frac{|x|}{x}\) 不存在.
Solution.
证 \(\lim\limits_{x \rightarrow 0^{-}} \frac{|x|}{x}=\lim\limits_{x \rightarrow 0^{-}} \frac{-x}{x}=\lim\limits_{x \rightarrow 0^{-}}(-1)=-1\text{,}\)
\begin{equation*} \lim\limits_{x \rightarrow 0^{+}} \frac{|x|}{x}=\lim\limits_{x \rightarrow 0^{+}} \frac{x}{x}=\lim\limits_{x \rightarrow 0^{+}} 1=1 \end{equation*}
所以由Theorem 1.2.27 知, \(\lim\limits_{x \rightarrow 0} f(x)\) 不存在.

Subsubsection 1.2.2.3 函数极限的性质

对于函数的极限, 无论是 \(x \rightarrow x_{0}\) 或 \(x \rightarrow \infty\) 时, 都有类似于数列极限的一些性质. 对 \(x \rightarrow x_{0}\) 的情形叙述如下.
Proof.
证 设 \(\lim\limits_{x \rightarrow x_{0}} f(x)=A\text{,}\) 由定义知, 对 \(\varepsilon_{0}=1\text{,}\) 存在 \(\delta>0\text{,}\) 当 \(0<\left|x-x_{0}\right|<\delta\) 时, \(|f(x)-A|<\varepsilon_{0}=1\text{.}\) 因为
\begin{equation*} |f(x)| \leqslant|A|+|f(x)-A|<|A|+1, \end{equation*}
所以, 取 \(M=|A|+1\text{,}\) 则当 \(x \in \dot{U}\left(x_{0}, \delta\right),|f(x)| \leqslant M\text{,}\) 即 \(f(x)\) 在 \(\dot{U}\left(x_{0}, \delta\right)\) 内有界.
Proof.
证 不妨设 \(A>0\) ( \(A<0\) 的情形同理可证). 由定义知, 对于 \(\varepsilon_{0}=\frac{A}{2}\text{,}\) 存在 \(\delta>0\text{,}\) 当 \(0<\left|x-x_{0}\right|<\delta\) 时, \(|f(x)-A|<\varepsilon=\frac{A}{2}\text{,}\)即 \(A-\frac{A}{2}<f(x)<A+\frac{A}{2}\text{.}\) 所以, 当 \(x \in \dot{U}\left(x_{0}, \delta\right)\) 时, \(f(x)>\frac{A}{2}>0\text{.}\)
上述Corollary 1.2.32与Corollary 1.2.33 的证明留给读者. 对于 \(x \rightarrow x_{0}^{-}, x \rightarrow x_{0}^{+}\)以及 \(x \rightarrow \infty, x \rightarrow-\infty, x \rightarrow+\infty\) 的情形, 有类似于Theorem 1.2.29 \(\sim \) Theorem 1.2.31 的结论,这里不再详述.

Subsection 1.2.3 极限运算法则

Subsubsection 1.2.3.1 极限的四则运算

对于数列的极限, 有以下定理.
Proof.
证 这里只证 (2), 将 (1) 与 (3) 的证明留给读者. 对于任给的 \(\varepsilon>0\text{,}\) 要使 \(\left|x_{n} y_{n}-a b\right|<\varepsilon\text{,}\) 只要
\begin{equation*} \left|x_{n} y_{n}-a b\right|=\left|\left(x_{n} y_{n}-a y_{n}\right)+\left(a y_{n}-a b\right)\right| \leqslant\left|x_{n}-a\right|\left|y_{n}\right|+|a|\left|y_{n}-b\right|<\varepsilon . \end{equation*}
由于 \(y_{n}\) 收敛,故 \(\left\{y_{n}\right\}\) 有界, 即存在 \(M>0\text{,}\)使
\begin{equation*} \left|y_{n}\right| \leqslant M \quad(n=1,2, \cdots) . \end{equation*}
又因为 \(\lim x_{n}=a, \lim y_{n}=b\text{,}\) 所以对于上述任给的 \(\varepsilon>0\text{,}\) 存在正整数 \(N_{1}, N_{2}\text{,}\)当 \(n>N_{1}\) 时,有 \(\left|x_{n}-a\right|<\frac{\varepsilon}{2 M}\text{;}\) 当 \(n>N_{2}\) 时, 有 \(\left|y_{n}-b\right|<\frac{\varepsilon}{2|a|+1}\text{.}\) 取 \(N=\max \left\{N_{1}, N_{2}\right\}\text{,}\) 则当 \(n>N\) 时,不等式
\begin{equation*} \left|x_{n}-a\right|<\frac{\varepsilon}{2 M},\left|y_{n}-b\right|<\frac{\varepsilon}{2|a|+1} \end{equation*}
同时成立, 从而
\begin{equation*} \left|x_{n} y_{n}-a b\right| \leqslant\left|x_{n}-a\right|\left|y_{n}\right|+|a|\left|y_{n}-b\right|<\frac{\varepsilon}{2 M} M+|a| \frac{\varepsilon}{2|a|+1}<\varepsilon . \end{equation*}
因此, \(\lim\limits_{n \rightarrow \infty}\left(x_{n} y_{n}\right)=a \cdot b\text{.}\)
上述定理中 (1) 和 (2) 都可推广到有限个收敛数列的情形. 由 (2) 很容易得到:
Example 1.2.37.
例 13 求极限 \(\lim\limits_{n \rightarrow \infty} \frac{5 n^{2}+3}{3 n^{2}+7 n+12}\text{.}\)
Solution.
解 由于其中的分子与分母极限都不存在,故不能直接用Theorem 1.2.34 ,但变形后
\begin{equation*} x_{n}=\frac{5+\frac{3}{n^{2}}}{3+\frac{7}{n}+\frac{12}{n^{2}}} \end{equation*}
则由Theorem 1.2.34 及其Corollary 1.2.35 有
\begin{equation*} \lim\limits_{n \rightarrow \infty} x_{n}=\frac{\lim\limits_{n \rightarrow \infty} 5+3 \lim\limits_{n \rightarrow \infty} \frac{1}{n^{2}}}{\lim\limits_{n \rightarrow \infty} 3+7 \lim\limits_{n \rightarrow \infty} \frac{1}{n}+12 \lim\limits_{n \rightarrow \infty} \frac{1}{n^{2}}}=\frac{5}{3} . \end{equation*}
对于函数的极限, 也有类似的性质.
同样有
注意 Theorem 1.2.38及其推论对单侧极限也成立.
Example 1.2.41.
例 14 求 \(\lim\limits_{x \rightarrow-2} \frac{x^{2}+2 x}{3 x^{2}+x-10}\text{.}\)
Solution.
解 当 \(x \rightarrow-2\) 时, 分子、分母都趋于 0 ,不能直接利用Theorem 1.2.38 的结论. 但
\begin{equation*} \frac{x^{2}+2 x}{3 x^{2}+x-10}=\frac{x(x+2)}{(3 x-5)(x+2)}, \end{equation*}
由于 \(x \rightarrow-2\text{,}\) 但 \(x \neq-2\text{,}\) 所以 \(x+2 \neq 0\text{,}\) 可约去公因式 \(x+2\text{,}\) 再利用Theorem 1.2.38, 有
\begin{equation*} \lim\limits_{x \rightarrow-2} \frac{x^{2}+2 x}{3 x^{2}+x-10}=\lim\limits_{x \rightarrow-2} \frac{x}{3 x-5}=\frac{2}{11} . \end{equation*}
Example 1.2.42.
例 15 求 \(\lim\limits_{x \rightarrow 1} \frac{(1-\sqrt{x})(1-\sqrt[3]{x})(1-\sqrt[4]{x})}{(1-x)^{3}}\text{.}\)
Solution.
解 当 \(x \rightarrow 1\) 时, 分子、分母都趋于 0 ,不能直接利用Theorem 1.2.38pretext view web 的结论,而要先对函数作必要的变形. 由于分子中含有根式, 通常先进行根式有理化, 然后约去分 子、分母中的公因子.
\begin{equation*} \begin{aligned} & \lim\limits_{x \rightarrow 1} \frac{(1-\sqrt{x})(1-\sqrt[3]{x})(1-\sqrt[4]{x})}{(1-x)^{3}} \\ = & \lim\limits_{x \rightarrow 1} \frac{(1-x)(1-x)(1-x)}{(1-x)^{3}(1+\sqrt{x})\left(1+\sqrt[3]{x}+\sqrt[3]{x^{2}}\right)\left(1+\sqrt[4]{x}+\sqrt[4]{x^{2}}+\sqrt[4]{x^{3}}\right)} \\ = & \lim\limits_{x \rightarrow 1} \frac{1}{(1+\sqrt{x})\left(1+\sqrt[3]{x}+\sqrt[3]{x^{2}}\right)\left(1+\sqrt[4]{x}+\sqrt[4]{x^{2}}+\sqrt[4]{x^{3}}\right)}=\frac{1}{24} . \end{aligned} \end{equation*}
Example 1.2.43.
例 16 求下列极限: (1) \(\lim\limits_{x \rightarrow \infty} \frac{1000 x+2}{x^{2}+1}\text{;}\) (2) \(\lim\limits_{x \rightarrow \infty} \frac{2 x^{3}+3 x^{2}+5}{7 x^{3}+4 x^{2}-1}\text{.}\)
Solution.
解
  1. \(x \rightarrow \infty\) 时, 分子和分母的极限都不存在. 先用 \(x^{2}\) 去除分子分母,再求极限。
    \begin{equation*} \lim\limits_{x \rightarrow \infty} \frac{1000 x+2}{x^{2}+1}=\lim\limits_{x \rightarrow \infty} \frac{\frac{1000}{x}+\frac{2}{x^{2}}}{1+\frac{1}{x^{2}}}=\frac{1000 \lim\limits_{x \rightarrow \infty} \frac{1}{x}+2\left(\lim\limits_{x \rightarrow \infty} \frac{1}{x}\right)^{2}}{1+\left(\lim\limits_{x \rightarrow \infty} \frac{1}{x}\right)^{2}}=\frac{0}{1}=0 . \end{equation*}
  2. \(x \rightarrow \infty\) 时, 分子和分母的极限都不存在. 先用 \(x^{3}\) 去除分子分母, 再求极限.
    \begin{equation*} \lim\limits_{x \rightarrow \infty} \frac{2 x^{3}+3 x^{2}+5}{7 x^{3}+4 x^{2}-1}=\lim\limits_{x \rightarrow \infty} \frac{2+\frac{3}{x}+\frac{5}{x^{3}}}{7+\frac{4}{x}-\frac{1}{x^{3}}}=\frac{2}{7} . \end{equation*}

Subsubsection 1.2.3.2 复合函数的极限

在极限计算中,经常碰到复合函数极限的计算问题.
Proof.
证 要证对任给的 \(\varepsilon>0\text{,}\) 存在 \(\delta>0\text{,}\) 使当 \(0<\left|x-x_{0}\right|<\delta\) 时,有
\begin{equation*} |f[\varphi(x)]-A|<\varepsilon . \end{equation*}
对上述 \(\varepsilon>0\text{,}\) 存在 \(\eta>0\text{,}\) 使当 \(0<\left|u-u_{0}\right|<\eta\) 时,有
\begin{equation*} |f(u)-A|<\varepsilon . \end{equation*}
由 \(\lim\limits_{x \rightarrow x_{0}} \varphi(x)=u_{0}\) 知, 对于 \(\eta>0\text{,}\) 存在 \(0<\delta<\delta_{0}\text{,}\) 当 \(0<\left|x-x_{0}\right|<\delta\) 时, 有
\begin{equation*} \left|\varphi(x)-u_{0}\right|<\eta . \end{equation*}
当 \(0<\left|x-x_{0}\right|<\delta\) 时, \(\left|\varphi(x)-u_{0}\right|<\eta\) 且 \(\left|\varphi(x)-u_{0}\right| \neq 0\text{,}\) 即有
\begin{equation*} 0<\left|\varphi(x)-u_{0}\right|<\eta \text {, 及 }|f[\varphi(x)]-A|=|f(u)-A|<\varepsilon \text {. } \end{equation*}
定理证毕.
Theorem 1.2.44表明,如果函数 \(f(u)\) 和 \(\varphi(x)\) 满足定理的条件,那么作代换 \(u=\varphi(x)\)可以把 \(\lim\limits_{x \rightarrow x_{0}} f[\varphi(x)]\) 化为求 \(\lim\limits_{u \rightarrow u_{0}} f(u)\text{,}\) 其中 \(u_{0}=\lim\limits_{x \rightarrow x_{0}} \varphi(x)\text{.}\)

Subsection 1.2.4 极限存在准则 两个重要极限

Subsubsection 1.2.4.1 极限存在准则

现在介绍判定极限存在的几个准则.
Proof.
证 由数列极限的定义,对于任给的 \(\varepsilon>0\text{,}\) 存在正整数 \(N_{1}\text{,}\) 当 \(n>N_{1}\) 时, 有 \(\left|y_{n}-a\right|<\varepsilon\text{;}\) 又存在正整数 \(N_{2}\text{,}\) 当 \(n>N_{2}\) 时, 有 \(\left|z_{n}-a\right|<\varepsilon\text{.}\) 现取 \(N=\max \left\{N_{1}, N_{2}\right\}\text{,}\) 则当 \(n>N\) 时, 上述两式同时成立, 即有
\begin{equation*} a-\varepsilon<y_{n}<a+\varepsilon, a-\varepsilon<z_{n}<a+\varepsilon, \end{equation*}
\begin{equation*} \text{又由 (1) 有}\hspace{0.5cm} a-\varepsilon<y_{n}<x_{n} <z_{n}<a+\varepsilon, \end{equation*}
\begin{equation*} \text{所以 }\hspace{1cm} |x_{n}-a|< \varepsilon \end{equation*}
\begin{equation*} \text{故}\hspace{1cm} \lim\limits_{n \rightarrow \infty} x_{n}=a. \end{equation*}
注意到 \(n \rightarrow \infty\text{,}\) 条件 (1) 只需从某个自然数起成立即可. 上述数列极限存在准则容易推广到函数极限的情形.
Example 1.2.47.
例 17 求下列数列的极限:
(1) \(\lim\limits_{n \rightarrow \infty} \frac{n !}{n^{n}}\text{;}\) (2) \(\lim\limits_{n \rightarrow \infty}\left(\frac{1}{\sqrt{n^{2}+1}}+\frac{1}{\sqrt{n^{2}+2}}+\cdots+\frac{1}{\sqrt{n^{2}+n}}\right)\text{.}\)
Solution.
解
  1. 因为 \(0<\frac{n !}{n^{n}}=\frac{1 \cdot 2 \cdot \cdots \cdot(n-1) \cdot n}{n \cdot n \cdot \cdots \cdot n \cdot n}<\frac{1}{n}\text{,}\) 又因为 \(\lim\limits_{n \rightarrow \infty} \frac{1}{n}=0\text{,}\) 所以由Proposition 1.2.45, 有 \(\lim\limits_{n \rightarrow \infty} \frac{n !}{n^{n}}=0\text{.}\)
  2. 因为
    \begin{equation*} \frac{n}{\sqrt{n^{2}+n}}<\frac{1}{\sqrt{n^{2}+1}}+\cdots+\frac{1}{\sqrt{n^{2}+n}}<\frac{n}{\sqrt{n^{2}+1}}, \end{equation*}
    又因为 \(\lim\limits_{n \rightarrow \infty} \frac{n}{\sqrt{n^{2}+n}}=\lim\limits_{n \rightarrow \infty} \frac{1}{\sqrt{1+\frac{1}{n}}}=1, \lim\limits_{n \rightarrow \infty} \frac{n}{\sqrt{n^{2}+1}}=\lim\limits_{n \rightarrow \infty} \frac{1}{\sqrt{1+\frac{1}{n^{2}}}}=1\text{,}\) 所以由Proposition 1.2.45 , 有 \(\lim\limits_{n \rightarrow \infty}\left(\frac{1}{\sqrt{n^{2}+1}}+\frac{1}{\sqrt{n^{2}+2}}+\cdots+\frac{1}{\sqrt{n^{2}+n}}\right)=1\text{.}\)
Proposition 1.2.48 的严格证明超出本书的要求,这里从略. 但从几何上看, 它的正确性是显然的. 因为数列 \(\left\{x_{n}\right\}\) 单调增加 (减少) 时, 它的各项所表示的点都朝 \(x\) 轴正 (负)方向移动, 这种移动只能有两个结果, 一是沿 \(x\) 轴正 (负) 向无限远移, 另一个是无限接近一个定点 \(A\text{,}\) 而又不超过 \(A\text{.}\) 由于 \(\left\{x_{n}\right\}\) 有界, 故前一情况是不可能的,而只能出现后一情况. 此时, \(A\) 就是 \(\left\{x_{n}\right\}\) 的极限 (见图 1-22).
Proposition 1.2.48 可叙述为, 单调增加有上界或单调减少有下界的数列必有极限.

Subsubsection 1.2.4.2 重要极限一 \(\lim\limits_{x \rightarrow 0} \frac{\sin x}{x}=1\)

事实上, 因为 \(x \rightarrow 0\text{,}\) 不妨设 \(0<x<\frac{\pi}{2}\text{,}\) 作单位圆 (见图 1-21), 显然有
\begin{equation*} \overline{B C}=\sin x, \overparen{A C}=x, \overline{A D}=\tan x \end{equation*}
\(\triangle A O C\) 的面积 \(<\) 扇形 \(A O C\) 的面积 \(<\triangle A O D\) 的面积.
所以
\begin{equation*} \frac{1}{2} \sin x<\frac{1}{2} x<\frac{1}{2} \tan x, \end{equation*}
即
\begin{equation*} \sin x<x<\tan x . \end{equation*}
上式除以 \(\sin x\text{,}\) 有
\begin{equation*} 1<\frac{x}{\sin x}<\frac{1}{\cos x} \end{equation*}
即
\begin{equation*} \cos x<\frac{\sin x}{x}<1 . \end{equation*}
又因为 \(f(x)=\frac{\sin x}{x}(x \neq 0)\) 为偶函数, 故当 \(0<|x|<\frac{\pi}{2}\) 时,
\begin{equation*} \cos x<\frac{\sin x}{x}<1 \end{equation*}
由Example 1.2.24 知, \(\lim\limits_{x \rightarrow 0} \cos x=1\text{.}\) 又 \(\lim\limits_{x \rightarrow 0} 1=1\text{,}\) 故由Proposition 1.2.46 , 有
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{\sin x}{x}=1 \end{equation*}
Example 1.2.49.
例 18 求 \(\lim\limits_{x \rightarrow 0} \frac{\tan x}{x}\text{.}\)
Solution.
解 \(\lim\limits_{x \rightarrow 0} \frac{\tan x}{x}=\lim\limits_{x \rightarrow 0} \frac{\sin x}{x} \cdot \frac{1}{\cos x}=1\text{.}\)
Example 1.2.50.
例 19 求 \(\lim\limits_{x \rightarrow 0} \frac{x}{\arcsin x}\text{.}\)
Solution.
解 令 \(u=\arcsin x\text{,}\) 则 \(x=\sin u\text{,}\) 当 \(x \rightarrow 0\) 时, \(u \rightarrow 0\text{.}\) 所以
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{x}{\arcsin x}=\lim\limits_{u \rightarrow 0} \frac{\sin u}{u}=1 . \end{equation*}
上述变量代换的方法也可以不明显写出来.
Example 1.2.51.
例 20 求 \(\lim\limits_{x \rightarrow 0} \frac{1-\cos x}{x^{2}}\text{.}\)
Solution.
解 \(\lim\limits_{x \rightarrow 0} \frac{1-\cos x}{x^{2}}=\lim\limits_{x \rightarrow 0} \frac{2 \sin ^{2} \frac{x}{2}}{x^{2}}=\lim\limits_{x \rightarrow 0} \frac{2 \sin ^{2} \frac{x}{2}}{2^{2}\left(\frac{x}{2}\right)^{2}}=\frac{1}{2} \lim\limits_{x \rightarrow 0}\left(\frac{\sin \frac{x}{2}}{\frac{x}{2}}\right)^{2}=\frac{1}{2}\text{.}\)
Project 1.2.1. 发现之旅: 存款的艺术.
为方便起见，我们假设你有1元钱想存银行，银行年利率是100%。银行为招揽顾客，给出如下优惠政策: 你可以存1年内的任意时间。
问题:选择最优策略，使得1年后的收益最高.
(a)
请列出分别按照一年，半年，一个季度和半个季度的策略存款的最终收益。
Hint.
该题锻炼你系统处理问题的能力！
Exercises 练习题:多选题
1.
    下列哪个说法是正确的.
  • 存款重复次数越多, 收益越高
  • 利息生利息. 半年期存款的策略的多余收益来源于前半年的利息.
  • 数列\(\{(1+1/n)^n\}\)是单调增的
  • 证明参见下个练习题.
  • 如果存款次数趋于无穷大, 你将成为百万富翁.
  • 数列不一定是无界的.
(b)
用软件发现数列\(\{(1+1/n)^n\}\)的单调性和有界性.
Figure 1.2.52. 数列\(\{(1+1/n)^n\}\)的性质
Example 1.2.53.
例 21 证明 \(\lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}=\mathrm{e}\text{.}\)
Solution.
证 设 \(x_{n}=\left(1+\frac{1}{n}\right)^{n}\text{,}\) 可以证明数列 \(\left\{x_{n}\right\}\) 单调增加且有上界. 因为
\begin{equation} \begin{aligned} x_{n}= & \left(1+\frac{1}{n}\right)^{n}=1+\mathrm{C}_{n}^{1} \frac{1}{n}+\mathrm{C}_{n}^{2} \frac{1}{n^{2}}+\cdots+\mathrm{C}_{n}^{n} \frac{1}{n^{n}} \\ = & 1+\frac{n}{1 !} \cdot \frac{1}{n}+\frac{n(n-1)}{2 !} \cdot \frac{1}{n^{2}}+\frac{n(n-1)(n-2)}{3 !} \cdot \frac{1}{n^{3}}+\cdots+ \\ & \frac{n(n-1)(n-2) \cdots(n-n+1)}{n !} \cdot \frac{1}{n^{n}} \\ = & 1+1+\frac{1}{2 !}\left(1-\frac{1}{n}\right)+\frac{1}{3 !}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)+\cdots+ \\ & \frac{1}{n !}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \cdots\left(1-\frac{n-1}{n}\right), \end{aligned}\tag{1.2.1} \end{equation}
又
\begin{equation} \begin{aligned} x_{n+1}= & 1+1+\frac{1}{2 !}\left(1-\frac{1}{n+1}\right)+\frac{1}{3 !}\left(1-\frac{1}{n+1}\right)\left(1-\frac{2}{n+1}\right)+\cdots+ \\ & \frac{1}{n !}\left(1-\frac{1}{n+1}\right)\left(1-\frac{2}{n+1}\right) \cdots\left(1-\frac{n-1}{n+1}\right)+ \\ & \frac{1}{(n+1) !}\left(1-\frac{1}{n+1}\right)\left(1-\frac{2}{n+1}\right) \cdots\left(1-\frac{n}{n+1}\right), \end{aligned}\tag{1.2.2} \end{equation}
比较(1.2.1)与(1.2.2), 从第 3 项起(1.2.1)的项小于(1.2.2)的对应项, 且(1.2.2)比(1.2.1)还多了最后一项 (正项), 所以 \(x_{n}<x_{n+1}\text{,}\) 即数列 \(\left\{x_{n}\right\}\) 单调增加.
\begin{equation*} \text { 又 } \begin{aligned} x_{n} & <1+1+\frac{1}{2 !}+\frac{1}{3 !}+\cdots+\frac{1}{n !}<1+1+\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\cdots+\frac{1}{(n-1) n} \\ & =1+1+\left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\cdots+\left(\frac{1}{n-1}-\frac{1}{n}\right)=3-\frac{1}{n}<3 . \end{aligned} \end{equation*}
即数列 \(\left\{x_{n}\right\}\) 有上界. 故由Proposition 1.2.48 得 \(\left\{x_{n}\right\}\) 收敛, 即 \(\lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}\) 存在. 上述这个极限通常用字母 e 表示, 即 \(\lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}=\mathrm{e}\text{.}\)
注意 数 \(\mathrm{e}\) 是个无理数, 它就是在 \(\mathbf{1 . 1 . 7}\) 中讲到的指数函数 \(y=\mathrm{e}^{x}\) 及自然对数 \(y=\ln x\) 中的底数 e. 数 e 在数学的理论研究与实际应用中都起着重要的作用. 一般地,可以证明
\begin{equation*} \lim\limits_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} \end{equation*}

Subsubsection 1.2.4.3 重要极限二 \(\lim\limits_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e}\text{.}\)

事实上,当 \(x \rightarrow+\infty\) 时, 设 \([x]=n\text{,}\) 则 \(n \leqslant x<n+1\text{,}\) 从而
\begin{equation*} \begin{gathered} \left(1+\frac{1}{n+1}\right)^{n}<\left(1+\frac{1}{x}\right)^{x}<\left(1+\frac{1}{n}\right)^{n+1} . \\ \lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{n}=\lim\limits_{n \rightarrow \infty}\left[\frac{\left(1+\frac{1}{n+1}\right)^{n+1}}{\left(1+\frac{1}{n+1}\right)}\right]=\mathrm{e}, \\ \lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n+1}=\lim\limits_{n \rightarrow \infty}\left[\left(1+\frac{1}{n}\right)^{n} \cdot\left(1+\frac{1}{n}\right)\right]=\mathrm{e}, \end{gathered} \end{equation*}
因为 所以由夹逼准则得
\begin{equation*} \lim\limits_{x \rightarrow+\infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} \end{equation*}
当 \(x \rightarrow-\infty\) 时, 令 \(u=-x\text{,}\) 则 \(u \rightarrow+\infty\text{.}\)
\begin{equation*} \left(1+\frac{1}{x}\right)^{x}=\left(1-\frac{1}{u}\right)^{-u}=\left(1+\frac{1}{u-1}\right)^{u}=\left(1+\frac{1}{u-1}\right)^{u-1}\left(1+\frac{1}{u-1}\right), \end{equation*}
于是
\begin{equation*} \lim\limits_{x \rightarrow-\infty}\left(1+\frac{1}{x}\right)^{x}=\lim\limits_{u \rightarrow+\infty}\left[\left(1+\frac{1}{u-1}\right)^{u-1} \cdot\left(1+\frac{1}{u-1}\right)\right]=\mathrm{e} . \end{equation*}
若令 \(t=\frac{1}{x}\text{,}\) 则当 \(x \rightarrow \infty\) 时, \(t \rightarrow 0\text{,}\) 从而有
\begin{equation*} \lim\limits_{t \rightarrow 0}(1+t)^{\frac{1}{t}}=\mathrm{e} . \end{equation*}
Example 1.2.54.
例 22 求 \(\lim\limits_{x \rightarrow \infty}\left(1-\frac{1}{x}\right)^{x}\text{.}\)
Solution.
解 \(\lim\limits_{x \rightarrow \infty}\left(1-\frac{1}{x}\right)^{x}=\lim\limits_{x \rightarrow \infty}\left[\left(1+\frac{1}{-x}\right)^{-x}\right]^{-1}=\mathrm{e}^{-1}\text{.}\)
Example 1.2.55.
例 23 求 \(\lim\limits_{x \rightarrow \infty}\left(\frac{3+x}{2+x}\right)^{2 x}\text{.}\)
Solution.
解 \(\lim\limits_{x \rightarrow \infty}\left(\frac{3+x}{2+x}\right)^{2 x}=\lim\limits_{x \rightarrow \infty}\left[\left(1+\frac{1}{x+2}\right)^{x}\right]^{2}=\lim\limits_{x \rightarrow \infty}\left[\left(1+\frac{1}{x+2}\right)^{x+2-2}\right]^{2}\)
\begin{equation*} =\lim\limits_{x \rightarrow \infty}\left[\left(1+\frac{1}{x+2}\right)^{x+2}\right]^{2}\left(1+\frac{1}{x+2}\right)^{-4}=\mathrm{e}^{2} \end{equation*}
Proposition 1.2.56 也称为柯西审敛原理 (它的证明超出本书的要求).
Example 1.2.57.
例 24 设 \(x_{n}=1-\frac{1}{2}+\frac{1}{3}-\cdots+(-1)^{n+1} \frac{1}{n}\text{,}\) 证明 \(\left\{x_{n}\right\}\) 收敛.
Solution.
证 对任给的 \(\varepsilon>0\text{,}\)对正整数 \(m>n\text{,}\) 要使
\begin{equation*} \left|x_{m}-x_{n}\right|=\frac{1}{n+1}-\frac{1}{n+2}+\cdots+(-1)^{m-n+1} \frac{1}{m}<\frac{1}{n+1}<\frac{1}{n}<\varepsilon, \end{equation*}
只要 \(n>\frac{1}{\varepsilon}\text{,}\) 可取 \(N=\left[\frac{1}{\varepsilon}\right]\text{,}\) 当 \(m, n>N\) 时,有 \(\left|x_{m}-x_{n}\right|<\varepsilon\text{,}\) 由柯西审敛原理Proposition 1.2.56 可知 \(\left\{x_{n}\right\}\) 收敛.
以后利用幂级数方法还可求得
\begin{equation*} \lim\limits_{n \rightarrow \infty}\left[1-\frac{1}{2}+\frac{1}{3}-\cdots+(-1)^{n+1} \frac{1}{n}\right]=\ln 2 \end{equation*}

Subsection 1.2.5 无穷小与无穷大

无穷小量与无穷大量在极限理论中起着重要的作用, 本节重点讨论无穷小的概念与无穷小量的阶.

Subsubsection 1.2.5.1 无穷小

Definition 1.2.58.
定义 8 在自变量的某种变化趋势下, 以零为极限的变量称为无穷小量, 简称无穷小.
例如, 当 \(x \rightarrow 0\) 时, \(x^{3}, \sin x, 1-\cos x\) 等是无穷小量; 当 \(x \rightarrow \infty\) 时, \(\frac{1}{x}, \mathrm{e}^{-x^{2}}\) 等是无穷小量; 当 \(n \rightarrow \infty\) 时, \(\frac{1}{n}, \sin \frac{1}{n}\) 等也是无穷小量. 无穷小量是一个变量, 它与自变量的变化过程有关, 如 \(x^{3}\) 当 \(x \rightarrow 0\) 时是无穷小量, 当 \(x \rightarrow 1\) 时不是无穷小量.
按照定义,零也是无穷小量, 并且是常量中唯一的无穷小量. 因为无穷小量是极限为零的变量, 所以无穷小量与有极限的量之间有着密切的联系.
Proof.
证 先证必要性. 设 \(\lim\limits_{x \rightarrow x_{0}} f(x)=A\text{.}\) 由极限运算法则
\begin{equation*} \lim\limits_{x \rightarrow x_{0}} \alpha(x)=\lim\limits_{x \rightarrow x_{0}}[f(x)-A]=\lim\limits_{x \rightarrow x_{0}} f(x)-A=A-A=0, \end{equation*}
所以 \(\alpha(x)=f(x)-A\) 当 \(x \rightarrow x_{0}\) 时为无穷小. 再证充分性. 由 \(\lim\limits_{x \rightarrow x_{0}} \alpha(x)=\lim\limits_{x \rightarrow x_{0}}[f(x)-A]=0\text{,}\)显然有
\begin{equation*} \lim\limits_{x \rightarrow x_{0}} f(x)=A \end{equation*}
\(x \rightarrow \infty\) 时的情形同理可证. 定理证毕.
因此,关系式 \(f(x)=A+\alpha(x)\) 给出了在某一变化过程中具有极限 \(A\) 的变量 \(f(x)\) 的重要表示法. 根据极限运算法则, 可得以下定理.
证明从略.
Example 1.2.61.
例 25 求 \(\lim\limits_{x \rightarrow 0}\left(x \cdot \sin \frac{1}{x}\right)\text{.}\)
Solution.
解 因为 \(\lim\limits_{x \rightarrow 0} x=0\text{,}\) 即当 \(x \rightarrow 0\) 时, \(x\) 为无穷小. 又因为 \(\left|\sin \frac{1}{x}\right| \leqslant 1\text{,}\) 即 \(\sin \frac{1}{x}\) 是有界函数. 所以, 由Theorem 1.2.60 得 \(\lim\limits_{x \rightarrow 0}\left(x \sin \frac{1}{x}\right)=0\text{.}\) 容易证明: 当 \(n \rightarrow \infty\) 时, \(\frac{1}{n} \sin n, \frac{1}{n}+\frac{1}{\sqrt{n}}, \frac{1}{n \sqrt{n}}\) 等是无穷小; 当 \(x \rightarrow \infty\) 时, \(\frac{1}{x} \sin x\text{,}\) \(\frac{1}{x}+\frac{1}{x^{2}}, \mathrm{e}^{-|x|}(1+\cos x+\sin x)\) 等是无穷小; 当 \(x \rightarrow x_{0}\) 时, \(\left(x-x_{0}\right)^{2}, \sin \left(x-x_{0}\right)\text{,}\) \(\left(x-x_{0}\right) \cos \frac{1}{x-x_{0}}\) 等是无穷小.

Subsubsection 1.2.5.2 无穷大

Definition 1.2.62.
定义 9 对于任意给定的正数 \(M\) (无论怎样大), 若存在 \(\delta>0\) (或 \(X>0\) ), 当 \(x \in \dot{U}\left(x_{0}, \delta\right)\) (或 \(\left.|x|>X\right)\) 时, 总有 \(|f(x)|>M\text{,}\) 则称 \(f(x)\) 当 \(x \rightarrow x_{0}\) (或 \(x \rightarrow \infty\) )时为无穷大量, 简称无穷大, 记作 \(\lim\limits_{x \rightarrow x_{0}} f(x)=\infty \left(\text{或 } \lim\limits_{x \rightarrow \infty} f(x)=\infty\right)\text{.}\)
类似地,可定义正负无穷大如下:
\begin{equation*} \begin{array}{ll} \lim\limits_{\substack{x \rightarrow x_{0} \\ (x \rightarrow \infty)}} f(x)=+\infty, & \lim\limits_{\substack{x \rightarrow x_{0} \\ (x \rightarrow \infty)}} f(x)=-\infty, \\ \lim\limits_{x \rightarrow x_{0}^{-}} f(x)=+\infty, & \lim\limits_{x \rightarrow x_{0}^{-}} f(x)=-\infty, \\ \lim\limits_{x \rightarrow x_{0}^{+}} f(x)=-\infty, & \lim\limits_{x \rightarrow x_{0}^{+}} f(x)=+\infty . \end{array} \end{equation*}
例如, \(\lim\limits_{x \rightarrow 0} \frac{1}{x}=\infty ; \lim\limits_{x \rightarrow \infty} x^{2}=+\infty\text{;}\) \(\lim\limits_{x \rightarrow \frac{\pi}{-}} \tan x=+\infty ; \lim\limits_{x \rightarrow \frac{\pi}{2}+} \tan x=-\infty\text{;}\) \(\lim\limits_{x \rightarrow 2} \frac{1}{x-2}=\infty\text{,}\)而 \(\lim\limits_{x \rightarrow \infty} \frac{1}{x-2}=0\) (见图 \(1-23\) ).
注意
  1. 无穷大是一个变量. 无穷大量是极限不存在的一种情形, 这里只是借用了极限记号, 但极限并不存在.
  2. 无穷大是无界的,但无界函数不一定是无穷大. 例如当 \(x \rightarrow \infty\) 时, \(x \sin x\) 无界,但不是无穷大.
无穷大与无穷小之间有着密切的联系.
Proof.
证 若 \(\lim\limits_{x \rightarrow x_{0}} f(x)=\infty\text{,}\) 根据定义任给 \(\varepsilon>0\text{,}\) 对于 \(M=\frac{1}{\varepsilon}\text{,}\) 存在 \(\delta>0\text{,}\) 当 \(0<\left|x-x_{0}\right|<\delta\text{,}\) 有
\begin{equation*} \begin{gathered} |f(x)|>M=\frac{1}{\varepsilon}, \\ \text{则}\hspace{1cm}\left|\frac{1}{f(x)}\right|<\varepsilon, \end{gathered} \end{equation*}
所以 \(\lim\limits_{x \rightarrow x_{0}} \frac{1}{f(x)}=0\text{,}\) 即 \(\frac{1}{f(x)}\) 为无穷小. 反之, 若 \(\lim\limits_{x \rightarrow x_{0}} \frac{1}{f(x)}=0\text{,}\) 且 \(f(x) \neq 0\text{.}\) 任给 \(M>0\text{,}\) 对于 \(\varepsilon=\frac{1}{M}\text{,}\) 由无穷小定义, 存在 \(\delta>0\text{,}\) 当 \(0<\left|x-x_{0}\right|<\delta,|f(x)|<\varepsilon=\frac{1}{M}\text{,}\) 即 \(\left|\frac{1}{f(x)}\right|>M\text{,}\) 所以 \(\frac{1}{f(x)}\) 为无穷大. 对于 \(x \rightarrow \infty\) 以及其他情形, 类似可证.
Example 1.2.64.
例 26 求 \(\lim\limits_{x \rightarrow 1} \frac{x^{5}-3 x+5}{x-1}\text{.}\)
Solution.
解 因为
\begin{equation*} \lim\limits_{x \rightarrow 1} \frac{x-1}{x^{5}-3 x+5}=\frac{0}{3}=0, \end{equation*}
所以
\begin{equation*} \lim\limits_{x \rightarrow 1} \frac{x^{5}-3 x+5}{x-1}=\infty . \end{equation*}

Subsubsection 1.2.5.3 无穷小的比较

两个无穷小的乘积是无穷小,但两个无穷小的商就不一定是无穷小了. 例如, 当 \(x \rightarrow 0\) 时, \(x, 2 x, x^{2}\) 都是无穷小, 但 \(\lim\limits_{x \rightarrow 0} \frac{x}{2 x}=\frac{1}{2}\text{,}\) \(\lim\limits_{x \rightarrow 0} \frac{x^{2}}{x}=0\text{,}\) \(\lim\limits_{x \rightarrow 0} \frac{x}{x^{2}}=\infty\text{.}\) 可见, 当 \(x \rightarrow 0\) 时, \(x\) 与 \(2 x\) 趋于零的快慢程度相当,而 \(x^{2}\) 比 \(x\) 趋于零的速度要快得多. 两个无穷小之比的极限情况, 反映出它们变化的“快慢”程度.
Definition 1.2.65.
定义 10 设 \(\alpha, \beta\) 在同一变化过程中是无穷小.
  1. 若 \(\lim \frac{\alpha}{\beta}=0\) 或 \(\lim \frac{\beta}{\alpha}=\infty\text{,}\) 则称 \(\alpha\) 为 \(\beta\) 的高阶无穷小,或 \(\beta\) 为 \(\alpha\) 的低阶无穷小, 记作 \(\alpha=o(\beta)\text{;}\)
  2. 若 \(\lim \frac{\alpha}{\beta}=C \neq 0\text{,}\)则称 \(\alpha\) 与 \(\beta\) 为同阶无穷小;
  3. 若 \(\lim \frac{\alpha}{\beta}=1\) 时,称 \(\alpha\) 与 \(\beta\) 为等价无穷小,记作 \(\alpha \sim \beta\text{;}\)
  4. 若 \(\lim \frac{\alpha}{\beta^{k}}=C \neq 0\text{,}\)则称 \(\alpha\) 是 \(\beta\) 的 \(k\) 阶无穷小.
例如, 因为 \(\lim\limits_{x \rightarrow 0} \frac{\sin x}{x}=1\text{,}\) 所以当 \(x \rightarrow 0\) 时, \(\sin x \sim x\text{.}\) 因为 \(\lim\limits_{x \rightarrow 0} \frac{\ln (1+x)}{x}=\lim\limits_{x \rightarrow 0} \ln (1+x)^{\frac{1}{x}}=\ln \mathrm{e}=1\text{,}\) 所以当 \(x \rightarrow 0\) 时, \(\ln (1+x) \sim x\text{.}\) 因为 \(\lim\limits_{x \rightarrow 0} \frac{\sin ^{2} x}{x}=0\text{,}\) 所以当 \(x \rightarrow 0\) 时, \(\sin ^{2} x\) 是比 \(x\) 高阶的无穷小. 因为 \(\lim\limits_{x \rightarrow 0} \frac{1-\cos x}{x^{2}}=\frac{1}{2}\text{,}\) 所以当 \(x \rightarrow 0\) 时 \(1-\cos x\) 是 \(x\) 的 2 阶无穷小. 因为 \(\lim\limits_{x \rightarrow 0} \frac{\sqrt[3]{2 x+x^{2}}}{x^{\frac{1}{3}}}=\sqrt[3]{2}\text{,}\) 所以当 \(x \rightarrow 0\) 时 \(\sqrt[3]{2 x+x^{2}}\) 是 \(x\) 的 \(\frac{1}{3}\) 阶无穷小. 注意 若 \(\lim \frac{\alpha}{\beta}\) 不存在,也不为 \(\infty\text{,}\)则 \(\alpha\) 与 \(\beta\) 不可比较. 例如, 当 \(x \rightarrow 0\) 时,无穷小 \(x\) 与无穷小 \(x \sin \frac{1}{x}\) 不可比较. 关于等价无穷小,有两个重要的定理.
事实上, 由 \(\frac{\beta}{\alpha}=1+\frac{o(\alpha)}{\alpha}\text{,}\) 利用Theorem 1.2.59 (有极限的量等于极限值与一个无穷小量之和), 容易得到本定理的结论.
Proof.
证 \(\lim \frac{\alpha}{\beta}=\lim \left(\frac{\alpha}{\alpha^{\prime}} \cdot \frac{\alpha^{\prime}}{\beta^{\prime}} \cdot \frac{\beta^{\prime}}{\beta}\right)=\lim \frac{\alpha}{\alpha^{\prime}} \cdot \lim \frac{\alpha^{\prime}}{\beta^{\prime}} \cdot \lim \frac{\beta^{\prime}}{\beta}=\lim \frac{\alpha^{\prime}}{\beta^{\prime}}\text{.}\)
本定理表明,求两个无穷小之比的极限, 其分子或分母都可以用它们的等价无穷小来代替.
Example 1.2.68.
例 27 求 \(\lim\limits_{x \rightarrow 0} \frac{\tan ^{2} x}{\sin \left(2 x^{2}\right)}\text{.}\)
Solution.
解 因为 \(\lim\limits_{x \rightarrow 0} \frac{\tan ^{2} x}{x^{2}}=1\text{,}\) 故当 \(x \rightarrow 0\) 时, \(\tan ^{2} x \sim x^{2}\text{.}\) 又 \(\lim\limits_{x \rightarrow 0} \frac{\sin \left(2 x^{2}\right)}{2 x^{2}}=1\text{,}\) 故当 \(x \rightarrow 0\) 时, \(\sin \left(2 x^{2}\right) \sim 2 x^{2}\text{.}\) 从而 \(\lim\limits_{x \rightarrow 0} \frac{\tan ^{2} x}{\sin \left(2 x^{2}\right)}=\lim\limits_{x \rightarrow 0} \frac{x^{2}}{2 x^{2}}=\frac{1}{2}\text{.}\)
Example 1.2.69.
例 28 求 \(\lim\limits_{x \rightarrow 0} \frac{a^{x}-1}{x}\text{.}\)
Solution.
解 令 \(t=a^{x}-1\text{,}\) 则 \(x=\frac{\ln (t+1)}{\ln a}\text{,}\) 当 \(x \rightarrow 0\) 时 \(t \rightarrow 0\text{.}\) 因为当 \(t \rightarrow 0\) 时,
\begin{equation*} \ln (1+t) \sim t, \end{equation*}
所以
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{a^{x}-1}{x}=\lim\limits_{t \rightarrow 0} \frac{t \ln a}{\ln (t+1)}=\ln a \end{equation*}
于是当 \(x \rightarrow 0\) 时, \(a^{x}-1 \sim x \ln a, \mathrm{e}^{x}-1 \sim x\text{.}\)
Example 1.2.70.
例 29 求 \(\lim\limits_{x \rightarrow 0} \frac{(1+x)^{\alpha}-1}{x}\text{.}\)
Solution.
解 令 \(t=(1+x)^{\alpha}-1\text{,}\) 则当 \(x \rightarrow 0\) 时, \(t \rightarrow 0\text{.}\) 因为当 \(t \rightarrow 0\) 时,
\begin{equation*} \ln (1+t) \sim t \end{equation*}
所以
\begin{equation*} (1+x)^{\alpha}-1 \sim \ln \left[1+(1+x)^{\alpha}-1\right]=\alpha \ln (1+x) \text {, } \end{equation*}
因此
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{(1+x)^{\alpha}-1}{x}=\lim\limits_{x \rightarrow 0} \frac{\alpha \ln (1+x)}{x}=\alpha . \end{equation*}
Example 1.2.71.
例 30 求 \(\lim\limits_{x \rightarrow 0} \frac{\tan x-\sin x}{\sin ^{3} 2 x}\text{.}\)
Solution.
错解 当 \(x \rightarrow 0\) 时, \(\tan x \sim x, \sin x \sim x\text{,}\) 所以
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{\tan x-\sin x}{\sin ^{3} 2 x}=\lim\limits_{x \rightarrow 0} \frac{x-x}{(2 x)^{3}}=0 . \end{equation*}
正解 当 \(x \rightarrow 0\) 时, \(\sin 2 x \sim 2 x, \tan x-\sin x=\tan x(1-\cos x) \sim \frac{1}{2} x^{3}\text{,}\) 故
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{\tan x-\sin x}{\sin ^{3} 2 x}=\lim\limits_{x \rightarrow 0} \frac{\frac{1}{2} x^{3}}{(2 x)^{3}}=\frac{1}{16} \end{equation*}
此例说明用等价无穷小替代求极限时, 只适用于乘除运算, 而不适用于加减运算.
Figure 1.2.72. 第一章第二节知识图谱

Subsection 1.2.6 习题

  1. 写出下列数列的前 5 项, 观察它们的变化趋势:
    1. \(x_{n}=\frac{2 n-1}{3 n+2}, n=1,2, \cdots\text{;}\)
    2. \(x_{n}=\frac{1-(-1)^{n}}{n^{3}}, n=1,2, \cdots\text{;}\)
    3. \(x_{n}=1+\frac{1}{2^{n}}, n=1,2, \cdots\text{;}\)
    4. \(x_{n}=\left(1+\frac{1}{n}\right)^{n}, n=1,2, \cdots\text{.}\)
  2. 用数列极限定义证明下列各题:
    1. \(\lim\limits_{n \rightarrow \infty} \frac{1}{n^{2}+3}=0\text{;}\)
    2. \(\lim\limits_{n \rightarrow \infty} \frac{2 n^{2}+3 n+5}{n^{2}+5 n+1}=2\text{;}\)
    3. \(\lim\limits_{n \rightarrow \infty} \frac{\sqrt{n^{2}+4}}{n}=1\text{;}\)
    4. \(\lim\limits_{n \rightarrow \infty} \frac{n !}{n^{n}}=0\text{;}\)
    5. \(\lim\limits_{n \rightarrow \infty}(\sqrt{n+1}-\sqrt{n})=0\text{;}\)
    6. \(\lim\limits_{n \rightarrow \infty}\left[\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\cdots+\frac{1}{(n-1) \times n}\right]=1\text{.}\)
  3. 求下列极限:
    1. \(\lim\limits_{n \rightarrow \infty} \frac{2 n-1}{5 n+4}\text{;}\)
    2. \(\lim\limits_{n \rightarrow \infty} \frac{3 n^{2}+n+5}{n^{3}+3 n+1}\text{;}\)
    3. \(\lim\limits_{n \rightarrow \infty}\left(\frac{3 n-5}{2 n+7}\right)^{6}\text{;}\)
    4. \(\lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n-1}\right)^{n}\text{;}\)
    5. \(\lim\limits_{n \rightarrow \infty} \frac{\sqrt{n}-8}{4 n+1}\text{;}\)
    6. \(\lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{2 n}\right)\left(3-\frac{1}{4 n}\right)\text{.}\)
  4. 设 \(\lim x_{n}=A \neq 0\text{,}\) 证明：
    1. \(\lim\limits_{n \rightarrow \infty} x_{n}^{2}=A^{2}\text{;}\)
    2. \(\lim\limits_{n \rightarrow \infty} \frac{1}{x_{n}}=\frac{1}{A}\text{.}\)
  5. 用函数极限定义证明下列各题:
    1. \(\lim\limits_{x \rightarrow-\frac{1}{2}} \frac{1-4 x^{2}}{2 x+1}=2\text{;}\)
    2. \(\lim\limits_{x \rightarrow 2} \frac{1+x}{2 x}=\frac{3}{4}\text{;}\)
    3. \(\lim\limits_{x \rightarrow 4} \sqrt{x}=2\text{;}\)
    4. \(\lim\limits_{x \rightarrow+\infty} \frac{1}{\sqrt{x}}=0\text{;}\)
    5. \(\lim\limits_{x \rightarrow \infty} \frac{3 x-1}{2 x+1}=\frac{3}{2}\text{;}\)
    6. \(\lim\limits_{x \rightarrow \infty} \frac{2-3 x}{x}=-3\text{.}\)
  6. 求下列极限:
    1. \(\lim\limits_{x \rightarrow 1} \frac{x^{2}-2 x+1}{x^{3}-1}\text{;}\)
    2. \(\lim\limits_{x \rightarrow-1} \frac{x^{2}+6 x+5}{1-x^{2}}\text{;}\)
    3. \(\lim\limits_{x \rightarrow 0} \frac{5 x^{3}+2 x^{2}-x}{3 x^{2}+2 x}\text{;}\)
    4. \(\displaystyle \lim\limits_{x \rightarrow 3} \frac{2 x^{2}-7 x+3}{x^{2}+4 x-21}\)
    5. \(\displaystyle \lim\limits_{x \rightarrow 1} \frac{x+x^{2}+\cdots+x^{n}-n}{x-1}\)
    6. \(\lim\limits_{x \rightarrow 0} \frac{(1+m x)^{n}-(1+n x)^{m}}{x^{2}} \quad(m, n\) 为正整数).
  7. 求下列极限:
    1. \(\lim\limits_{x \rightarrow \infty} \frac{3 x^{2}-1}{x^{2}-2 x+3}\text{;}\)
    2. \(\lim\limits_{x \rightarrow+\infty} \frac{\sqrt{x^{2}+1}}{x+1}\text{;}\)
    3. \(\lim\limits_{x \rightarrow \infty} \frac{[x]}{x}\text{;}\)
    4. \(\lim\limits_{x \rightarrow+\infty} \sqrt{x}(\sqrt{x+1}-\sqrt{x})\text{.}\)
  8. 证明:
    1. \(\lim\limits_{x \rightarrow \infty} f(x)=A\) 的充要条件是 \(\lim\limits_{x \rightarrow+\infty} f(x)=\lim\limits_{x \rightarrow-\infty} f(x)=A\text{;}\)
    2. \(\lim\limits_{x \rightarrow x_{0}} f(x)=A\) 的充要条件是 \(\lim\limits_{x \rightarrow x_{0}^{+}} f(x)=\lim\limits_{x \rightarrow x_{0}^{-}} f(x)=A\text{.}\)
  9. 设 \(\lim\limits_{x \rightarrow \infty}\left(\frac{x^{2}+1}{x+1}\right)-a x-b=0\text{,}\) 求常数 \(a, b\text{.}\)
  10. 设 \(f(x)=\left\{\begin{array}{ll}-a x+1, & 0 \leqslant x<1, \\ 1, & x=1, \\ -x+3, & 1<x \leqslant 2,\end{array}\right.\) 求 \(x \rightarrow 1\) 时函数的左、右极限, 并讨论极限的存在性.
  11. 函数 \(f(x)=\left\{\begin{array}{ll}\frac{\sin x}{x}, & x<0, \\ (1+x)^{\frac{1}{x}}, & x>0,\end{array}\right.\) 当 \(x \rightarrow 0\) 时极限是否存在?
  12. 求下列极限:
    1. \(\lim\limits_{x \rightarrow 0} \frac{\tan k x}{x}\) ( \(k\) 为常数);
    2. \(\lim\limits_{x \rightarrow 0^{+}} \frac{x}{\sqrt{1-\cos x}}\text{;}\)
    3. \(\lim\limits_{x \rightarrow 0} \frac{\tan x-\sin x}{x^{3}}\text{;}\)
    4. \(\displaystyle \lim\limits _{x \rightarrow 1}(1-x) \tan \frac{\pi x}{2}\)
    5. \(\lim\limits_{x \rightarrow 0} x \cot 2 x\text{;}\)
    6. \(\lim\limits _{x \rightarrow 0} \frac{\sqrt{2}-\sqrt{1+\cos x}}{\sin ^2 x}\text{;}\)
    7. \(\lim\limits_{n \rightarrow \infty} 2^{n} \sin \frac{x}{2^{n}}\text{;}\)
    8. \(\lim\limits _{n \rightarrow \infty} \frac{\sin \tan \frac{1}{n}}{\sin \frac{3}{n}}\text{.}\)
  13. 求下列极限:
    1. \(\lim\limits_{x \rightarrow \infty}\left(\frac{x}{1+x}\right)^{x}\text{;}\)
    2. \(\lim\limits _{x \rightarrow \infty}\left(\frac{3-2 x}{1-2 x}\right)^x\text{;}\)
    3. \(\lim\limits_{x \rightarrow 0}\left(1+\frac{x}{2}\right)^{\frac{x-1}{x}}\text{;}\)
    4. \(\lim\limits _{x \rightarrow \infty}\left(\frac{x^2}{x^2-1}\right)^x\text{.}\)
  14. 求下列极限:
    1. \(\lim\limits_{x \rightarrow 0} \frac{\sqrt{2+\tan x}-\sqrt{2+\sin x}}{x^{3}}\text{;}\)
    2. \(\lim\limits _{x \rightarrow \frac{\pi}{6}} \tan (3 x) \tan \left(\frac{\pi}{6}-x\right)\text{;}\)
    3. \(\lim\limits_{x \rightarrow \alpha} \frac{\sin x-\sin \alpha}{x-\alpha}\text{;}\)
    4. \(\lim\limits _{x \rightarrow \frac{\pi}{3}} \frac{1-2 \cos x}{\sin \left(x-\frac{\pi}{3}\right)}\text{.}\)
  15. 求下列极限:
    1. \(\lim\limits_{n \rightarrow \infty}\left[\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}}+\cdots+\frac{1}{(2 n)^{2}}\right]\text{;}\)
    2. \(\lim\limits_{n \rightarrow \infty}\left(1+2^{n}+3^{n}\right)^{1 / n}\text{.}\)
  16. 证明当 \(x \rightarrow 0\) 时, 下列无穷小等价:
    1. \(\arcsin (\tan x) \sim x\text{;}\)
    2. \(\arctan x \sim x\text{;}\)
    3. \(\mathrm{e}^{\sin x}-1 \sim x\text{;}\)
    4. \((1+\tan x)^{\alpha}-1 \sim \alpha x\) ( \(\alpha\) 为常数).
  17. 函数 \(f(x)=x \cos x\) 在 \((-\infty,+\infty)\) 内是否有界? 当 \(x \rightarrow \infty\) 时, \(f(x)\) 是否为无穷大?为什么?
  18. 当 \(x \rightarrow 0\) 时, 确定下列各无穷小的阶数:
    1. \(x^{3}+2 x^{2}\text{;}\)
    2. \(x^{5} \sin x^{3}\text{;}\)
    3. \(x-\sin x\text{;}\)
    4. \((\tan x)^{\frac{1}{3}}\text{;}\)
    5. \(1-\cos 2 x\text{;}\)
    6. \(\ln (1+\arcsin x)\text{.}\)
  19. 利用等价无穷小代换,求下列极限:
    1. \(\lim\limits_{x \rightarrow 0} \frac{\sin x^{3} \cos x}{\tan x-\sin x}\text{;}\)
    2. \(\displaystyle \lim\limits_{x \rightarrow 0} \frac{\sqrt{1+2 x^{2}}-1}{\sin \frac{x}{2} \arcsin x}\)
    3. \(\lim\limits_{x \rightarrow 0} \frac{\sin \left(x^{2} \sin \frac{1}{x}\right)}{x}\text{;}\)
    4. \(\lim\limits_{x \rightarrow 0} \frac{\sin x^{m}}{(\sin x)^{n}}(m, n\) 为正整数).
PrevTopNext