函数图形的描绘

Section 4.4 函数图形的描绘

Subsection 4.4.1 曲线的渐近线

曲线的渐近线是用来刻画曲线在无穷远处的状态.下面分别给出三种渐近线的定义及求法.

Subsubsection 4.4.1.1 水平渐近线和铅直渐近线

若 \(\lim\limits_{x \rightarrow \infty} f(x)=A\) ( \(A\) 为常数), 则称直线 \(y=A\) 为曲线 \(y=f(x)\) 的水平渐近线; 若 \(\lim\limits_{x \rightarrow x_{0}} f(x)=\infty\text{,}\) 则称直线 \(x=x_{0}\) 是曲线 \(y=f(x)\) 的铅直渐近线. 例如曲线 \(y=\frac{1}{x}\text{,}\) 因为 \(\lim\limits_{x \rightarrow \infty} \frac{1}{x}=0\text{,}\) 所以直线 \(y=0\text{,}\) 即 \(x\) 轴为其水平渐近线; 又 \(\lim\limits_{x \rightarrow 0} \frac{1}{x}=\infty\text{,}\) 所以直线 \(x=0\text{,}\)即 \(y\) 轴为其铅直渐近线; 这说明曲线在无穷远处分别无限接近两个坐标轴, 即随着 \(x\) 趋于 \(\infty\) 或趋于 0 ,曲线与 \(x\) 轴或 \(y\) 轴越来越接近.

Example 4.4.1.

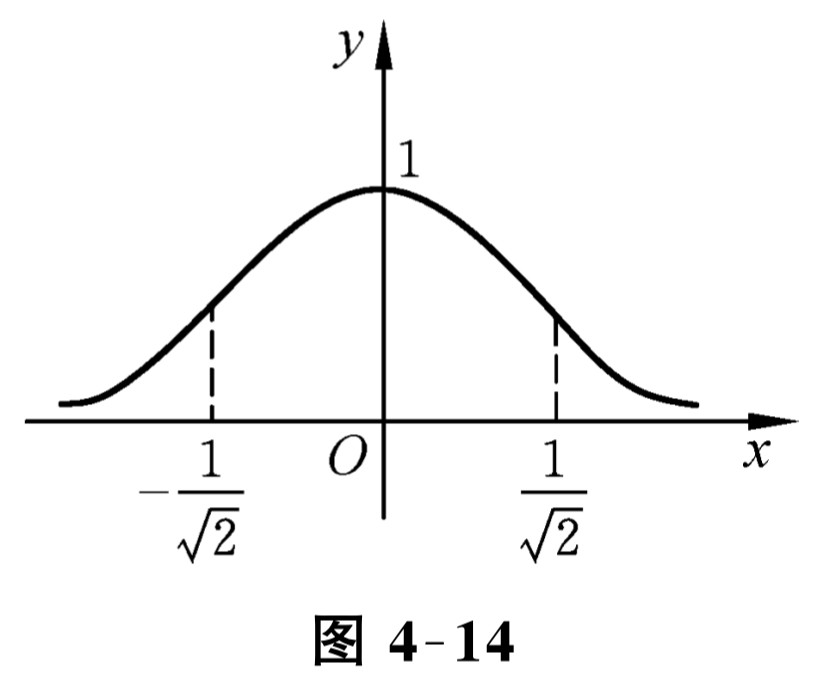
例 1 求曲线 \(y=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}}\) 的渐近线.

Solution.

解因为 \(\lim\limits_{x \rightarrow \infty} f(x)=\lim\limits_{x \rightarrow \infty} \frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}}=0\text{,}\) 所以 \(y=0\) 为该曲线的水平渐近线.

又因为 \(0 \leqslant y=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{x^{2}}{2}} \leqslant \frac{1}{\sqrt{2 \pi}}\text{,}\) 所以不可能有铅直渐近线.

这里需要注意的是并不是任何曲线都有渐近线.

Subsubsection 4.4.1.2 斜渐近线

若存在直线 \(y=k x+b\text{,}\) 使得 \(\lim\limits_{x \rightarrow \infty}[f(x)-k x-b]=0\text{,}\) 则称直线 \(y=k x+b\) 为 \(y=f(x)\) 的斜渐近线,此时表示曲线当 \(x \rightarrow \infty\) 时趋近于该直线.

容易验证直线 \(y=k x+b\) 为曲线 \(y=f(x)\) 的斜渐近线的充分必要条件是

\begin{equation*} k=\lim\limits_{x \rightarrow \infty} \frac{f(x)}{x}, b=\lim\limits_{x \rightarrow \infty}[f(x)-k x] . \end{equation*}

注意只要上述两个极限中有一个不存在, 都可以断定 \(y=f(x)\) 不存在斜渐近线.

Example 4.4.2.

例 2 求曲线 \(y=\frac{x^{2}}{x+1}\) 的渐近线.

Solution.

解因为 \(\lim\limits_{x \rightarrow-1} f(x)=\lim\limits_{x \rightarrow-1} \frac{x^{2}}{x+1}=\infty\text{,}\) 所以 \(x=-1\) 为该曲线的铅直渐近线.

又因为 \(\lim\limits_{x \rightarrow \infty} \frac{f(x)}{x}=\lim\limits_{x \rightarrow \infty} \frac{x^{2}}{x(x+1)}=1 ; \lim\limits_{x \rightarrow \infty}[f(x)-k x]=\lim\limits_{x \rightarrow \infty}\left(\frac{x^{2}}{x+1}-x\right)=-1\text{,}\)故直线 \(y=x-1\) 为曲线 \(y=\frac{x^{2}}{x+1}\) 的斜渐近线.

Subsection 4.4.2 函数图形的描绘

利用本章讨论过的函数的单调性、极值与曲线的凹凸性和拐点以及 4.4 .1 中给出的渐近线的求法, 并有选择地描出一些点, 就可以准确地描绘出函数的图形.描绘函数 \(y=f(x)\) 的图形的一般步骤如下: 第一,确定函数 \(y=f(x)\) 的定义域及函数的某些特征如奇偶性、周期性等; 第二, 求函数的一阶和二阶导数, 找出 \(f^{\prime}(x), f^{\prime \prime}(x)\) 等于零以及导数不存在的点, 用这些点将定义域划分为若干个区间; 第三, 确定所分区间中 \(f^{\prime}(x), f^{\prime \prime}(x)\) 的正负号, 列表讨论函数的单调性、极值、凹凸性和拐点等函数图形性质; 第四, 确定函数图形有无渐近线; 第五,适当定出图形上的几个点,绘图.

Example 4.4.3.

例 3 作函数 \(y=f(x)=\frac{x^{3}}{3}-2 x^{2}+3 x+1\) 的图形.

Solution.

解 (1) 定义域为 \((-\infty,+\infty)\text{.}\) (2)\(f^{\prime}(x)=x^{2}-4 x+3=(x-1)(x-3), f^{\prime \prime}(x)=2 x-4=2(x-2)\text{.}\) 令 \(f^{\prime}(x)=0, f^{\prime \prime}(x)=0\) 得到 \(x=1,2,3\text{.}\) 它们将 \((-\infty,+\infty)\) 分为 \((-\infty, 1)\text{,}\) \((1,2),(2,3),(3,+\infty)\text{,}\) 且算得 \(f(1)=\frac{7}{3}, f(2)=\frac{5}{3}, f(3)=1\text{.}\) (3)函数图形的性质: 单调性、极值、凹凸性、拐点等通过列表可以给出. Miss table****** （表中“ ”表示单调增加凸的; “ ”表示单调增加凹的; “〉”表示单调减少凸的; “”表示单调减少凹的)

(4)本题没有渐近线.

(5)选几个点, 由 \(f(0)=1, f(-1)=-\frac{13}{3}\text{,}\) \(f(4)=\frac{7}{3}\text{,}\) 即可定出点 \((0,1),\left(-1,-\frac{13}{3}\right),\left(4, \frac{7}{3}\right)\text{.}\)绘出图形 (见图 4-13).

Example 4.4.4.

例 4 作函数 \(y=\mathrm{e}^{-x^{2}}\) 的图形.

Solution.

解 (1) 定义域 \((-\infty,+\infty)\text{,}\) 并且 \(f(x)\) 为偶函数, 它的图形对称于 \(y\) 轴. 所以只需讨论 \((0,+\infty)\) 上该函数的图形,另一半由对称性可得到. (2)\(f^{\prime}(x)=-2 x \mathrm{e}^{-x^{2}}, f^{\prime \prime}(x)=-2\left(\mathrm{e}^{-x^{2}}-2 x^{2} \mathrm{e}^{-x^{2}}\right)=-2 \mathrm{e}^{-x^{2}}\left(1-2 x^{2}\right)\text{.}\) 令 \(f^{\prime}(x)=0, f^{\prime \prime}(x)=0\text{,}\) 解得 \(x=0, \pm \frac{1}{\sqrt{2}}\text{.}\) 并且 \(f(0)=1, f\left( \pm \frac{1}{\sqrt{2}}\right)=\mathrm{e}^{-\frac{1}{2}}\text{.}\) (3)列表, 给出函数的单调性、极值和函数图形的凹凸性、拐点等. Miss Table*******

(4)因为 \(\lim\limits_{x \rightarrow \infty} \mathrm{e}^{-x^{2}}=0\text{,}\) 所以直线 \(y=0\) 为水平渐近线.

(5)定出几个点, \((0,1),\left( \pm \frac{1}{\sqrt{2}}, \mathrm{e}^{-\frac{1}{2}}\right),( \pm 1\text{,}\) \(\mathrm{e}^{-1}\) ), 绘图, 如图 4-14 所示.

Example 4.4.5.

例 5 作函数 \(y=\frac{(x-1)^{3}}{x^{2}}\) 的图形.

Solution.

解 (1) 定义域为 \((-\infty, 0) \cup(0,+\infty)\text{.}\) (2)\(f^{\prime}(x)=\frac{(x-1)^{2}(x+2)}{x^{3}}, f^{\prime \prime}(x)=\frac{6(x-1)}{x^{4}}\text{.}\) 令 \(f^{\prime}(x)=0, f^{\prime \prime}(x)=0\text{,}\) 解得 \(x=-2,1\text{.}\) 将定义域分为 \((-\infty,-2),(-2\text{,}\) \(0),(0,1),(1,+\infty)\text{,}\) 且算得 \(f(-2)=-\frac{27}{4}, f(1)=0\text{.}\) (3)列表, 给出函数的单调性、极值和函数图形的凹凸性、拐点等. Miss table**** (4)因为 \(\lim\limits_{x \rightarrow 0} f(x)=-\infty\text{,}\) 所以直线 \(x=0\) 为铅直渐近线. 又因为 \(\lim\limits_{x \rightarrow \infty} \frac{f(x)}{x}=1 ; \lim\limits_{x \rightarrow \infty}[f(x)-x]=-3\text{.}\) 故直线 \(y=x-3\) 为曲线 \(y=\frac{(x-1)^{3}}{x^{2}}\) 的斜渐近线.

(5)绘图,如图 4-15 所示.

Subsection 4.4.3 习题 4- 4

按函数作图步骤, 作下列函数的图形:
1. \(y=x^{3}+6 x^{2}-15 x-20\text{;}\)
2. \(y=\frac{x^{3}}{2(1+x)^{2}}\text{;}\)
3. \(y=\frac{x^{2}}{x+1}\text{;}\)
4. \(y=x-2 \arctan x\text{;}\)
5. \(y=x \mathrm{e}^{-x}\text{;}\)
6. \(y=\ln \frac{1+x}{1-x}\text{;}\)
7. \(y=\frac{(x-3)^{2}}{4(x-1)}\text{;}\)
8. \(y=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-\frac{(x-a)^{2}}{2 \sigma^{2}}} \quad(a, \sigma>0)\text{.}\)

Prev Top Next