Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 4.2 函数的单调性和极值

Subsection 4.2.1 函数的单调性

为了研究函数和曲线的性态, 首先考虑函数的单调性质. 函数 \(f(x)\) 的单调性和自变量 \(x\) 的取值范围有关. 在第 1 章中已给出函数单调性的定义,但是用定义直接判断一个函数在所给区间上单调增加或单调减少是很困难的, 这里将借助函数导数的符号来判断函数的单调性. 设函数 \(f(x)\) 在 \([a, b]\) 上连续, 在 \((a, b)\) 内可导. 观察图 4-1 及图 4-2.
图 4-1 中曲线所表示的函数 \(y=f(x)\) 是单调增加函数, 注意到图形中曲线的切线的斜率为正数, 即 \(f^{\prime}(x) \geqslant 0\text{.}\) 图 4-2 中曲线表示的函数是单调减少函数,而曲线上任一点的切线斜率为负数, 即 \(f^{\prime}(x) \leqslant 0\left(f^{\prime}(x)=0\right.\) 只有在个别点上成立).从这两个图形中, 发现对可导函数在一个区间上的单调性与其一阶导数的符号有关. 于是反过来考虑函数 \(y=f(x)\) 的单调性能否用它的导数来判断呢? 函数单调性判定定理如下.

Proof.

证 (1) 在 \([a, b]\) 上任取两点 \(x_{1}, x_{2}\) (不妨设 \(x_{1}<x_{2}\) ), 在闭区间 \(\left[x_{1}, x_{2}\right]\) 上应用拉格朗日中值定理,得
\begin{equation*} f\left(x_{2}\right)-f\left(x_{1}\right)=f^{\prime}(\xi)\left(x_{2}-x_{1}\right) \quad\left(x_{1}<\xi<x_{2}\right) . \end{equation*}
上式中因为 \(f^{\prime}(\xi)>0, x_{2}-x_{1}>0\text{,}\) 从而 \(f\left(x_{2}\right)-f\left(x_{1}\right)>0\text{,}\) 即 \(f\left(x_{2}\right)>\) \(f\left(x_{1}\right)\text{.}\) 因为 \(x_{1}, x_{2}\) 在 \([a, b]\) 上的任意性,所以 \(f(x)\) 在 \([a, b]\) 上单调增加. 用同样的方法,可证明单调减少的情形。
Theorem 4.2.1表明,要找出可导函数的单调区间, 只要求出这个函数的导数, 再根据它的符号就能确定函数的单调区间, 且对可导函数来讲,在单调区间的分界点 \(x_{0}\)处 \(f^{\prime}\left(x_{0}\right)=0\text{.}\) 用这些导数的零点来划分定义域, 就是函数的单调区间. 若函数在某些点处不可导,则用来划分函数定义域的分界点还应包括这些导数不存在的点. 因此可按下述步骤讨论函数的单调性:
  1. 确定连续函数 \(f(x)\) 的定义域;
  2. 求出 \(f^{\prime}(x)=0\) 的根及 \(f^{\prime}(x)\) 不存在的点, 按这些点从小到大的顺序将定义域分成若干个区间;
  3. 判断 \(f^{\prime}(x)\) 在每个区间内的符号, 就可确定函数 \(f(x)\) 的单调性.
在Theorem 4.2.1 中如果将闭区间 \([a, b]\) 换为开区间,那么Theorem 4.2.1 的结果仍然成立. 习惯上单调区间都写成开区间的形式 (即略去端点). 一般地, 若 \(f^{\prime}(x)\) 在某区间内有限个点处为零, 其余各点处均为正 (或负) 时,Theorem 4.2.1 的结果仍然成立.

Example 4.2.2.

例 1 讨论 \(y=\arctan x-x\) 的单调性.
Solution.
解 \(y^{\prime}=\frac{1}{1+x^{2}}-1=\frac{-x^{2}}{1+x^{2}} \leqslant 0\text{.}\) 当 \(x \in(-\infty,+\infty)\) 时, \(y^{\prime} \leqslant 0\text{,}\) 等号仅在 \(x=0\)处成立. 所以 \(y=\arctan x-x\) 在区间 \((-\infty,+\infty)\) 上单调减少.

Example 4.2.3.

例 2 确定函数 \(f(x)=2 x^{3}-9 x^{2}+12 x-3\) 的单调区间.
Solution.
解 该函数在其定义区间 \((-\infty,+\infty)\) 上连续,且有连续导数
\begin{equation*} f^{\prime}(x)=6 x^{2}-18 x+12=6(x-1)(x-2) . \end{equation*}
令 \(f^{\prime}(x)=0\text{,}\) 得 \(x=1,2\text{.}\) 从而使 \(f^{\prime}(x)=0\) 的点只有有限个 (两个), 并且在区间 \((-\infty, 1)\) 内 \(f^{\prime}(x)>0\text{;}\) 在区间 \((1,2)\) 内 \(f^{\prime}(x)<0\text{;}\) 在区间 \((2,+\infty)\) 内 \(f^{\prime}(x)>0\text{.}\) 所以函数在区间 \((-\infty, 1)\) 和 \((2,+\infty)\) 内单调增加,在区间 \((1,2)\) 内单调减少.
现将上述讨论用表格表述如下: ***** 函数 \(y=f(x)\) 的图形如图 4-3 所示.

Example 4.2.4.

例 3 证明下列不等式:
  1. 当 \(x>1\) 时, \(\ln x>\frac{2(x-1)}{x+1}\text{;}\)
  2. 当 \(x \in(0,1)\) 时， \((1+x) \ln ^{2}(1+x)<x^{2}\text{.}\)
Solution.
证 (1) 令 \(f(x)=\ln x-\frac{2(x-1)}{x+1}\text{,}\) 则当 \(x>1\) 时,有
\begin{equation*} f^{\prime}(x)=\frac{1}{x}-\frac{4}{(x+1)^{2}}=\frac{(x-1)^{2}}{x(x+1)^{2}}>0 . \end{equation*}
所以当 \(x>1\) 时, \(f^{\prime}(x)>0, f(x)\) 单调增加. 因此 \(f(x)>\) \(f(1)=0\text{,}\) 于是有 \(\ln x-\frac{2(x-1)}{x+1}>0\text{.}\) 证毕.
(2) 令 \(f(x)=x^{2}-(1+x) \ln ^{2}(1+x)\text{,}\) 则在 \(x \in(0,1)\) 内
\begin{equation*} f^{\prime}(x)= 2 x-\ln ^{2}(1+x)-2 \ln (1+x), \end{equation*}
\begin{equation*} f^{\prime \prime}(x)= 2-\frac{2 \ln (1+x)}{1+x}-\frac{2}{1+x}=\frac{2}{1+x}[x-\ln (1+x)]>0, \end{equation*}
因为对任意的 \(x>0, \ln (1+x)<x\text{,}\) 由此得 \(x>0\) 时, \(f^{\prime}(x)\) 为单调增加. 又 \(f^{\prime}(0)=\) 0 , 则 \(f^{\prime}(x)>0\text{.}\) 所以当 \(x>0\) 时, \(f(x)\) 单调增加. 又 \(f(0)=0\text{,}\) 则 \(f(x)>0\text{,}\) 即
\begin{equation*} (1+x) \ln ^{2}(1+x)<x^{2} . \end{equation*}

Subsection 4.2.2 函数的极值

通常如果某个函数在其定义区间内既有单调增加的部分又有单调减少的部分,那么曲线段就会在某些点处呈现出如山峰的顶或山谷的底 (见图 4-4),
\(x=x_{2}, x_{4}\) 点处曲线段为峰顶, 而 \(x=x_{1}, x_{3}, x_{5}\) 点处的曲线段为谷底. 在这些点处的函数值总是比它们左右邻近点处的函数值大或小. 在Example 4.2.3 中, \(x=1\) 左右邻近点处的函数值比 \(x=1\) 的函数值小, \(x=2\) 处左右邻近点处的函数值比 \(x=2\) 处的函数值大. 称 \(x=1\) 处的函数值 \(f(1)\) 为极大值, \(x=2\) 处的函数值 \(f(2)\) 为极小值. 下面给出函数极值的严格定义.
定义 设 \(f(x)\) 在 \(x_{0}\) 的某邻域 \(U\left(x_{0}\right)\) 内有定义,若对任一 \(x \in \dot{U}\left(x_{0}\right)\text{,}\) 有 \(f(x)<f\left(x_{0}\right)\text{,}\) 则称 \(x_{0}\) 为 \(f(x)\) 的极大值点, \(f\left(x_{0}\right)\) 为 \(f(x)\) 的一个极大值; 若对任一 \(x \in \dot{U}\left(x_{0}\right)\text{,}\) 有 \(f(x)>f\left(x_{0}\right)\text{,}\) 则称 \(x_{0}\) 为 \(f(x)\) 的极小值点, \(f\left(x_{0}\right)\) 为 \(f(x)\) 的一个极小值. 极大值、极小值统称为极值. 使函数取得极值的点统称为极值点. 注意 函数的极值是函数在局部范围内的性质, 仅在某点的邻域内进行考 虑. 如图 4-4 所示, 函数 \(y=f(x)\) 中的 \(x_{1}, x_{3}, x_{5}\) 是 \(f(x)\) 的极小值点, \(x_{2}, x_{4}\) 是 \(f(x)\) 的极大值点, 在同一函数中, 极小值可能大于它的极大值 (如图 4-4 中, \(f\left(x_{2}\right)<\) \(f\left(x_{5}\right)\) ). 如果按定义来寻求 \(f(x)\) 的极值往往是很困难的. 但是, 由图 4-4 可以发现, 极值点是函数由单调增加变为单调减少或由单调减少变为单调增加的转折点, 即 \(f^{\prime}(x)\) 经 \(f^{\prime}\left(x_{0}\right)\) 后由正变负或由负变正,所以推出 \(f^{\prime}\left(x_{0}\right)=0\text{.}\) 下面讨论函数取得极值的必要条件和充分条件.
Theorem 4.2.5 就是上一章的费马引理. 通常称一阶导数为零的点 (即 \(f^{\prime}(x)=0\) 的实根) 为函数的驻点. 由Theorem 4.2.5得到: 可导函数的极值点必定是它的驻点. 但反之不成立, 函数的驻点却不一定是极值点. 例如, \(f(x)=x^{3}, f^{\prime}(x)=3 x^{2}\text{,}\) 由于 \(f^{\prime}(x)>0\text{,}\) 所以 \(f(x)=x^{3}\) 在全区间 \((-\infty,+\infty)\) 上是单调上升的, 且当 \(x=0\) 时 \(f^{\prime}(x)=0, x=0\) 是这个函数的驻点,但不是极值点. 从而某点处的导数为 0 是可导函数在该点取得极值的必要条件,而不是充分条件. 注意,在导数不存在的点处, 函数也可能取得极值. 例如, \(f(x)=|x|\text{,}\) 由第 3 章得到函数在 \(x=0\) 处导数不存在,但 \(x=0\) 是函数的极小值点, 函数在该点取得极小值 \(f(0)=0\text{.}\) 从而, 函数的极值点一定是函数的驻点或导数不存在的点, 统称这两种点为极值点的嫌疑点. 由于嫌疑点可能是极值点, 也可能不是极值点, 那么应如何判别嫌疑点是否为极值点呢? 下面给出判别函数极值点的两个充分条件.

Proof.

证 (1) 设 \(x_{1}\) 为定理条件中所给邻域中的任意一点,由拉格朗日中值定理得
\begin{equation*} f\left(x_{1}\right)-f\left(x_{0}\right)=f^{\prime}(\xi)\left(x_{1}-x_{0}\right), \xi \text { 在 } x_{1} \text { 与 } x_{0} \text { 之间. } \end{equation*}
若 \(x_{1}<x_{0}\text{,}\) 则 \(x_{1}<\xi<x_{0}\text{,}\) 即 \(\xi\) 在所给邻域的左半部分, 由条件知 \(f^{\prime}(\xi)>0\text{,}\) 从而 \(f\left(x_{1}\right)-f\left(x_{0}\right)<0\text{,}\) 即 \(f\left(x_{1}\right)<f\left(x_{0}\right)\text{.}\) 若 \(x_{1}>x_{0}\text{,}\) 则 \(x_{0}<\xi<x_{1}\text{,}\) 即 \(\xi\) 在所给邻域的右半部分, 由条件知 \(f^{\prime}(\xi)<0\text{,}\) 从而 \(f\left(x_{1}\right)-f\left(x_{0}\right)<0\text{,}\) 即 \(f\left(x_{1}\right)<f\left(x_{0}\right)\text{.}\) 因此,对任意 \(x \in \dot{U}\left(x_{0}\right)\text{,}\) 均有 \(f(x)<f\left(x_{0}\right)\text{,}\) 所以 \(x_{0}\) 为极大值点. 类似于 (1) 可以证明 (2). （3）由于在所给邻域内不论是 \(x<x_{0}\) 还是 \(x>x_{0}, f^{\prime}(x)\) 符号相同, 在该邻域内 \(f(x)\) 总是单调增加或是单调减少, 所以 \(x_{0}\) 不是极值点.
Theorem 4.2.6可简单地叙述为: 在嫌疑点 \(x_{0}\) 的左右, 若函数 \(f(x)\) 的导数 \(f^{\prime}(x)\) 变号,则 \(x_{0}\) 是极值点,否则 \(x_{0}\) 就不是极值点.

Example 4.2.7.

例 4 求函数 \(f(x)=x^{3}-3 x^{2}-9 x+5\) 的极值.
Solution.
解 第一步, 求驻点及导数不存在的点. 由
\begin{equation*} f^{\prime}(x)=3 x^{2}-6 x-9=3(x+1)(x-3), \end{equation*}
令 \(f^{\prime}(x)=0\text{,}\) 得驻点 \(x=-1, x=3\text{.}\) (本题中没有导数不存在的点)
第二步, 利用驻点及导数不存在的点, 将函数的定义域分成若干区间. 本题 \(f(x)\) 的定义域为 \((-\infty,+\infty)\text{,}\) 用驻点将区间分成如下三个区间:
\begin{equation*} (-\infty,-1),(-1,3),(3,+\infty) . \end{equation*}
第三步, 在各区间上, 判别 \(f^{\prime}(x)\) 的符号, 并判断驻点及导数不存在点是否为极值点. 通常, 列表给出 \(f^{\prime}(x)\) 的符号.****
表格中很清楚地显示出各区间内 \(f^{\prime}(x)\) 的符号及函数的单调增加和单调减少的性质, 由Theorem 4.2.6 很容易从表格中判断出 \(x=-1\) 是极大值点, \(f(-1)=10\) 是极大值, \(x=3\) 是极小值点, \(f(3)=-22\) 是极小值.
当函数 \(f(x)\) 在驻点处的二阶导数存在且不为零时, 可以使用下面的定理来判定 \(f(x)\) 在驻点处是否取得极值.

Proof.

证 (1) 因为 \(f^{\prime \prime}\left(x_{0}\right)<0\text{,}\) 按照二阶导数的定义有
\begin{equation*} f^{\prime \prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}} \frac{f^{\prime}(x)-f^{\prime}\left(x_{0}\right)}{x-x_{0}}<0 . \end{equation*}
由 1.2.2 函数的极限性质得到, 在 \(x_{0}\) 的某个去心邻域内, 有
\begin{equation*} \frac{f^{\prime}(x)-f^{\prime}\left(x_{0}\right)}{x-x_{0}}<0 \end{equation*}
成立.
因为 \(f^{\prime}\left(x_{0}\right)=0\text{,}\) 所以 \(\frac{f^{\prime}(x)}{x-x_{0}}<0\text{.}\) 从而, 对于该邻域内不同于 \(x_{0}\) 的 \(x\) 来说, \(f^{\prime}(x)\) 与 \(x-x_{0}\) 符号相反. 因此, 若 \(x-x_{0}<0\text{,}\) 即 \(x<x_{0}\) 时, \(f^{\prime}(x)>0\text{;}\) 若 \(x-x_{0}>0\text{,}\)即 \(x>x_{0}\) 时, \(f^{\prime}(x)<0\text{.}\) 由Theorem 4.2.6 知, \(f(x)\) 在点 \(x_{0}\) 处取得极大值.
类似可以证明 (2).

Example 4.2.9.

例 5 求 \(f(x)=\mathrm{e}^{x} \cos x\) 的极值.
Solution.
解 \(f^{\prime}(x)=\mathrm{e}^{x} \cos x-\mathrm{e}^{x} \sin x\text{.}\)
令 \(f^{\prime}(x)=0\text{,}\) 得驻点 \(x=k \pi+\frac{\pi}{4}, k\) 为整数. 由于 \(f^{\prime \prime}(x)=-2 \mathrm{e}^{x} \sin x\text{,}\) 当 \(x=2 k \pi+\frac{\pi}{4}\)时, \(f^{\prime \prime}(x)<0\text{,}\) 所以 \(x=2 k \pi+\frac{\pi}{4}\) 为极大值点, 函数的极大值为 \(f\left(2 k \pi+\frac{\pi}{4}\right)=\) \(\frac{\sqrt{2}}{2} \mathrm{e}^{2 k \pi+\frac{\pi}{4}}\text{;}\) 当 \(x=\left[(2 k+1) \pi+\frac{\pi}{4}\right]\) 时, \(f^{\prime \prime}(x)>0\text{,}\) 所以 \(x=\left[(2 k+1) \pi+\frac{\pi}{4}\right]\) 为极小值点, 函数的极小值为 \(f\left[(2 k+1) \pi+\frac{\pi}{4}\right]=-\frac{\sqrt{2}}{2} \mathrm{e}^{(2 k+1) \pi+\frac{\pi}{4}}(k=0, \pm 1, \pm 2, \cdots)\text{.}\)
总结以上各例题的解题过程, 求极值的步骤如下:
  1. 求函数的导数;
  2. 求导数的零点 (即驻点) 及导数不存在的点;
  3. 应用Theorem 4.2.6或Theorem 4.2.8 判定驻点及导数不存在的点是否为极值点, 从而求出极值.

Subsection 4.2.3 最大值和最小值问题

函数的最大值、最小值是函数在定义域全局范围内的性质. 在许多实际问题中常常会遇到各种各样的求某个函数的最大值或最小值的问题, 本节探讨最大值及最小值的求法及其应用.
假设函数 \(y=f(x)\) 在 \([a, b]\) 上连续, 根据闭区间上连续函数的性质, \(f(x)\) 在 \([a, b]\) 上必能取得最大值和最小值. 如果最大值 (或最小值) 在区间 \((a, b)\) 内部取得, 那么这个最大值 (或最小值)一定也是函数的极大值 (或极小值). 但最大值 (或最小值) 也可能在区间的端点取得. 因此, 通过比较 \(f(x)\) 在开区间 \((a, b)\) 内的所有极值及在区间的两个端点处函数值 \(f(a), f(b)\) 的大小, 就可以求出 \(f(x)\) 在 \([a, b]\) 上的最大值 (或最小值).
如图 4-5 所 示, \(f(x)\) 在 \([a, b]\) 上连续, 在 \(x_{3}\) 处不可导, 在 \((a, b)\) 内极值点为 \(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\text{,}\) 端点为 \(a, b\) 两点. 比较各点的函数值的大小, 得到函数在 \(x=b\) 处取得最小值, 在 \(x=\) \(x_{1}\) 处取得最大值.
通常, 对 \([a, b]\) 上的连续函数,也可以避免考虑在 \((a, b)\) 内的极值点, 只需求出 \((a, b)\) 内所有嫌疑点的函数值及两端点处的函数值, 再比较其大小, 即可得到函数的最大值和最小值. 当 \(y=f(x)\) 在它的取值范围内, 只有一个极值时, 这个极值若是极大 (极小)值, 则其就是函数的最大 (最小) 值.

Example 4.2.10.

例 6 求函数 \(f(x)=x^{4}-8 x^{2}-2\) 在 \([-1,4]\) 上的最大值和最小值.
Solution.
解 令 \(f^{\prime}(x)=4 x^{3}-16 x=4 x\left(x^{2}-4\right)=4 x(x-2)(x+2)=0\text{,}\) 求得驻点 \(x=0\text{,}\) \(-2,2\text{.}\) 因 \(x=-2\) 不在定义域中,故舍去. 比较驻点及区间端点函数值的大小, 因为 \(f(0)=-2, f(2)=-18, f(-1)=-9, f(4)=126\text{.}\)
因此, \(f(x)\) 在 \(x=2\) 处取得最小值 -18 , 在 \(x=4\) 处取得最大值 126 .

Example 4.2.11.

例 7 证明不等式 \(x^{\alpha}-\alpha x \leqslant 1-\alpha \quad(x>0,0<\alpha<1)\text{.}\)
Solution.
解 设 \(f(x)=x^{\alpha}-\alpha x-(1-\alpha)\text{,}\) 则 \(f^{\prime}(x)=\alpha x^{\alpha-1}-\alpha=\alpha\left(x^{\alpha-1}-1\right)\text{.}\)令 \(f^{\prime}(x)=0\text{,}\) 得唯一驻点 \(x=1\text{.}\) 当 \(0<x<1\) 时, \(f^{\prime}(x)>0\text{;}\) 当 \(x>1\) 时, \(f^{\prime}(x)<0\text{,}\) 则 \(f(1)\)是 \(f(x)\) 在 \((0,+\infty)\) 内的最大值, 即有 \(f(x) \leqslant f(1)=0\text{,}\) 从而 \(x^{\alpha}-\alpha x-(1-\alpha) \leqslant 0\text{,}\)即 \(x^{\alpha}-\alpha x \leqslant 1-\alpha \quad(x>0,0<\alpha<1)\text{.}\)
求实际问题中的最大值与最小值, 是实践中经常会遇到的问题. 在求实际问题中的最大值、最小值问题时, 首先要把需要解决的实际问题转化为数学问题, 根据实际情况, 建立它的数学模型, 并确定实际变量的变化范围. 由于实际问题中的函数通常是可导的, 所以实际问题中的最大值和最小值往往在驻点及函数变化的区间端点处取得, 如果函数的变化范围是开区间, 那么最大值和最小值从驻点处取得.

Example 4.2.12.

例 8 以直的河岸为一边用篱笆围出一块矩形场地, 现有 \(36 \mathrm{~m}\) 长的篱笆, 问所能围出的最大场地面积是多少?
Solution.
解 由题意, 假定矩形场地中与河岸垂直的边长为 \(x \mathrm{~m}\text{,}\) 则另一边长为 \((36-2 x) \mathrm{m}\text{,}\) 如图 4-6 所示, 设矩形场地面积为 \(S \mathrm{~m}^{2}\text{,}\) 则
\begin{equation*} \begin{gathered} S=x(36-2 x)=36 x-2 x^{2}, 0<x<\frac{36}{2}=18 . \\ S^{\prime}(x)=36-4 x, \text { 令 } S^{\prime}(x)=0, \text { 得 } x=9 . \end{gathered} \end{equation*}
\(x=9\) 为唯一驻点, 从本题的实际意义得到, 该矩形场地面积确有最大值, 从而这个唯一驻点的函数值一定是最大值. 也可以利用极值的充分条件判别它是开区间 \((0,18)\) 内的极大值, 因为 \(S^{\prime \prime}(x)=-4, S^{\prime \prime}(9)<0\text{,}\) 所以 \(x=9\) 是极大值点. 故 \(S(9)\) 就是 \(x \in(0,18)\) 内的最大值. 因此, 所围出的场地一边为 9 , 另一边为 18 时,场地面积最大,且最大面积为 \(9 \times 18=162 \mathrm{~m}^{2}\text{.}\)

Example 4.2.13.

例 9 要建造一个有一定容积 \(V\) 的无底的圆柱形煤气罐, 问怎样选择它的直径 \(d\) 和高 \(h\) (见图 4-7), 才能使所用的材料最省?
Solution.
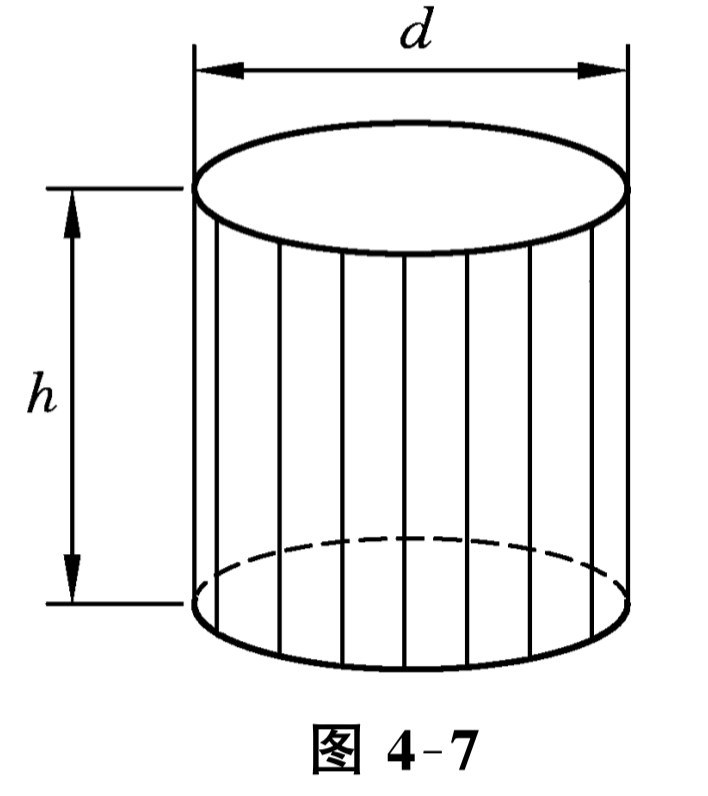
解 由题意, 要求材料最省, 就是指煤气罐的表面积最小. 记表面积为 \(S\text{,}\) 因为
\begin{equation*} V=\pi\left(\frac{d}{2}\right)^{2} h \end{equation*}
所以 \(h=\frac{4 V}{\pi d^{2}}\text{.}\) 又由于煤气罐无底, 所以煤气罐的表面积 \(S=\pi d h+\pi\left(\frac{d}{2}\right)^{2}\text{,}\) 从而得
\begin{equation*} \begin{gathered} S=\frac{4 V}{d}+\frac{\pi}{4} d^{2}, 0<d<+\infty, \\ S^{\prime}(d)=-\frac{4 V}{d^{2}}+\frac{\pi}{2} d, \end{gathered} \end{equation*}
令 \(S^{\prime}(d)=0\text{,}\) 解得 \(d=2 \sqrt[3]{\frac{V}{\pi}}\text{.}\)
这是表面积函数的唯一的驻点. 由实际问题的意义, 可以断定最小值一定存在,从而这个驻点处的函数值就是最小值, 即当直径 \(d=2 \sqrt[3]{V / \pi}\text{,}\) 高 \(h=\frac{4 V}{\pi(2 \sqrt[3]{V / \pi})^{2}}=\) \(\sqrt[3]{V / \pi}(\) 即 \(d=2 h\) ) 时建造煤气罐所用材料最省.

Subsection 4.2.4 习题 4-2

  1. 求下列函数的单调区间:
    1. \(y=x^{3}-3 x^{2}-9 x+14\text{;}\)
    2. \(y=\frac{x}{1+x^{2}}\text{;}\)
    3. \(y=\sqrt{2 x-x^{2}}\text{;}\)
    4. \(y=x-2 \sin x(0 \leqslant x \leqslant 2 \pi)\text{;}\)
    5. \(y=x-\ln (1+x)\text{;}\)
    6. \(y=x-\mathrm{e}^{x}\text{.}\)
  2. 证明: 若函数 \(f(x)\) 和 \(g(x)\) 在 \(a\) 点连续,在 \((a, b)\) 内可导,且当 \(f(a)=g(a), x \in(a, b)\) 时 \(f^{\prime}(x)>g^{\prime}(x)\text{,}\) 则 \(x \in(a, b)\) 时 \(f(x)>g(x)\text{.}\)
  3. 证明下列不等式:
    1. \(x>1\) 时, \(2 \sqrt{x}>3-\frac{1}{x}\text{;}\)
    2. \(x>0\) 时, \(\ln (1+x)>\frac{\arctan x}{1+x}\text{;}\)
    3. \(0<x<\frac{\pi}{2}\) 时, \(\tan x>x+\frac{x^{3}}{3}\text{;}\)
    4. \(x>0\) 时, \(1-x+\frac{x^{2}}{2}>\mathrm{e}^{-x}>1-x\text{;}\)
    5. \(x>0\) 时, \(x-\frac{x^{2}}{2}<\ln (1+x)<x\text{.}\)
  4. 求下列函数的极值:
    1. \(y=\frac{(x-2)(x-3)}{x^{2}}\text{;}\)
    2. \(y=\sqrt[3]{\left(x^{2}-a^{2}\right)^{2}}\) ( \(a\) 为正常数);
    3. \(y=x+\sqrt{1-x}\text{;}\)
    4. \(y=\cos x+\sin x\left(-\frac{\pi}{2} \leqslant x \leqslant \frac{\pi}{2}\right)\text{;}\)
    5. \(y=x^{2} \mathrm{e}^{-x^{2}}\text{;}\)
    6. \(y=x-\ln \left(1+x^{2}\right)\text{;}\)
    7. \(y=x^{\frac{1}{x}}(x>0)\text{.}\)
  5. 证明方程 \(\sin x=x\) 只有一个实根.
  6. 证明方程 \(\mathrm{e}^{x}-x-1=0\) 只有一个实根.
  7. 讨论方程 \(\ln x=a x\) 有几个实根 ( \(a\) 为正常数).
  8. 证明方程 \(a^{x}=b x(a>1)\) 在 \(b>\mathrm{e} \ln a\) 时有两个实根, 在 \(0 \leqslant b \leqslant \mathrm{e} \ln a\) 时没有实根, 在 \(b<0\)时有唯一实根.
  9. 已知函数 \(f(x)\) 在 \([a,+\infty)\) 连续, \(x>a\) 时 \(f^{\prime}(x)>k\text{,}\) 其中 \(k\) 为正常数, 并且 \(f(a)<0\text{,}\) 证明在区间 \(\left(a, a-\frac{f(a)}{k}\right)\) 内函数 \(f(x)\) 有唯一的零点.
  10. 已知 \(f(0)=0, f^{\prime}(x)\) 单调增加, 证明 \(x>0\) 时, \(g(x)=\frac{f(x)}{x}\) 单调增加.
  11. 问常数 \(a\) 取何值时 \(x=\frac{\pi}{3}\) 是函数 \(f(x)=a \sin x+\frac{1}{3} \sin 2 x\) 的极值点, 它是极大值点还是极小值点? 并求此极值.
  12. 已知函数 \(f(x)=\left(x-x_{0}\right)^{n} \varphi(x)\) ( \(n\) 为自然数), \(\varphi(x)\) 在 \(x_{0}\) 点连续. (1) 证明 \(f(x)\) 在 \(x_{0}\)点可导; (2) 若 \(\varphi\left(x_{0}\right) \neq 0\text{,}\) 问 \(x_{0}\) 点是否是 \(f(x)\) 的极值点? 为什么?
  13. 已知 \(f(x)=3 x^{2}+\frac{A}{x^{3}}, A\) 是正常数, 问 \(A\) 至少取什么值才能使对于一切 \(x>0\) 有 \(f(x) \geqslant 20\) ?
  14. 已知函数 \(f(x)\) 在 \(x_{0}\) 点存在 \(n\) 阶非零导数且 \(f^{\prime}\left(x_{0}\right)=f^{\prime \prime}\left(x_{0}\right)=\cdots=f^{(n-1)}\left(x_{0}\right)=0\text{,}\) 证明:若 \(n\) 是奇数, 则 \(x_{0}\) 不是极值点; 若 \(n\) 是偶数, 则当 \(f^{(n)}\left(x_{0}\right)<0\) 时 \(x_{0}\) 为极大值点, 当 \(f^{(n)}\left(x_{0}\right)>0\)时 \(x_{0}\) 为极小值点.
  15. 已知 \(f(x)\) 非负, 常数 \(c>0\text{,}\) 证明函数 \(F(x)=c f^{2}(x)\) 与 \(f(x)\) 有相同的极值点.
  16. 求出下列函数在指定区间上的最大值与最小值 (如果存在):
    1. \(y=x+\cos x,[0,2 \pi]\text{;}\)
    2. \(y=\left|x^{2}-3 x+2\right|,[-10,10]\text{;}\)
    3. \(y=2 \tan x-\tan ^{2} x,\left[0, \frac{\pi}{2}\right)\text{;}\)
    4. \(y=x \mathrm{e}^{-x^{2}},(-\infty,+\infty)\text{.}\)
  17. 求数列 \(x_{n}=\sqrt[n]{n}(n=1,2, \cdots)\) 的最大项.
  18. 证明下列不等式:
    1. \(-2 \leqslant x \leqslant 2\) 时, \(\left|3 x-x^{3}\right| \leqslant 2\text{;}\)
    2. \(0 \leqslant x \leqslant \frac{\pi}{2}\) 时, \(1 \leqslant \sin x+\cos x \leqslant \sqrt{2}\text{;}\)
    3. \(x^{4}-2 x^{3}+2 x+1 \geqslant \frac{5}{16}\text{;}\)
    4. \(x \leqslant 1\) 时, \(4 a x^{3}+3(b-4 a) x^{2}+6(2 a-b) x-2(a-b)<0\text{,}\) 其中 \(a, b\) 是常数, 且 \(0<b<2 a\text{.}\)
  19. 做一个带盖的长方体盒子, 体积为 \(72 \mathrm{~cm}^{3}\text{,}\) 底面的两边之比为 \(1: 2\text{,}\) 问长宽高各多少时 可使盒子的表面积最小.
  20. 半径为 \(R\) 的圆形铁皮截去一个扇形后做成一个圆锥形容器, 问截去的扇形的圆心角多大时做成的圆雉形容器容积最大.
  21. 铁路 \(A B\) 段长 \(100 \mathrm{~km}\text{,}\)工厂 \(C\) 距 \(A 20 \mathrm{~km}, A C\) 垂直于 \(A B\) (见图 4-8). 现在 \(A B\) 上某处 \(D\) 向工厂 \(C\) 修一条公路使原料能从 \(B\) 处运人工厂 \(C\text{,}\) 已知铁路与公路运费之比为 \(3: 5\text{,}\) 为使运费最省 \(D\) 应选在何处?
  22. \(A, B\) 两工厂在河岸同一侧, \(A, B\) 与岸边垂直距离分别为 \(A C=1000 \mathrm{~m}, B D=400 \mathrm{~m}\text{,}\) 而 \(C D=800 \mathrm{~m}\) (见图 4-9). 现在要在 \(C D\) 线上某处 \(E\) 建一水塔供 \(A, B\)两厂用水. 问 \(E\) 应该选在何处,可使所铺设的水管总长最短?
  23. 杠杆支点在一端, 力点在另一端 (见图 4-10). 距支点 \(1 \mathrm{~m}\) 处挂物质量 \(490 \mathrm{~kg}\text{,}\) 杠杆质量均匀分布, 线密度为 \(5 \mathrm{~kg} / \mathrm{m}\text{,}\) 求能使杠杆平衡的最小的力 \(F\) 以及杠杆的长.
PrevTopNext