显然, \(\operatorname{sh} x\) 与 th \(x\) 都是奇函数, \(\operatorname{ch} x\) 是偶函数; 由于 \(\mid\) th \(x \mid<1\text{,}\) 所以 th \(x\) 是有界函数; 在 \((0,+\infty)\) 上 \(\operatorname{sh} x, \operatorname{ch} x, \operatorname{th} x\) 都是单调增加的. 双曲函数有类似于三角函数的一些性质. 容易验证
\begin{equation*}
\begin{gathered}
\operatorname{sh}(x \pm y)=\operatorname{sh} x \operatorname{ch} y \pm \operatorname{ch} x \operatorname{sh} y, \\
\operatorname{ch}(x \pm y)=\operatorname{ch} x \operatorname{ch} y \pm \operatorname{sh} x \operatorname{sh} y, \\
\operatorname{sh} 2 x=2 \operatorname{sh} x \operatorname{ch} x, \\
\operatorname{ch} 2 x=2 \operatorname{ch}^{2} x-1, \\
\operatorname{ch}^{2} x-\operatorname{sh}^{2} x=1 .
\end{gathered}
\end{equation*}
双曲函数 \(y=\operatorname{sh} x, y=\operatorname{ch} x(x \geqslant 0), y=\operatorname{th} x\) 的反函数分别定义为
反双曲正弦 \(y=\operatorname{arsh} x\text{;}\)
反双曲余弦 \(y=\operatorname{arch} x\text{;}\)
反双曲正切 \(y=\operatorname{arth} x\text{.}\)
此外, 反双曲函数也可以从双曲函数的定义中反解出来, 并用对数函数表示. 例如, 由双曲正弦 \(y=\frac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{2}\) 可解得 \(\mathrm{e}^{x}=y \pm \sqrt{y^{2}+1}\text{,}\) 但 \(\mathrm{e}^{x}\) 不取负值, 故舍去 ``\(-\)"号便得
\begin{equation*}
x=\ln \left(y+\sqrt{y^{2}+1}\right),
\end{equation*}
将 \(x\) 表示自变量, \(y\) 表示函数,则反双曲正弦函数为
\begin{equation*}
y=\operatorname{arsh} x=\ln \left(x+\sqrt{x^{2}+1}\right),
\end{equation*}
其定义域为 \((-\infty,+\infty)\text{,}\) 值域为 \((-\infty,+\infty)\text{.}\) 又如, 由双曲余弦 \(y=\frac{\mathrm{e}^{x}+\mathrm{e}^{-x}}{2}\) 可解得 \(\mathrm{e}^{x}=y \pm \sqrt{y^{2}-1}\text{,}\) 即
\begin{equation*}
x=\ln \left(y \pm \sqrt{y^{2}-1}\right)= \pm \ln \left(y+\sqrt{y^{2}-1}\right) .
\end{equation*}
由此可知, 双曲余弦的反函数是双值的. 取其正值的一支作为该函数的主值,于是有
\begin{equation*}
x=\ln \left(y+\sqrt{y^{2}-1}\right),
\end{equation*}
将 \(x\) 表示自变量, \(y\) 表示函数,则反双曲余弦函数为
\begin{equation*}
y=\operatorname{arch} x=\ln \left(x+\sqrt{x^{2}-1}\right),
\end{equation*}
其定义域为 \([1,+\infty)\text{,}\) 值域为 \([0,+\infty)\) 类似地,还可得
\begin{equation*}
y=\operatorname{arth} x=\frac{1}{2} \ln \frac{1+x}{1-x},
\end{equation*}
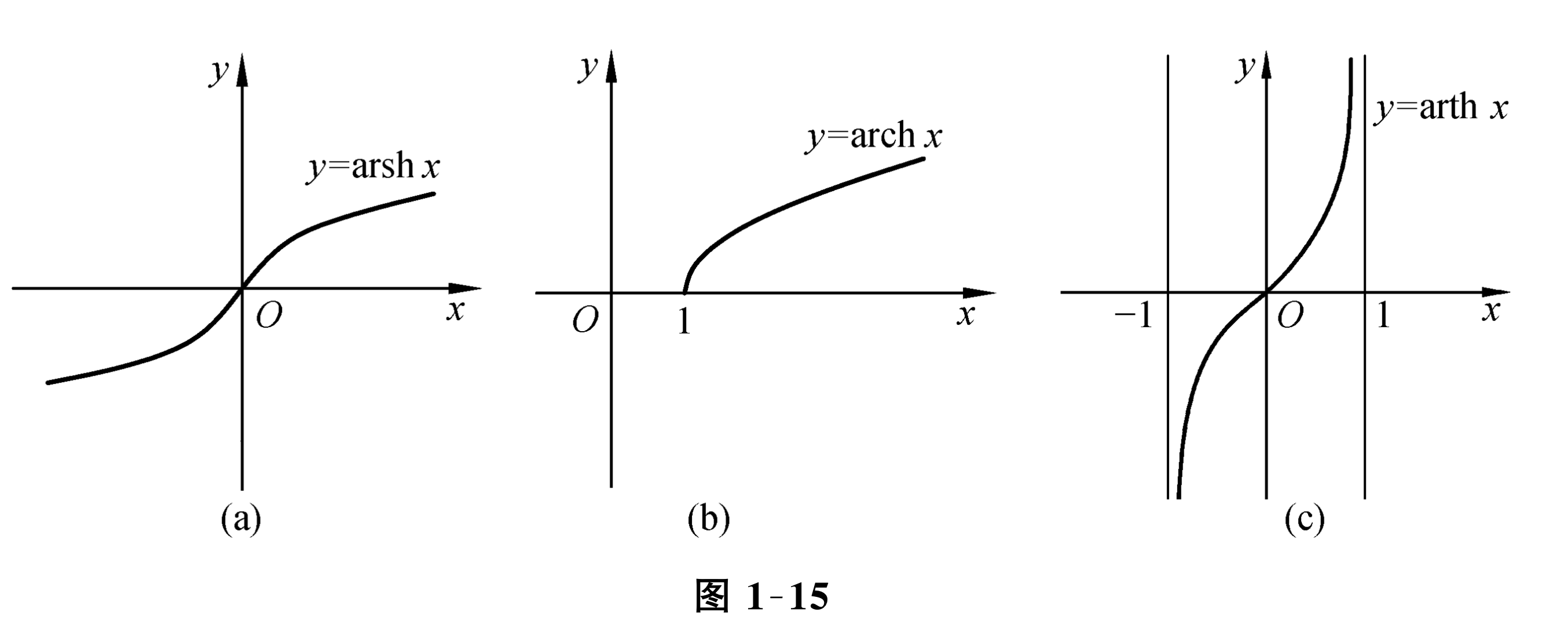
其定义域为 \((-1,1)\text{,}\) 值域为 \([-\infty,+\infty)\text{.}\) 这 3 个反双曲函数的图形分别如图 1-15(a~c) 所示.