Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 2.6 微分

理论研究和实际应用中常常会遇到这样的问题: 当自变量 \(x\) 有微小变化时,求函数 \(y=f(x)\) 的微小改变量 \(\Delta y=f(x+\Delta x)-f(x)\text{.}\) 对于这个问题, 初看起来只需做减法运算即可,然而对于较复杂的函数 \(f(x)\text{,}\) 其差值 \(f(x+\Delta x)-f(x)\) 却是一个很复杂的表达式,不易求出. 我们可以设法将 \(\Delta y\) 表示成 \(\Delta x\) 的线性函数 (即线性化), 从而把复杂问题转化为简单问题. 微分就是实现这种线性化而抽象出来的数学概念.

Subsection 2.6.1 微分的概念

引例 1 一块正方形金属薄片受温度变化的影响, 当其边长由 \(x_{0}\) 变到 \(x_{0}+\) \(\Delta x\) 时, 问此薄片的面积改变了多少? 设此薄片的边长为 \(x\text{,}\) 面积为 \(S\text{,}\) 则 \(S=x^{2}\text{.}\) 薄片受温度变化的影响时面积的改变量, 可以看成是当自变量 \(x\) 自 \(x_{0}\) 取得增量 \(\Delta x\) 时, 函数 \(S=x^{2}\) 相应的增量 \(\Delta S\text{,}\) 即
\begin{equation*} \Delta S=\left(x_{0}+\Delta x\right)^{2}-x_{0}^{2}=2 x_{0} \Delta x+(\Delta x)^{2} . \end{equation*}
从上式可以看出, \(\Delta S\) 分为两部分之和: 一部分 \(2 x_{0} \Delta x\) 是 \(\Delta x\) 的线性函数, 即图 2-19 中带有单斜线的两个矩形面积之和; 另一部分 \((\Delta x)^{2}\) 在图 2-19中是带有交叉斜线的小正方形的面积, 当 \(\Delta x \rightarrow 0\)时, 它是比 \(\Delta x\) 更高阶的无穷小. 由此可见, 如果边长有微小改变, 即 \(|\Delta x|\) 很小时, \((\Delta x)^{2}\) 是 \(|\Delta x|\) 的高阶无穷小,那么相对第一部分 \(2 x_{0} \Delta x\) 可以忽略不计, 从而面积的改变量 \(\Delta S\) 可近似地用第一部分 \(2 x_{0} \Delta x\) 来代替.
引例 2 设 \(y=x^{3}\) 在点 \(x_{0}\) 的改变量为 \(\Delta x\text{,}\) 求函数的改变量 \(\Delta y\text{.}\) 因为 \(\Delta y=\left(x_{0}+\Delta x\right)^{3}-x_{0}^{3}=3 x_{0}^{2} \Delta x+3 x_{0}(\Delta x)^{2}+(\Delta x)^{3}\text{,}\)当 \(|\Delta x|\) 很小时, \(3 x_{0}(\Delta x)^{2}+(\Delta x)^{3}\) 是 \(\Delta x\) 的高阶无穷小, 故 \(\Delta y \approx 3 x_{0}^{2} \Delta x\text{.}\)

Definition 2.6.1.

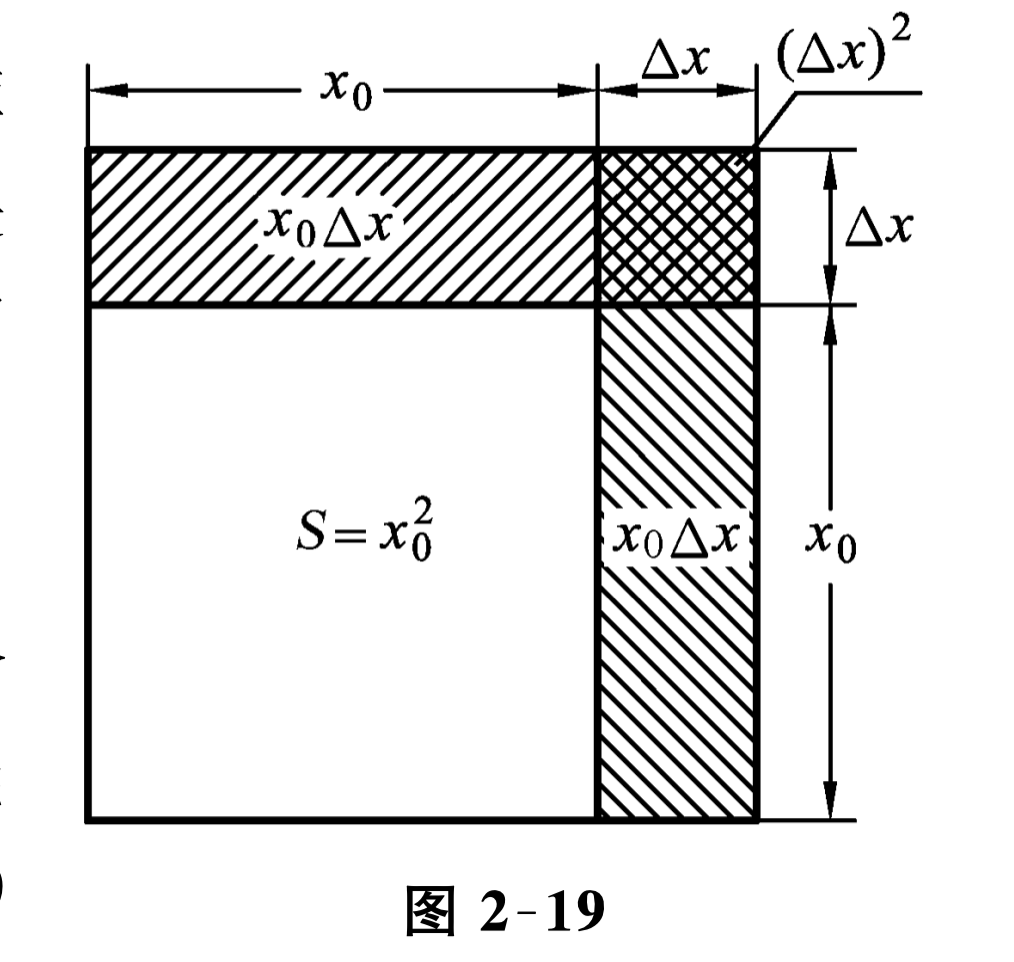
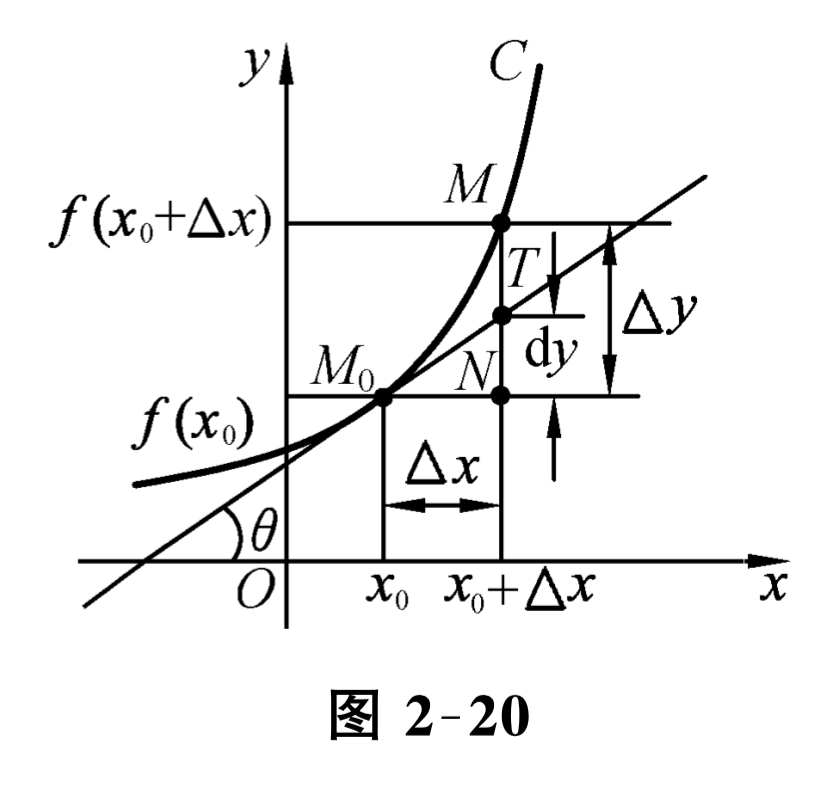
定义 设函数 \(y=f(x)\) 在点 \(x_{0}\) 的某邻域内有定义,若函数 \(y=f(x)\) 在点 \(x_{0}\) 的增量
\begin{equation*} \Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right) \end{equation*}
可以表示成
\begin{equation} \Delta y=A \Delta x+o(\Delta x)\tag{2.6.1} \end{equation}
其中 \(A\) 是与 \(\Delta x\) 无关的常数,则称 \(y=f(x)\) 在点 \(x_{0}\) 可微, \(A \Delta x\) 称为 \(y=f(x)\) 在 \(x_{0}\) 的微分, 记作 \(\mathrm{d} y\text{,}\) 即
\begin{equation} \mathrm{d} y=A \Delta x \text { 或 } \mathrm{d} f(x)=A \Delta x \text {. }\tag{2.6.2} \end{equation}
由定义知, 函数 \(y=f(x)\) 在点 \(x_{0}\) 处的微分 \(A \Delta x\) 是 \(\Delta x\) 的一次函数, 是相应于自变量增量 \(\Delta x\) 的函数 \(y=f(x)\) 增量 \(\Delta y\) 的线性主部.

Subsection 2.6.2 可微的充分必要条件

满足何种条件, \(f(x)\) 才是可微的呢? 当 \(f(x)\) 在 \(x_{0}\) 可微时, 常数 \(A\) 的值是多少? 在引例 1 中 \(S=x^{2}\) 在 \(x_{0}\) 处可微,其中 \(A=S^{\prime}\left(x_{0}\right)=2 x_{0}\text{,}\) 在引例 2 中 \(y=x^{3}\) 在 \(x_{0}\) 处可微, 其中 \(A=y^{\prime}\left(x_{0}\right)=3 x_{0}^{2}\text{.}\) 一般地, 有以下定理.

Proof.

证 必要性. 因为函数 \(f(x)\) 在点 \(x_{0}\) 可微,即
\begin{equation*} \Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)=A \cdot \Delta x+o(\Delta x), \end{equation*}
两边除以 \(\Delta x\text{,}\) 并令 \(\Delta x \rightarrow 0\text{,}\) 则有
\begin{equation*} \lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=A \text {. } \end{equation*}
由于 \(f(x)\) 在点 \(x_{0}\) 处可导,所以 \(A=f^{\prime}\left(x_{0}\right)\text{,}\)故有
\begin{equation*} \mathrm{d} y=f^{\prime}\left(x_{0}\right) \Delta x \end{equation*}
充分性. 因为 \(f(x)\) 在 \(x_{0}\) 点可导,由Subsection 2.1.5式 (2.1.12) 可知,
\begin{equation*} \Delta y=f^{\prime}\left(x_{0}\right) \Delta x+\alpha \Delta x, \end{equation*}
其中 \(\lim\limits_{\Delta x \rightarrow 0} \alpha=0\text{,}\) 所以 \(\lim\limits_{\Delta x \rightarrow 0} \frac{\alpha \Delta x}{\Delta x}=0\text{,}\) 即 \(\alpha \Delta x=o(\Delta x)\text{,}\) 又 \(f^{\prime}\left(x_{0}\right)\) 与 \(\Delta x\) 无关, 由微分的定义知, \(y=f(x)\) 在 \(x_{0}\) 点可微, 且有
\begin{equation*} \mathrm{d} y=f^{\prime}\left(x_{0}\right) \Delta x \text {. } \end{equation*}
定理证毕.
本定理表明,对于一元函数, 可微与可导是等价的,求导数和求微分都称为微分法. 若函数 \(f(x)\) 在区间 \((a, b)\) 内每点都可微, 则称函数 \(f(x)\) 在 \((a, b)\) 内可微, 此时记为
\begin{equation} \mathrm{d} y=f^{\prime}(x) \Delta x\tag{2.6.3} \end{equation}
特别地, 当 \(y=f(x)=x\) 时, \(f^{\prime}(x)=1\text{,}\) 则有
\begin{equation*} \mathrm{d} y=\mathrm{d} x=1 \cdot \Delta x, \Delta x=\mathrm{d} x, \end{equation*}
所以函数 \(f(x)\) 的微分可以写为
\begin{equation} \mathrm{d} y=f^{\prime}(x) \mathrm{d} x, \tag{2.6.4} \end{equation}
于是有
\begin{equation*} \frac{\mathrm{d} y}{\mathrm{~d} x}=f^{\prime}(x) . \end{equation*}
可见函数的导数可以看成函数的微分与自变量的微分之商, 因此,导数又称为“微商”. 前面把 \(\frac{\mathrm{d} y}{\mathrm{~d} x}\) 看成一个整体记号, 有了微分概念后, 就可把它看成一个比式. 注意 导数与微分虽然有密切的联系,但它们是有明显区别的: 导数是函数在一点处的变化率,而微分是函数在一点处由自变量增量所引起的函数增量的主要部分; 导数的值只与点 \(x\) 有关,而微分的值与点 \(x\) 和自变量增量 \(\Delta x\) 都有关,而且 \(|\Delta x|\) 不一定很小.

Subsection 2.6.3 微分的几何意义

在曲线 \(y=f(x)\) 上取横坐标为 \(x_{0}\) 的一点 \(M_{0}\text{,}\) 过 \(M_{0}\) 作曲线的切线 \(M_{0} T\text{,}\) 它的倾角为 \(\theta\text{,}\) 给 \(x_{0}\) 以增量 \(\Delta x\text{,}\) 对应于坐标 \(x_{0}+\Delta x\text{,}\) 曲线与切线上分别有点 \(M, T\) ( 见 图 2-20).
由图 2-20 可以看出
\begin{equation*} \begin{gathered} N M=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)=\Delta y, \\ N T=\tan \theta \cdot \Delta x=f^{\prime}\left(x_{0}\right) \Delta x=\mathrm{d} y, \\ T M=\Delta y-\mathrm{d} y=\alpha \Delta x=o(\Delta x) . \end{gathered} \end{equation*}
由此可见,函数 \(y=f(x)\) 在点 \(x_{0}\) 处的微分 \(\mathrm{d} y\) 表示曲线在点 \(M_{0}\) 处的切线当 \(x_{0}\) 有增量 \(\Delta x\) 时纵坐标的增量. 当 \(|\Delta x| \ll 1\) 时,若用微分 \(\mathrm{d} y=f^{\prime}\left(x_{0}\right) \Delta x\) 代替增量 \(\Delta y\text{,}\) 可得
\begin{equation} f\left(x_{0}+\Delta x\right) \approx f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right) \Delta x .\tag{2.6.5} \end{equation}
由图 2-20 可知, 就是用 \(N T\) 去代替 \(N M\text{,}\) 两者之差为 \(T M\text{,}\) 所以式(2.6.5)表明在点 \(x_{0}\) 的附近可用切线近似代替原来的曲线,即用一个线性函数去近似代替原来的函数. 简单地说, 就是用直线的增量去代替曲线的增量, 即 “以直代曲”, 使计算得以简化. 若记 \(x_{0}+\Delta x=x\text{,}\) 即 \(\Delta x=x-x_{0}\text{,}\) 则有
\begin{equation} f(x) \approx f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right),\tag{2.6.6} \end{equation}
特别地, 当 \(x_{0}=0\) 时, \(\Delta x=x-x_{0}=x\text{,}\) 由(2.6.6)有
\begin{equation} f(x) \approx f(0)+f^{\prime}(0) x .\tag{2.6.7} \end{equation}

Example 2.6.3.

例 1 设函数 \(y=x^{3}\text{,}\) 求:
  1. 函数的微分;
  2. 函数在 \(x=2\) 处的微分;
  3. 函数在 \(x=2\) 处当 \(\Delta x=0.01\) 时的增量 \(\Delta y\text{,}\)微分 \(\mathrm{d} y\) 以及 \(\Delta y-\mathrm{d} y\text{.}\)
Solution.
解 (1) \(\mathrm{d} y=y^{\prime} \mathrm{d} x=3 x^{2} \mathrm{~d} x\text{;}\)
  1. \(\left.\mathrm{d} y\right|_{x=2}=\left.3 x^{2}\right|_{x=2} \mathrm{~d} x=12 \mathrm{~d} x\text{;}\)
  2. \(\left.\mathrm{d} y\right|_{\substack{x=2 \\ \Delta x=0.01}}=\left.3 x^{2} \mathrm{~d} x\right|_{\substack{x=2 \\ \Delta x=0.01}}=12 \times 0.01=0.12\text{,}\)
\begin{equation*} \begin{gathered} \Delta y=(2+0.01)^{3}-2^{3}=0.120601, \\ \Delta y-\mathrm{d} y=0.000601, \end{gathered} \end{equation*}
可见用 \(\mathrm{d} y\) 近似代替 \(\Delta y\) 其误差绝对值小于 \(10^{-3}\text{.}\)

Subsection 2.6.4 微分法则

因为 \(\mathrm{d} y=f^{\prime}(x) \mathrm{d} x\text{,}\) 所以求函数的微分时, 只需求出函数的导数再乘以 \(\mathrm{d} x\) 即可. 因此, 每一个导数公式都对应着一个微分公式, 例如, \(y=\tan x\) 的导数为 \(y^{\prime}=\) \(\sec ^{2} x\text{,}\) 微分为 \(\mathrm{d} y=\sec ^{2} x \mathrm{~d} x\text{.}\) 类似地, 由导数的四则运算法则可得微分的四则运算法则.

Proof.

证明由读者作为练习自己完成.
由导数公式容易得到相应的微分公式, 为便于查阅与对照, 将一些初等函数的导数与微分公式列于下表. *** Miss table

Example 2.6.5.

例 2 设 \(y=\mathrm{e}^{x} \sin x\text{,}\) 求 \(\mathrm{d} y\text{.}\)
Solution.
解 令 \(u=\mathrm{e}^{x}, v=\sin x\text{,}\) 则
\begin{equation*} \begin{gathered} \mathrm{d} y=\mathrm{d}(u \cdot v)=u \mathrm{~d} v+v \mathrm{~d} u=\mathrm{e}^{x} \mathrm{~d} \sin x+\sin x \mathrm{de}^{x} \\ =\mathrm{e}^{x} \cos x \mathrm{~d} x+\mathrm{e}^{x} \sin x \mathrm{~d} x=\mathrm{e}^{x}(\sin x+\cos x) \mathrm{d} x, \end{gathered} \end{equation*}
或
\begin{equation*} y^{\prime}=\left(\mathrm{e}^{x} \sin x\right)^{\prime}=\mathrm{e}^{x} \sin x+\mathrm{e}^{x} \cos x=\mathrm{e}^{x}(\sin x+\cos x), \end{equation*}
故
\begin{equation*} \mathrm{d} y=y^{\prime} \mathrm{d} x=\mathrm{e}^{x}(\sin x+\cos x) \mathrm{d} x . \end{equation*}
现在讨论复合函数的微分. 设 \(y=f(u), u=\varphi(x)\) 都可导,则复合函数 \(y=f[\varphi(x)]\) 的导数为
\begin{equation*} \frac{\mathrm{d} y}{\mathrm{~d} x}=f^{\prime}[\varphi(x)] \varphi^{\prime}(x), \end{equation*}
其微分为
\begin{equation*} \mathrm{d} y=f^{\prime}[\varphi(x)] \varphi^{\prime}(x) \mathrm{d} x, \end{equation*}
注意到
\begin{equation*} f^{\prime}[\varphi(x)]=f^{\prime}(u), \mathrm{d} u=\varphi^{\prime}(x) \mathrm{d} x, \end{equation*}
所以
\begin{equation*} \mathrm{d} y=f^{\prime}(u) \mathrm{d} u \text {. } \end{equation*}
由此可见,对 \(y=f(u)\) 求微分时,无论 \(u\) 是自变量还是另一变量的可微函数,其微分形式 \(\mathrm{d} y=f^{\prime}(u) \mathrm{d} u\) 保持不变, 这个重要性质称为微分形式不变性. 微分形式不变性在理论和计算上都有重要意义.

Example 2.6.6.

例 3 设 \(y=\ln \cos x^{2}\text{,}\) 求 \(\mathrm{d} y\text{.}\)
Solution.
解 \(\mathrm{d} y=\frac{1}{\cos x^{2}} \mathrm{~d}\left(\cos x^{2}\right)=\frac{1}{\cos x^{2}}\left(-\sin x^{2}\right) \mathrm{d}\left(x^{2}\right)\)
\begin{equation*} =-\tan x^{2} \cdot 2 x \mathrm{~d} x=-2 x \tan x^{2} \mathrm{~d} x . \end{equation*}
利用微分形式不变性也可以求出相应的导数.

Example 2.6.7.

例 4 设方程 \(\sin (x y)+\ln \left(x+y^{2}\right)=1\) 确定函数 \(y=y(x)\text{,}\) 利用微分形式不变性, 求 \(y^{\prime}\text{.}\)
Solution.
解 方程两边求微分, 得
\begin{equation*} \begin{gathered} \mathrm{d}(\sin x y)+\mathrm{d}\left[\ln \left(x+y^{2}\right)\right]=0, \\ \cos (x y) \mathrm{d}(x y)+\frac{1}{x+y^{2}} \mathrm{~d}\left(x+y^{2}\right)=0, \\ \cos (x y)(x \mathrm{~d} y+y \mathrm{~d} x)+\frac{1}{x+y^{2}}(\mathrm{~d} x+2 y \mathrm{~d} y)=0, \\ {\left[x \cos (x y)+\frac{2 y}{x+y^{2}}\right] \mathrm{d} y+\left[y \cos (x y)+\frac{1}{x+y^{2}}\right] \mathrm{d} x=0,} \end{gathered} \end{equation*}
\begin{equation*} \mathrm{d} y=-\frac{y \cos (x y)+\frac{1}{x+y^{2}}}{x \cos (x y)+\frac{2 y}{x+y^{2}}} \mathrm{~d} x \end{equation*}
从而
\begin{equation*} y^{\prime}=-\frac{y \cos (x y)+\frac{1}{x+y^{2}}}{x \cos (x y)+\frac{2 y}{x+y^{2}}}=-\frac{\left(x+y^{2}\right) y \cos (x y)+1}{\left(x+y^{2}\right) x \cos (x y)+2 y} \end{equation*}

Subsection 2.6.5 微分的应用举例

Subsubsection 2.6.5.1 函数的线性化

前面已经指出, 若函数 \(y=f(x)\) 在 \(x_{0}\) 处可微,则当 \(|\Delta x|=\left|x-x_{0}\right|\) 很小时, 可以用微分 \(\mathrm{d} y\) 近似代替增量 \(\Delta y\text{.}\) 若记(2.6.6) 右端的线性函数为 \(p_{1}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\text{,}\) 则其图形就是曲线 \(y=f(x)\) 过点 \(\left(x_{0}, f\left(x_{0}\right)\right)\) 的切线. (2.6.6)表明: 当 \(|\Delta x|=\left|x-x_{0}\right|\) 很小时,线性函数 \(p_{1}(x)\) 给出了函数 \(f(x)\) 很好的近似. 当 \(f\left(x_{0}\right), f^{\prime}\left(x_{0}\right)\) 容易计算时,便可以利用 \(p_{1}(x)\) 近似计算 \(f(x)\text{.}\) 若函数 \(f(x)\) 在 \(x_{0}\) 处可微,则称线性函数 \(p_{1}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\) 为 \(f(x)\) 在点 \(x_{0}\) 处的线性化,并称近似式 \(f(x) \approx p_{1}(x)\) 为 \(f(x)\) 在点 \(x_{0}\) 处的标准线性近似。
Example 2.6.8.
例 5 为使摆长 \(l=20 \mathrm{~cm}\) 单摆振动周期增大 \(0.05 \mathrm{~s}\text{,}\) 其摆长应调整为多少?
Solution.
解 由物理学知, 单摆振动的周期 \(T\) 与摆长 \(l\) 的函数关系为
\begin{equation*} T=2 \pi \sqrt{\frac{l}{g}}, \end{equation*}
其中 \(T\) 的单位为 \(\mathrm{s}, l\) 的单位为 \(\mathrm{cm}, g=981 \mathrm{~cm} / \mathrm{s}^{2}\text{.}\) 因为 \(T=T(l)\) 是严格单调增加函数, 故其反函数 \(l=l(T)\) 存在, \(l=\frac{T^{2} g}{4 \pi^{2}}\text{,}\) 且
\begin{equation*} l_{T}^{\prime}=\frac{T g}{2 \pi^{2}}=\frac{\sqrt{g l}}{\pi} . \end{equation*}
设摆长 \(l=20 \mathrm{~cm}\) 时相应的周期为 \(T, \Delta T=0.05 \mathrm{~s}\text{,}\) 则
\begin{equation*} \begin{aligned} l(T+\Delta T) & \approx l(T)+l^{\prime}(T) \Delta T=l(T)+\frac{\sqrt{g l}}{\pi} \Delta T \\ & =20+\frac{\sqrt{981 \times 20} \times 0.05}{3.142} \approx 20+2.23=22.23 \mathrm{~cm}, \end{aligned} \end{equation*}
即为使振动周期增加 \(0.05 \mathrm{~s}\text{,}\) 摆长应调整为 \(22.23 \mathrm{~cm}\text{.}\)
Example 2.6.9.
例 6 半径为 \(1 \mathrm{~m}\) 的球, 当其半径增加 \(1 \mathrm{~cm}\) 时, 估计球体积的增量.
Solution.
解 球体积 \(V=\frac{4}{3} \pi r^{3}\text{,}\) 所以
\begin{equation*} \Delta V \approx \mathrm{d} V=4 \pi r^{2} \Delta r . \end{equation*}
已知 \(r=1 \mathrm{~m}, \Delta r=0.01 \mathrm{~m}\text{,}\) 代人上式, 得
\begin{equation*} \Delta V \approx 4 \pi \times 1^{2} \times 0.01 \approx 0.13 \mathrm{~m}^{3} . \end{equation*}
Example 2.6.10.
例 7 计算 \(\sqrt{325}\) 的近似值.
Solution.
解 因为 \(\sqrt{325}=\sqrt{324+1}=18 \sqrt{1+\frac{1}{324}}\text{.}\) 令 \(f(x)=\sqrt{1+x}\text{,}\) 则 \(f(0)=1, x=\frac{1}{324}\text{.}\)
\begin{equation*} \begin{gathered} f(x) \approx f(0)+f^{\prime}(0) x=1+\left.\frac{1}{2 \sqrt{1+x}}\right|_{x=0} \cdot x=1+\frac{1}{2} x, \\ \sqrt{1+\frac{1}{324}} \approx 1+\frac{1}{2} \times \frac{1}{324}=\frac{649}{648}, \end{gathered} \end{equation*}
所以
\begin{equation*} \sqrt{325} \approx 18 \times \frac{649}{648} \approx 18.03 \end{equation*}
将关系(2.6.7) 用于具体函数, 可以得到一些常用的近似计算公式 (假设 \(|x|\)较小):
\begin{equation*} \begin{array}{ll} \sin x \approx x ; & \arcsin x \approx x ; \\ \tan x \approx x ; & \arctan x \approx x ; \\ \mathrm{e}^{x} \approx 1+x ; & \ln (1+x) \approx x ; \\ \sqrt[n]{1+x} \approx 1+\frac{1}{n} x . & \end{array} \end{equation*}
上述近似等式的证明由读者自己完成.
Example 2.6.11.
例 8 求 \(\sin 1^{\circ}\) 的值.
Solution.
解 \(1^{\circ}=\frac{\pi}{180} \mathrm{rad}\text{,}\) 由 \(\sin x \approx x\text{,}\) 有
\begin{equation*} \sin 1^{\circ}=\sin \frac{\pi}{180} \approx \frac{\pi}{180} \approx 0.0175 . \end{equation*}
Example 2.6.12.
例 9 (质能转换) 牛顿第二运动定律 \(F=\frac{\mathrm{d}}{\mathrm{d} t}(m v)=m \frac{\mathrm{d} v}{\mathrm{~d} t}=m a\) 的这种陈述是假定质量为常数 (即固定不变), 但严格来说这并不正确, 因为物体的质量随其速度的增长而增长. 在爱因斯坦修正后的公式中, 质量为 \(m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\text{,}\) 其中“静止质量 \(m_{0}\) ”表示没有运动时物体的质量, 而 \(c\) 是光速, 大约为 \(300000 \mathrm{~km} / \mathrm{s}\text{.}\) 试利用近似式
\begin{equation*} \frac{1}{\sqrt{1-x^{2}}} \approx 1+\frac{1}{2} x^{2} \end{equation*}
估计因考虑速度 \(v\) 后质量的增长量 \(\Delta m\text{.}\)
Solution.
解 当 \(v\) 和 \(c\) 相比很小时, \(\frac{v^{2}}{c^{2}}\) 接近于零, 从而可安全地利用 \(\frac{1}{\sqrt{1-v^{2} / c^{2}}} \approx\) \(1+\frac{1}{2}\left(\frac{v^{2}}{c^{2}}\right)\text{,}\) 从而有
\begin{equation*} \begin{gathered} m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \approx m_{0}\left[1+\frac{1}{2}\left(\frac{v^{2}}{c^{2}}\right)\right]=m_{0}+\frac{1}{2} m_{0} v^{2}\left(\frac{1}{c^{2}}\right), \\ m \approx m_{0}+\frac{1}{2} m_{0} v^{2}\left(\frac{1}{c^{2}}\right) . \end{gathered} \end{equation*}
即 上式表示考虑速度 \(v\) 后所产生的质量的增长量. 在牛顿物理学中, \(\frac{1}{2} m_{0} v^{2}\) 是物体的动能 \(\left(E_{\mathrm{k}}\right)\text{,}\) 若将 \(m \approx m_{0}+\frac{1}{2} m_{0} v^{2}\left(\frac{1}{c^{2}}\right)\) 改写成 \(\left(m-m_{0}\right) c^{2} \approx \frac{1}{2} m_{0} v^{2}\) 的形式,那么就得到 或
\begin{equation*} \begin{gathered} \left(m-m_{0}\right) c^{2} \approx \frac{1}{2} m_{0} v^{2}=\Delta E_{\mathrm{k}} \\ (\Delta m) c^{2} \approx \Delta E_{\mathrm{k}} . \end{gathered} \end{equation*}
换言之, 从速度 0 到速度 \(v\) 的动能的变化 \(\Delta E_{\mathrm{k}}\) 近似等于 \((\Delta m) c^{2}\text{.}\) 因为 \(c=3 \times\) \(10^{8} \mathrm{~m} / \mathrm{s}\text{,}\) 所以 \(\Delta E_{\mathrm{k}} \approx 9 \times 10^{16} \Delta m(\mathrm{~J})\text{.}\) 由此已知,小的质量变化可以创造出大的能量变化.

Subsubsection 2.6.5.2 误差估计

微分可以用来解决测量问题中的误差估计问题, 在测量问题中,有些量的大小可以直接测量得到, 这些数据称为直接测量数据; 有些量是根据公式计算得到的, 这样得到的数据称为间接测量数据. 例如, 钢珠的直径 \(D\) 可用游标卡尺直接测得 (它为直接测量数据), 而其体积由公式 \(V=\frac{\pi}{6} D^{3}\) 算出 (它为间接测量数据).
由于测量仪器的精度, 测量的条件和测量方法等诸多因素的影响, 直接测量的数据会有误差, 因而根据这些数据计算出来的间接测量数据也会有误差, 称为间接测量误差.
设直接测量数据为 \(a\text{,}\) 精确值为 \(A\text{,}\) 称 \(|A-a|\) 为 \(a\) 的绝对误差, 而比值 \(\frac{|A-a|}{|a|}\)称为 \(a\) 的相对误差.
实际上, 由于精确值未知, 故 \(|A-a|\) 也往往无法知道, 只能根据情况估计出 \(|A-a|\) 的上界,这个上界称为 \(a\) 的绝对误差限或绝对误差, 记作 \(\delta_{A}\text{,}\) 即
\begin{equation*} |A-a| \leqslant \delta_{A} . \end{equation*}
\(\frac{\delta_{A}}{|a|}\) 称为 \(a\) 的相对误差限或相对误差.
设 \(x\) 由直接测量得到, \(y\) 由公式 \(y=f(x)\) 计算而得, 现求由 \(x\) 的误差引起 \(y\) 的误差. 如果 \(x\) 的绝对误差为 \(\delta_{x}\text{,}\) 即
\begin{equation*} |\Delta x| \leqslant \delta_{x}, \end{equation*}
那么当 \(y^{\prime} \neq 0\) 时,
\begin{equation*} |\Delta y| \approx|\mathrm{d} y|=\left|f^{\prime}(x)\right||\Delta x| \leqslant\left|f^{\prime}(x)\right| \delta_{x}, \end{equation*}
即 \(y\) 的绝对误差为
\begin{equation*} \delta_{y}=\left|f^{\prime}(x)\right| \delta_{x}, \end{equation*}
所以 \(y\) 的相对误差为
\begin{equation*} \frac{\delta_{y}}{|y|}=\frac{\left|f^{\prime}(x)\right|}{|f(x)|} \delta_{x} \end{equation*}
Example 2.6.13.
例 10 设测得圆盘的直径 \(x=5.2 \mathrm{~cm}\text{,}\) 其绝对误差为 \(\delta_{x}=0.05 \mathrm{~cm}\text{,}\) 试估计圆盘面积的绝对误差与相对误差.
Solution.
解 由面积公式 \(y=\frac{\pi}{4} x^{2}\) 可知, 面积的绝对误差为
\begin{equation*} \delta_{y}=\left|y^{\prime}\right| \cdot \delta_{x}=\frac{\pi}{2} x \delta_{x}=\frac{\pi}{2} \times 5.2 \times 0.05 \approx 0.41 \mathrm{~cm}^{2} \end{equation*}
面积的相对误差为
\begin{equation*} \frac{\delta_{y}}{|y|}=\frac{\frac{\pi}{2} x \delta_{x}}{\frac{\pi}{4} x^{2}}=2 \frac{\delta_{x}}{|x|}=2 \times \frac{0.05}{5.2} \approx 0.0192 \approx 2 \% \text {. } \end{equation*}
Example 2.6.14.
例11 (打开受阻塞的动脉) 19 世纪 30 年代后期, 法国生理学家普瓦泽伊发现了必须扩张部分受阻塞的动脉半径与恢复正常的血液流动之间的关系的规律.他的研究公式 \(V=k r^{4}\) 表明, 以固定的压力在单位时间内流过细管的体积 \(V\) 等于一个常数乘以管半径 \(r\) 的四次幕. 试求当半径 \(r\) 增加 \(10 \%\) 对 \(V\) 的影响有多大?
Solution.
解 \(r\) 的微分和 \(V\) 的微分之间的关系由方程
\begin{equation*} \mathrm{d} V=\frac{\mathrm{d} V}{\mathrm{~d} r} \mathrm{~d} r=4 k r^{3} \mathrm{~d} r \end{equation*}
表示, \(V\) 的相对变化为
\begin{equation*} \frac{\mathrm{d} V}{V}=\frac{4 k r^{3} \mathrm{~d} r}{k r^{4}}=4 \frac{\mathrm{d} r}{r} \end{equation*}
\(V\) 的相对变化为 \(r\) 的相对变化的 4 倍,所以 \(10 \%\) 的 \(r\) 增加将产生 \(40 \%\) 的流量增长.

Subsubsection 2.6.5.3 边际成本

工程师用速度和加速度等术语描述运动的函数的导数. 对于变化率和导数, 经济学家称其为边际. 假设 \(c(x)\) 表示每周生产 \(x\) 吨钢所需的成本,每周生产 \((x+h)\) 吨钢的成本就会高一些, 成本的差价除以 \(h\) 就是生产附加的 \(h\) 吨钢的平均成本, 即
\begin{equation*} \frac{c(x+h)-c(x)}{h}=\text { 每多生产 } h \text { 吨钢的平均成本. } \end{equation*}
在当前每周生产 \(x\) 吨的情形下,称当 \(h \rightarrow 0\) 时上式比值的极限为每周生产更多钢的边际成本 (见图 2-21), 简称为生产的边际成本, 即
\begin{equation*} \frac{\mathrm{d} c}{\mathrm{~d} x}=\lim\limits_{h \rightarrow 0} \frac{c(x+h)-c(x)}{h}=\text { 生产的边际成本. } \end{equation*}
类似的方法可以定义边际收人. 有时将生产的边际成本不严格地定义为多生产一个单位产品的附加成本, 即
\begin{equation*} \frac{\Delta c}{\Delta x}=\frac{c(x+1)-c(x)}{1} \end{equation*}
它近似为 \(\frac{\mathrm{d} c}{\mathrm{~d} x}\) 在 \(x\) 的值. 如果 \(c(x)\) 曲线在 \(x\) 附近的斜率变化不大, 这种近似是可以接受的, 那么差商接近于极限 \(\frac{\mathrm{d} c}{\mathrm{~d} x}\text{.}\) 如果 \(\Delta x=1, \frac{\mathrm{d} c}{\mathrm{~d} x}\) 就是切线所表示的成本增长 (见图 2-22). 当 \(x \gg \Delta x\) 时,该近似值的符合程度较佳.
Example 2.6.15.
例 12 假设在生产 8～30 台散热器的情况下,生产 \(x\) 台散热器的成本为
\begin{equation*} c(x)=x^{3}-6 x^{2}+15 x(\text { 元 }), \end{equation*}
而售出 \(x\) 台散热器的收人为
\begin{equation*} r(x)=x^{3}-3 x^{2}+12 x(\text { 元 }) . \end{equation*}
工厂目前每天生产 10 台散热器, 则每天多生产 1 台散热器的附加成本为多少? 每天售出 11 台散热器又会增加多少收人?
Solution.
解 工厂在每天生产 10 台散热器的情况下, 每天多生产 1 台的成本大约为 \(c^{\prime}(10)\) :
\begin{equation*} c^{\prime}(x)=\frac{\mathrm{d}}{\mathrm{d} x}\left(x^{3}-6 x^{2}+15 x\right)=3 x^{2}-12 x+15, \end{equation*}
\begin{equation*} c^{\prime}(10)=3 \times(10)^{2}-12 \times 10+15=195, \end{equation*}
即附加成本约为 195 元. 边际收人为
\begin{equation*} r^{\prime}(x)=\frac{\mathrm{d}}{\mathrm{d} x}\left(x^{3}-3 x^{2}+12 x\right)=3 x^{2}-6 x+12, \end{equation*}
边际收人约为多卖出 1 台散热器增加的收人. 如果目前每天售出 10 台, 那么每天销售量增加到 11 台时, 预期可以增加的收人约为
\begin{equation*} r^{\prime}(10)=3 \times(10)^{2}-6 \times 10+12=252 \text { (元). } \end{equation*}

Subsubsection 2.6.5.4 需求弹性

需求对价格变化的敏感度与产品有关. 例如, 灯泡价格的变化可能不会影响其需求量, 因为不论灯泡的价格如何, 人们都需要灯泡. 然而, 某特定款式的汽车的价格变化可能对需求量有重大的影响,因为人们可以转向其他款式. 因此, 人们需要一种方法衡量需求对价格变化的敏感度, 该衡量方法应该对灯泡、汽车等多样化的产品都行之有效. 由于这两个产品的价格差别太大, 讨论价格的绝对变化是没有意义的: 灯泡的价格变化 10 元是一个很大的变化,但汽车的价格变化 10 元则不是. 这里改为讨论价格的变化百分比. 例如,价格 \(1 \%\) 的变化是如何影响产品需求量的? 设 \(\Delta P\) 是某产品价格 \(P\) 的变化量, \(\Delta Q\) 是相应需求量 \(Q\) 的变化量,则价格的变化百分比为 \(\frac{\Delta P}{P}\text{,}\) 需求量的变化百分比为 \(\frac{\Delta Q}{Q}\text{.}\) 注意到 \(\Delta P\) 和 \(\Delta Q\) 通常有相反的符号 (因为提高价格将降低需求量). 价格变化对需求量的影响就由比率的绝对值
\begin{equation*} \left|\frac{\text { 需求的变化百分比 }}{\text { 价格的变化百分比 }}\right|=\left|\frac{\frac{\Delta Q}{Q}}{\frac{\Delta P}{P}}\right|=\left|\frac{\Delta Q}{Q} \cdot \frac{P}{\Delta P}\right|=\left|\frac{P}{Q} \cdot \frac{\Delta Q}{\Delta P}\right| \end{equation*}
衡量. 当 \(P\) 变化较小时, 可用导数 \(\frac{\mathrm{d} Q}{\mathrm{~d} P}\) 代替 \(\frac{\Delta Q}{\Delta P}\text{.}\) 产品需求弹性 \(E\) 由 \(E \approx\left|\frac{\frac{\Delta Q}{Q}}{\frac{\Delta P}{P}}\right|\) 近似或 \(E=\left|\frac{P}{Q} \cdot \frac{\mathrm{d} Q}{\mathrm{~d} P}\right|\) 精确给出. 商品价格提高 \(1 \%\text{,}\) 将导致商品需求量大约下降 \(E \%\text{.}\)对价格的小变化量 \(\Delta P\text{,}\) 有 \(\frac{\Delta Q}{Q} \approx-E \frac{\Delta P}{P}\text{.}\) 如果 \(E>1\text{,}\) 价格上涨 \(1 \%\) 导致需求量下降超过 \(1 \%\text{,}\) 那么此时称需求是弹性的; 如果 \(0 \leqslant E<1\text{,}\) 价格上涨 \(1 \%\) 导致需求量下降小于 \(1 \%\text{,}\) 那么此时称需求是非弹性的.
Example 2.6.16.
例 13 某产品的需求曲线为 \(Q=1000-2 P^{2}\text{,}\) 其中 \(P\) 是价格. 求 \(P=10\) 时的 需求弹性.
Solution.
解 由已知得 \(\frac{\mathrm{d} Q}{\mathrm{~d} P}=-4 P\text{.}\) 当价格 \(P=10\) 时, 有 \(\frac{\mathrm{d} Q}{\mathrm{~d} P}=-4 \times 10=-40\text{,}\) 需求量为 \(Q=1000-2 \times 10^{2}=\) 800. 在这个价格水平下, 需求弹性为
\begin{equation*} E=\left|\frac{P}{Q} \cdot \frac{\mathrm{d} Q}{\mathrm{~d} P}\right|=\left|\frac{10}{800} \times(-40)\right|=0.5 . \end{equation*}
因此在价格 \(P=10\) 时,需求是非弹性的: 价格上涨 \(1 \%\) 导致需求量大约降低 \(0.5 \%\text{.}\) 在价格 \(P=15\) 时, 有 \(\frac{\mathrm{d} Q}{\mathrm{~d} P}=-4 \times 15=-60\text{,}\) 需求量为 \(Q=1000-2 \times 15^{2}=550\text{.}\) 需求弹性为
\begin{equation*} E=\left|\frac{P}{Q} \cdot \frac{\mathrm{d} Q}{\mathrm{~d} P}\right|=\left|\frac{15}{550} \times(-60)\right|=1.64 . \end{equation*}
即价格上涨 \(1 \%\) 导致需求量大约降低 \(1.64 \%\text{,}\) 所以需求是弹性的.

Subsection 2.6.6 本节知识图谱

Figure 2.6.17. 知识图谱

Subsection 2.6.7 习题 2-6

  1. 求函数 \(y=x^{2}+1\text{,}\) 当 \(x=3\) 时 \(\Delta x\) 分别为 \(0.1,0.01,-0.2\) 时 \(\Delta y\) 及 \(\mathrm{d} y\) 之值.
  2. 求下列函数的微分 \(\mathrm{d} y\) :
    1. \(y=x \ln x\text{;}\)
    2. \(y=\frac{a}{x}+\arctan \frac{a}{x}\text{;}\)
    3. \(y=\mathrm{e}^{-x} \cos (3-x)\text{;}\)
    4. \(y=\arctan \frac{1-x^{2}}{1+x^{2}}\text{;}\)
    5. \(y=\mathrm{e}^{\sin x^{2}}\text{;}\)
    6. \(y=5^{\ln \tan x}\text{;}\)
    7. \(y=x \arccos \sqrt{1-x^{2}}\text{;}\)
    8. \(y=f\left(\arctan \frac{1}{x}\right)\text{,}\) 其中 \(f\) 可导.
  3. 设 \(y=y(x)\) 由下列方程所确定,
    1. \(x y+y^{2}-\cos y=1\text{,}\) 求 \(\mathrm{d} y\text{;}\)
    2. \(x^{3}+y^{3}-\sin 3 x+6 y=0\text{,}\) 求 \(\left.\mathrm{d} y\right|_{x=0}\text{.}\)
  4. 设 \(u, v\) 是 \(x\) 的可微函数, 求 \(\mathrm{d} y\text{.}\)
    1. \(y=u v^{-2}\text{;}\)
    2. \(y=\arctan \frac{u}{v}\text{;}\)
    3. \(y=\ln \left[\sin \left(u^{2}+v^{2}\right)\right]\text{;}\)
    4. \(y=f(u v), f\) 可导.
  5. 计算下列各式的近似值:
    1. \(\ln 1.002\text{;}\)
    2. \(\sqrt[3]{997}\text{;}\)
    3. \(\sin 29^{\circ}\text{.}\)
  6. 当 \(|x|\) 较小时,证明下列近似等式:
    1. \(\sin x \approx x\) (弧度);
    2. \(\displaystyle \arcsin x \approx x ;\)
    3. \(\tan x \approx x\text{;}\)
    4. \(\arctan x \approx x\text{;}\)
    5. \(\ln (1+x) \approx x\text{;}\)
    6. \(\mathrm{e}^{x} \approx 1+x\text{;}\)
    7. \((1+x)^{\alpha} \approx 1+\alpha x\text{.}\)
  7. 计算下列各式近似值:
    1. \(\sin 0.02\text{;}\)
    2. \(\arcsin 0.01\text{;}\)
    3. \(\mathrm{e}^{0.05}\text{;}\)
    4. \(\arctan 0.03\text{.}\)
  8. 设扇形的圆心角 \(\alpha=60^{\circ}\text{,}\)半径 \(r=100 \mathrm{~cm}\text{,}\)如果 \(r\) 不变, \(\alpha\) 减少 \(0.5^{\circ}\text{,}\) 问扇形面积约改变多少? 如果 \(\alpha\) 不变, \(r\) 增加 \(1 \mathrm{~cm}\text{,}\)问扇形面积约改变多少?
  9. 由电学知, 功率 \(P\) 与电压 \(U\) 、电阻 \(R\) 的关系是 \(P=\frac{U^{2}}{R}\text{,}\) 今有一额定功率 \(P=1 \mathrm{~kW}\) 的电炉接到电压 \(U=220 \mathrm{~V}\) 的电源上, 当电源波动不超过 \(5 \%\) 时, 引起电功率偏差额定的功率是多少?
  10. 计算球的体积 \(\mathrm{V}\) 精确至 \(1 \%\text{,}\)若根据所得的体积值推算球的半径 \(R\text{,}\)问 \(R\) 的相对误差是多少?
  11. 假设生产 \(x\) 台洗衣机的成本为 \(c(x)=20000+1000 x-x^{2}\) (元).
    1. 求生产前 100 台洗衣机的平均成本;
    2. 求当 100 台洗衣机生产出来时的边际成本;
    3. 证明当 100 台洗衣机生产出来时的边际成本近似等于在 100 台之后多生产一台洗衣机的成本,通过直接计算来求得生产第 101 台洗衣机的成本.
  12. 假设售出 \(x\) 台洗衣机的成本为 \(r(x)=200000\left(1-\frac{1}{x}\right)\) 元.
    1. 求生产出 100 台洗衣机的边际收人;
    2. 利用函数 \(r^{\prime}(x)\) 来估算从每周生产 100 台洗衣机到每周生产 101 台洗衣机的收人的增长;
    3. 求 \(x \rightarrow \infty\) 时 \(r^{\prime}(x)\) 的极限. 如何解释这个数的含义?
PrevTopNext