Example 4.5.1.
例 1 计算直线 \(y=a x+b\) 在任意一点处的曲率.
Solution.
解 因为 \(y^{\prime}=a, y^{\prime \prime}=0\text{,}\) 由曲率公式得到 \(K=0\text{.}\)
即直线上任意一点处的曲率都等于零, 这与直观上的 “直线不弯曲” 是一致的.
Section 4.5 曲率
实际问题中,常常需要研究曲线的弯曲程度. 如火车在转弯处,路轨需要适当的曲线来衔接,使火车能够平稳地转人弯道;钢梁的弯曲变形等都需要讨论曲线的弯曲程度. 因此,如何计算弯曲程度是非常必要的.
Subsection 4.5.1 弧微分
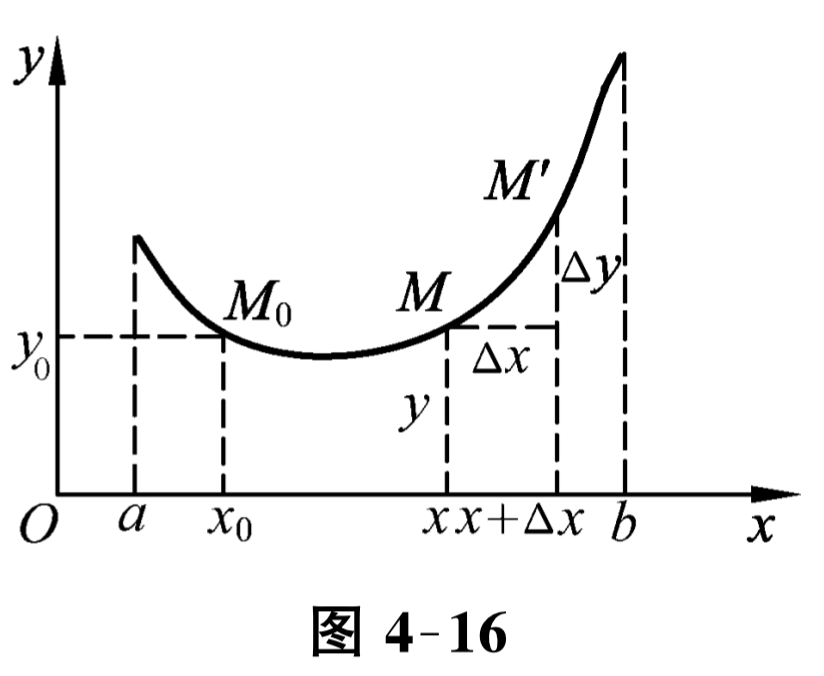
为了研究曲线的弯曲程度,首先介绍弧微分的概念. 为此先给出弧的定义: 设函数 \(y=f(x)\) 在区间 \((a, b)\) 内具有连续导数,在曲线 \(y=\) \(f(x)\) 上取固定点 \(M_{0}\left(x_{0}, y_{0}\right)\) 作为度量弧长的基点 (见图 4-16), 并规定依 \(x\) 增大的方向作为曲线的正向.对曲线上任一点 \(M(x, y)\text{,}\) 规定有向弧段 \(\overparen{M_{0} M}\) 的值 \(s\)如下: \(s\) 的绝对值等于弧 \(\overparen{M_{0} M}\) 的长度, 当 \(\overparen{M_{0} M}\) 的方向与曲线的正向一致时弧长 \(s>0\text{;}\) 相反时, 弧长 \(s<0\text{.}\)于是弧长 \(s\) 是 \(x\) 的函数,即 \(s=s(x)\text{.}\) 而且它是 \(x\) 的单调增加函数,下面来求 \(s(x)\) 的微分.
设 \(x, x+\Delta x\) 为 \((a, b)\) 内两个相邻的点, 它们在曲线 \(y=f(x)\) 上的对应点为 \(M, M^{\prime}\) (见图 4-16), 并设对应于 \(x\) 的增量 \(\Delta x\text{,}\) 弧长 \(s\) 的增量为 \(\Delta s\text{,}\) 那么
\begin{equation*}
\Delta s=\overparen{M_{0} M^{\prime}}-\overparen{M_{0} M}=\overparen{M M^{\prime}}
\end{equation*}
上式中,用有向弧段的记号,如 \(\overparen{M M^{\prime}}\) 表示该有向弧段的值,于是
\begin{equation*}
\begin{gathered}
\left(\frac{\Delta_{s}}{\Delta x}\right)^{2}=\left(\frac{\overparen{M M^{\prime}}}{\Delta x}\right)^{2}=\left(\frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|}\right)^{2} \cdot \frac{\left|M M^{\prime}\right|^{2}}{(\Delta x)^{2}}=\left(\frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|}\right)^{2} \cdot \frac{(\Delta x)^{2}+(\Delta y)^{2}}{(\Delta x)^{2}} \\
=\left(\frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|}\right)^{2}\left[1+\left(\frac{\Delta y}{\Delta x}\right)^{2}\right],
\end{gathered}
\end{equation*}
则
\begin{equation*}
\frac{\Delta s}{\Delta x}= \pm \sqrt{\left(\frac{M M^{\prime}}{\left|M M^{\prime}\right|}\right)^{2} \cdot\left[1+\left(\frac{\Delta y}{\Delta x}\right)^{2}\right] .}
\end{equation*}
因为 \(s=s(x)\) 是 \(x\) 的单调增加函数, 所以 \(\Delta s\) 与 \(\Delta x\) 同号, 即 \(\frac{\Delta s}{\Delta x}>0\text{,}\) 所以上式 中应取正号. 因此
\begin{equation*}
\frac{\Delta s}{\Delta x}=\frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|} \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}}
\end{equation*}
令 \(\Delta x \rightarrow 0\text{,}\) 则 \(M^{\prime} \rightarrow M\text{,}\) 又因为
\begin{equation*}
\lim\limits_{M^{\prime} \rightarrow M}\left|\frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|}\right|=1 \text { 及 } \lim\limits_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=y^{\prime} ,
\end{equation*}
所以按导数的定义得
\begin{equation*}
\frac{\mathrm{d} s}{\mathrm{~d} x}=\lim\limits_{\Delta x \rightarrow 0} \frac{\Delta s}{\Delta x}=\lim\limits_{\Delta x \rightarrow 0} \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^{2}} \cdot \lim\limits_{M^{\prime} \rightarrow M} \frac{\overparen{M M^{\prime}}}{\left|M M^{\prime}\right|}=\sqrt{1+y^{\prime 2}},
\end{equation*}
即
\begin{equation}
\mathrm{d} s=\sqrt{1+y^{\prime 2}} \mathrm{~d} x \text { 或 } \mathrm{d} s=\sqrt{(\mathrm{d} x)^{2}+(\mathrm{d} y)^{2}} \text {. }\tag{4.5.1}
\end{equation}
上式称为弧微分计算公式. 利用弧微分计算公式, 给出描述曲线弯曲程度的量——曲率的计算公式.
Subsection 4.5.2 曲率的计算公式
下面引入曲率的概念. 直线不弯曲, 半径较小的圆弯曲得比半径较大的圆明显些,而其他曲线不同部分有不同的弯曲程度.
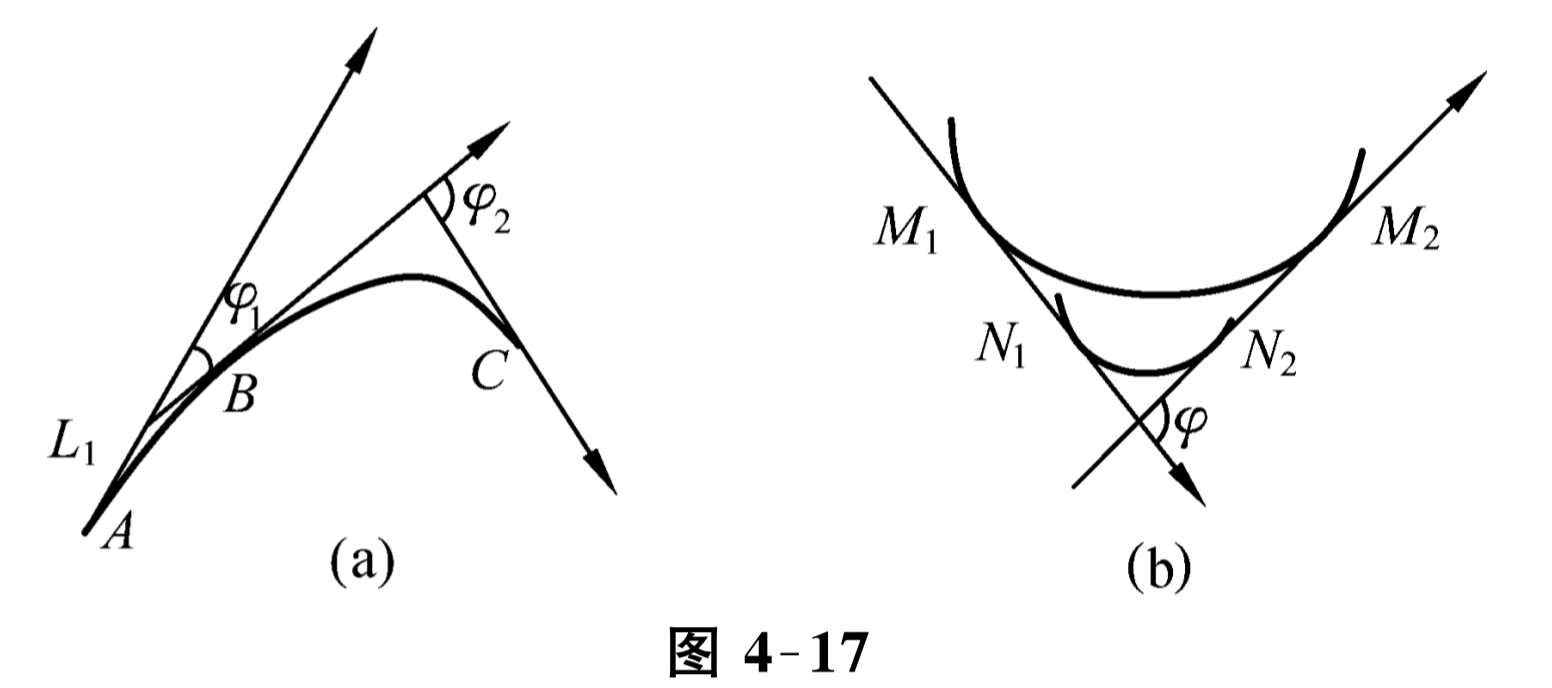
如图 4-17a 所示, 在曲线 \(L_{1}\)上分别取点 \(A, B, C\text{,}\) 且 \(\overparen{A B}=\) \(\overparen{B C}=\Delta s\text{.}\) 当动点沿着曲线由 \(A\)点向 \(B\) 点连续移动时, 曲线的切线转角为 \(\varphi_{1}\text{.}\) 当动点由 \(B\) 向 \(C\)移动时其切线的转角为 \(\varphi_{2}\text{,}\) 由图 4-17a 可见 \(\varphi_{2}>\varphi_{1}\text{.}\)
其原因为 \(\overparen{B C}\) 的弯曲程度比 \(\overparen{A B}\) 大. 但切线倾角变化的大小 \(\varphi\) 还不能完全反映曲线的弯曲程度. 例如图 4-17b 显示曲线的弯曲程度还与弧段的长度有关. 由此可见, 同样的弧长 \(\overparen{M M^{\prime}}=\Delta s\) 其弯曲程度和曲线弧 \(\overparen{M M^{\prime}}\) 两端点切线夹角 \(\varphi=\Delta \alpha\) 有关, \(\Delta \alpha\) 大, 曲线弯曲程度就大; 但对有相同的切线转角 \(\varphi=\Delta \alpha\text{,}\) 则弧长 \(\Delta s\) 越长,弯曲程度就越小. 为此, 用:
- \(\left|\frac{\Delta \alpha}{\Delta s}\right|\) 来描述曲线弧 \(\Delta s\) 的平均弯曲程度;
- 用 \(\lim\limits_{\Delta \rightarrow 0}\left|\frac{\Delta \alpha}{\Delta s}\right|\) 描写曲线在点 \(M\) 处的弯曲程度.
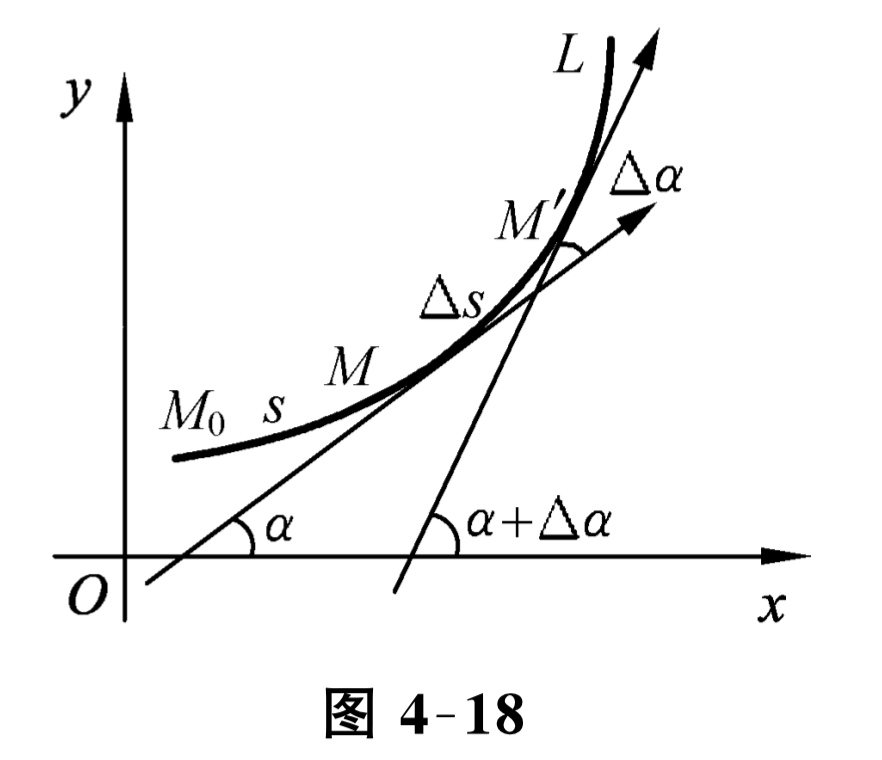
设曲线 \(L\) 具有连续转动的切线. 在曲线 \(L\) 上选定一点 \(M_{0}\) 作为度量弧长 \(s\) 的基点. 设曲线上点 \(M\) 对应于弧长 \(s, M\) 处切线的倾角为 \(\alpha\text{,}\) 曲线上另外一点 \(M^{\prime}\) 对应弧长 \(s+\Delta s\text{,}\) 在点 \(M^{\prime}\) 处切线的倾角为 \(\alpha+\Delta \alpha\) (见图 4-18), 那么, 弧段 \(\overparen{M M^{\prime}}\) 的长度为 \(|\Delta s|\text{,}\) 当动点从点 \(M\) 移动到点 \(M^{\prime}\) 时切线转过的角度为 \(|\Delta \alpha|\text{.}\)
比值 \(\frac{|\Delta \alpha|}{|\Delta s|}\) 表示了单位弧段上切线转角的大小.用它来刻画弧段 \(\overparen{M M^{\prime}}\) 的平均弯曲程度, 称为弧段 \(\overparen{M M^{\prime}}\) 的平均曲率, 记为 \(\bar{K}\text{,}\) 即
\begin{equation*}
\bar{K}=\frac{|\Delta \alpha|}{|\Delta s|}
\end{equation*}
当 \(\Delta s \rightarrow 0\text{,}\) 即 \(M \rightarrow M^{\prime}\) 时, 平均曲率 \(\bar{K}\) 的极限称为曲线 \(L\) 在点 \(M\) 处的曲率, 记为 \(K\text{,}\) 即
\begin{equation*}
K=\lim\limits_{\Delta s \rightarrow 0} \frac{|\Delta \alpha|}{|\Delta s|}
\end{equation*}
若 \(\lim\limits_{\Delta s \rightarrow 0} \frac{\Delta \alpha}{\Delta s}=\frac{\mathrm{d} \alpha}{\mathrm{d} s}\) 存在, 则
\begin{equation}
K=\left|\frac{\mathrm{d} \alpha}{\mathrm{d} s}\right|\tag{4.5.2}
\end{equation}
曲线在一点的曲率刻画了曲线在该点的弯曲程度. 下面给出计算曲率的公式.
设曲线的直角坐标方程为 \(y=f(x)\text{,}\) 且 \(f(x)\) 有二阶导数. 因为 \(y^{\prime}=\tan \alpha\text{,}\) 则
\begin{equation*}
\alpha=\arctan y^{\prime},
\end{equation*}
所以
\begin{equation*}
\frac{\mathrm{d} \alpha}{\mathrm{d} x}=\frac{y^{\prime \prime}}{1+y^{\prime 2}}
\end{equation*}
则有
\begin{equation*}
\mathrm{d} \alpha=\left(\frac{\mathrm{d} \alpha}{\mathrm{d} x}\right) \mathrm{d} x=\frac{y^{\prime \prime}}{1+y^{\prime 2}} \mathrm{~d} x
\end{equation*}
又由本节的弧微分
\begin{equation*}
\mathrm{d} s=\sqrt{1+y^{\prime 2}} \mathrm{~d} x,
\end{equation*}
所以由曲率的定义得到
\begin{equation}
K=\left|\frac{\mathrm{d} \alpha}{\mathrm{d} s}\right|=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}} .\tag{4.5.3}
\end{equation}
上式就是得到的曲率的计算公式.
Example 4.5.2.
例 2 计算圆 \(x^{2}+y^{2}=R^{2}\) 的曲率.
Solution.
解 因为 \(y= \pm \sqrt{R^{2}-x^{2}}\text{,}\) 所以
\begin{equation*}
\begin{gathered}
y^{\prime}=\frac{x}{\mp \sqrt{R^{2}-x^{2}}}, y^{\prime \prime}=\frac{R^{2}}{\left(R^{2}-x^{2}\right)^{\frac{3}{2}}}, \\
K=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{\frac{3}{2}}}=\frac{1}{R} .
\end{gathered}
\end{equation*}
该结论说明: (1) 圆上各点的弯曲程度相同; (2) 圆的半径越大,其曲线弧的弯曲程度越小.
设曲线由参数方程 \(\left\{\begin{array}{l}x=\varphi(t), \\ y=\psi(t)\end{array}\right.\) 给出, 则可利用由参数方程所确定的函数的求导法, 求出 \(y_{x}^{\prime}\) 及 \(y_{x}^{\prime \prime}\text{,}\) 代人公式 (3) 得
\begin{equation}
K=\frac{\left|\varphi^{\prime}(t) \psi^{\prime \prime}(t)-\varphi^{\prime \prime}(t) \psi^{\prime}(t)\right|}{\left[\varphi^{\prime 2}(t)+\psi^{\prime 2}(t)\right]^{\frac{3}{2}}} .\tag{4.5.4}
\end{equation}
如Example 4.5.2中, 圆的参数方程 \(\left\{\begin{array}{l}x=R \cos t, \\ y=R \sin t\end{array}\right.\) 代人(4.5.4), 即得 \(K=\frac{1}{R}\text{.}\)
Subsection 4.5.3 曲率圆
书中曾用切线的斜率作为函数的变化率, 即导数的几何解释. 此用圆的半径来作为曲率的几何尺度, 即为了更形象地表示曲率, 引人曲率圆的概念.
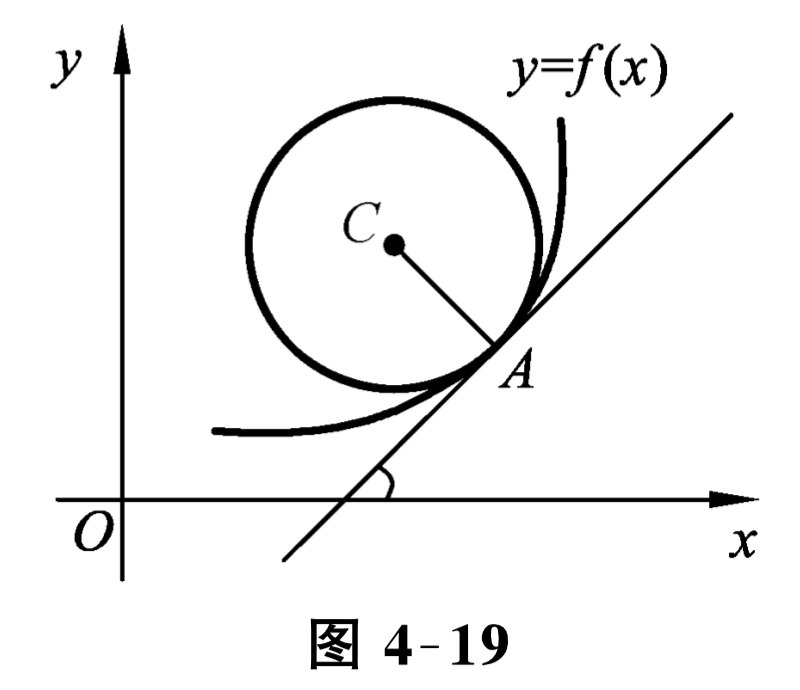
假定曲线 \(y=f(x)\) 在点 \(A\) 的曲率 \(K\) 不为零, 过点 \(A\) 引曲线的法线, 在曲线凹的一侧的法线上取点 \(C\text{,}\) 使 \(|A C|=\frac{1}{K}\text{,}\) 然后以 \(C\) 为中心, \(|A C|\) 为半径作一圆 (见图 4-19), 称这个圆为曲线在点 \(A\) 的曲率圆, 它的半径叫曲率半径, 圆心叫曲率中心.
通常, 若 \(K \neq 0\text{,}\) 则一点的曲率的倒数称为该点的曲率半径, 记为 \(\rho\text{,}\) 即 \(\rho=\frac{1}{K}\text{;}\) 若 \(K=0\text{,}\) 则该点的曲率半径规定为 \(+\infty\text{.}\)
曲率圆和曲线在点 \(A\) 显然是相切的, 并且有相同的凹向. 由于曲率圆的曲率等于半径的倒数, 所以它在点 \(A\) 与曲线也有相同的曲率. 因此, 在通过点 \(A\) 的一切圆中, 以曲率圆在点 \(A\) 附近与曲线的形状最为接近. 这就是在涉及有关曲线的凹凸性和曲率的实际问题中,常用曲率圆在点 \(A\) 附近的一段圆弧来代替曲线弧的理论依据。
曲率圆的概念不仅给出了曲率的几何直观解释, 而且在实际应用中, 经常要利用曲率圆或曲率半径.
Example 4.5.3.
例 3 计算曲线 \(y=\sin x\) 在 \(\left(\frac{\pi}{2}, 1\right)\) 处的曲率及曲率半径.
Solution.
解 \(y^{\prime}=\cos x, y^{\prime \prime}=-\sin x\text{,}\) 且 \(\left.y^{\prime}\right|_{x=\frac{\pi}{2}}=0,\left.y^{\prime \prime}\right|_{x=\frac{\pi}{2}}=-1\text{,}\) 所以
\begin{equation*}
K=\left.\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime 2}\right)^{3 / 2}}\right|_{x=\frac{\pi}{2}}=1, \rho=\frac{1}{K}=1
\end{equation*}
即这时曲率半径 \(\rho=1\text{.}\)
Example 4.5.4.
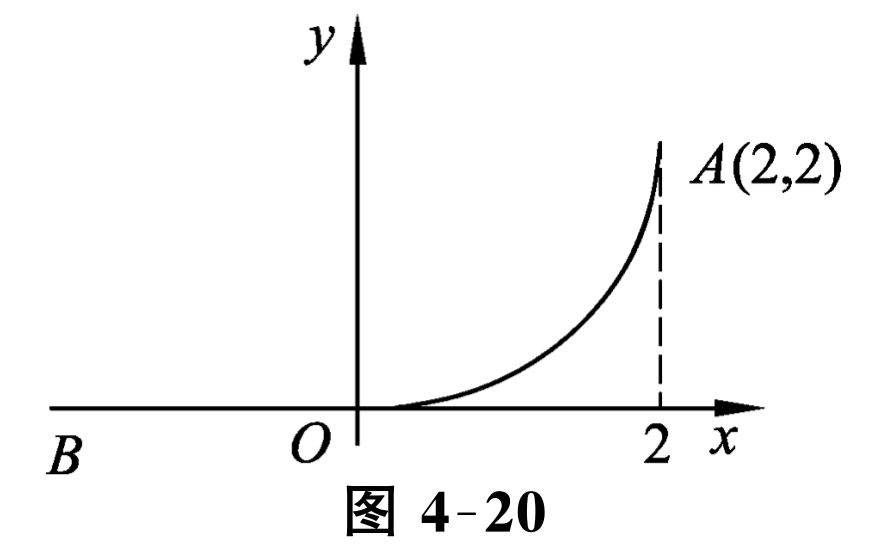
例 4 图 4-20 表示铁路由直轨 \(B O\) 转弯到点 \(A(2,2)\) 的一段线路. 因为火车的弯道一般是一个半径很大的圆弧, 但由直道转人弯道时不能直接将直道和圆弧相连, 必须通过一条过渡曲线转换成圆弧。关键是接合点处的曲率应相同, 只有这样才使火车经过接合点 \(O\) 处时不发生振荡.
因为由物理学知, 当一列火车在曲线轨道上以速度 \(v\) 运行时, 所产生的离心力为
\begin{equation*}
\frac{m v^{2}}{r}=m v^{2} k
\end{equation*}
其中 \(m\) 为火车的质量, \(r\) 为各点处的曲率半径, \(k\) 为曲率. 当 \(m, v\) 为常数时, 离心力随曲率 \(k\) 而变化. 当 \(k\) 不连续变化时, 离心力就发生间断而突变, 从而使列车产生振荡. 因此只有当曲率 \(k\) 连续变化时, 离心力也连续变化, 才不致于引起剧烈振动.
由此可见, 由于直线的曲率等于 0 , 所以应该选择最简单的曲线 \(y=f(x)\) 作为 \(\overparen{O A}\) 弧段, 使 \(B O A\) 成为连续、光滑、曲率连续变化的曲线. 特别是在接合点 \(O\) 处应满足下列条件:
(1) \(f(0)=0\text{;}\) (2) \(f^{\prime}(0)=0\text{;}\) (3) \(f^{\prime \prime}(0)=0\text{,}\) 即 \(k=0\text{;}\) (4) \(f(2)=2\text{,}\) 即曲线应通过点 \(A(2,2)\text{.}\)
易见,满足上述四个条件的最简单曲线应为三次多项式
\begin{equation*}
f(x)=a x^{3}+b x^{2}+c x+d,
\end{equation*}
其中 \(a, b, c, d\) 为待定常数. 根据上述四个条件恰能确定这四个常数, 即 \(\overparen{O A}\) 弧段的方程应为立方抛物线 \(y=\frac{1}{4} x^{3}\text{.}\) 它不是想像中的直接连接一段圆弧形状的曲线,而是要经过一条过渡曲线转换到圆弧。
Subsection 4.5.4 习题 4-5
-
求下列曲线在指定点的曲率和曲率半径:
- \(y=x^{3}+x\) 在 \((0,0)\) 处;
- \(y=\cos x\) 在 \(x=0\) 处;
- \(y=x^{2}-4 x+3\) 在顶点处;
- \(y=x+\ln x\) 在 \((1,1)\) 处.
- 求曲线 \(y=\frac{a}{4} x^{4}(a>0)\) 上各点处的曲率, 并求曲线上曲率最小、最大的点.
- 求曲线 \(y=a \ln \left(1-\frac{x^{2}}{a^{2}}\right)(a>0)\) 上各点处的曲率半径, 并求曲线上曲率半径最小的点.
- 一飞机沿抛物线 \(y=\frac{x^{2}}{10000}(y\) 轴铅直向上, 单位为 \(\mathrm{m}\) ) 作俯冲飞行, 在坐标原点 \(O\) 处飞机的速度为 \(200 \mathrm{~m} / \mathrm{s}\text{.}\) 飞行员体重 \(G=70 \mathrm{~kg}\text{,}\) 求飞机俯冲至最低点即原点 \(O\) 处时座椅对飞行员的作用力. (提示: 作匀速圆周运动的物体所受的向心力为 \(F=\frac{m v^{2}}{r}\text{,}\) 其中 \(m\) 为物体的质量, \(v\) 为它的速度, \(r\) 为圆的半径.)
