高等数学: 数字教材

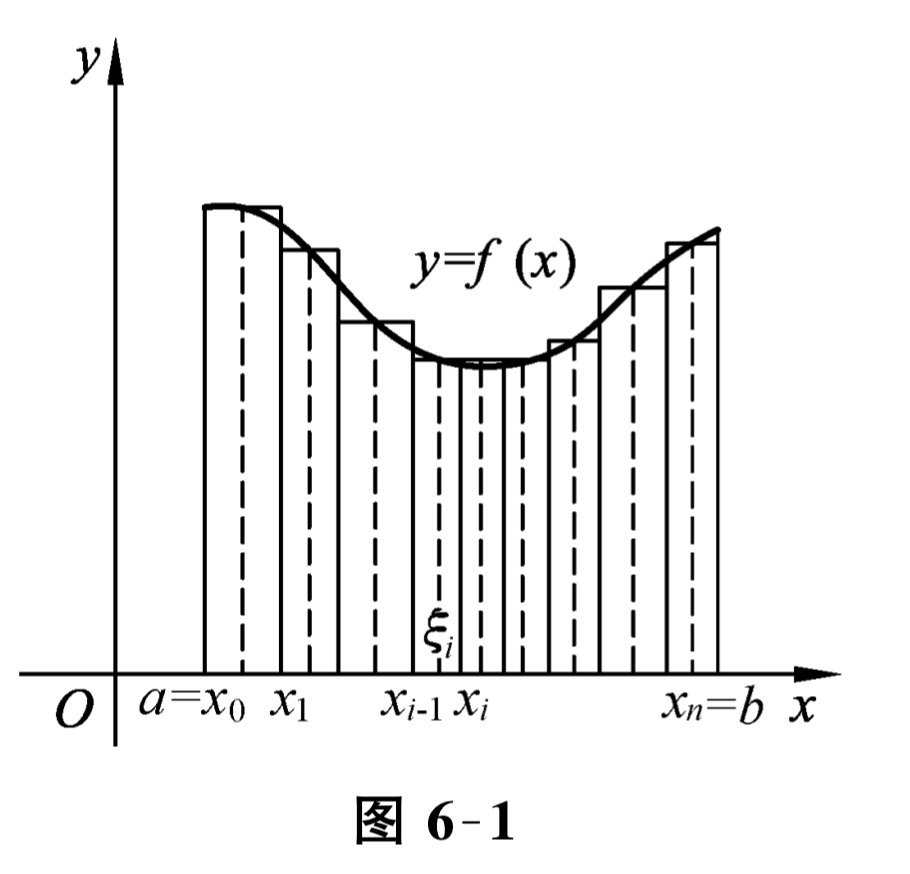
由于当矩形的高不变时, 它的面积可按公式:矩形面积 \(=\) 底 \(\times\) 高计算. 把曲边梯形与矩形比较,可以看到曲边梯形在底边上各点处的高 \(f(x)\) 在区间 \([a, b]\) 上是变动的, 所以它的面积不能直接利用矩形面积公式来计算,但注意到曲边梯形的高 \(f(x)\) 是 \(x\) 的连续函数,在很小一段区间上它的变化很小,特别是当小段区间非常小时, 高 \(f(x)\) 近似于不变. 因此,如果把区间 \([a, b]\) 划分为许多小区间,在每个小区间上用其中某一点处的高来近似代替该小区间上的小曲边梯形的变高, 那么每个小曲边梯形就可近似看成是小矩形,将所有这些小矩形面积之和作为曲边梯形面积的近似值, 并把区间细分下去,运用极限的思想就可求出曲边梯形的面积,下面分成四步来具体进行讨论. (1) 分割 在 \([a, b]\) 内任意插人 \(n-1\) 个分点: \(a=x_{0}<x_{1}<x_{2}<\cdots<x_{n-1}<x_{n}=\) \(b\text{,}\) 把区间 \([a, b]\) 分成 \(n\) 个小区间 \(\left[x_{0}, x_{1}\right],\left[x_{1}, x_{2}\right], \cdots,\left[x_{n-1}, x_{n}\right]\text{,}\) 其长度分别记为 \(\Delta x_{1}=x_{1}-x_{0}, \Delta x_{2}=x_{2}-x_{1}, \cdots, \Delta x_{n}=x_{n}-x_{n-1}\text{.}\) 过每个分点作平行于 \(y\) 轴的直线段, 于是原曲边梯形被分成 \(n\) 个小曲边梯形. (2)近似 当第 \(i\) 个小区间 \(\left[x_{i-1}, x_{i}\right]\) 的长度 \(\Delta x_{i}\) 很小时, \(f(x)\) 在其上变化也很小. 因此可以把该小区间上任意一点 \(\xi_{i}\) 处的函数值 \(f\left(\xi_{i}\right)\left(x_{i-1} \leqslant \xi_{i} \leqslant x_{i}\right)\) 作为第 \(i\) 个小曲边梯形的近似高度, 从而它的面积 \(\Delta S_{i}\) 可用以 \(f\left(\xi_{i}\right)\) 为高、 \(\Delta x_{i}\) 为底的小矩形面积近似代替, 即

(3)作和 把这 \(n\) 个小曲边梯形面积的近似值加起来, 即得曲边梯形面积 \(S\)的近似值 \(S_{n}\) :

(4)求极限 当区间 \([a, b]\) 被分得越细，且使每个区间的长度 \(\Delta x_{i}\) 越小, \(S\) 与 \(S_{n}\) 的误差就越小. 要得到精确值, 必须使每个小区间的长度趋于零, 记 \(\lambda=\max \limits_{i} \left\{\Delta x_{i}\right\}(k=1,2, \cdots, n)\) 为小区间的长度中的最大值. 当 \(\lambda \rightarrow 0\) 时, 所有小区间的长度 \(\Delta x_{i}\) 都趋于零, 运用极限思想, 便得

设某物体做直线运动, 已知速度 \(v=v(t)\) 是时间间隔 \(\left[T_{1}, T_{2}\right]\) 上 \(t\) 的连续函数,且 \(v(t) \geqslant 0\text{,}\)计算这段时间内物体所经过的路程 \(s\text{.}\) 做匀速直线运动的物体在时间段 \(t\) 内所经过的路程 \(s\) 就是它的速度 \(v\) 与时间 \(t\) 的乘积, 即 \(s=v t\text{.}\) 求做变速直线运动的物体从时刻 \(t=T_{1}\) 到时刻 \(t=T_{2}\) 这段时间内所经过的路程 \(s\text{.}\) 因速度 \(v(t)\) 随时间 \(t\) 的变化而变化,因此不能直接按上述公式计算, 但在很短的时间间隔内, 速度的变化很小, 近似于匀速. 这样就可求出这部分路程的近似值,仍用类似于求曲边梯形面积的方法来解决该问题. (1)分割 在时间间隔 \(\left[T_{1}, T_{2}\right]\) 内任意插人 \(n-1\) 个分点 \(T_{1}=t_{0}<t_{1}<t_{2}<\cdots<\) \(t_{n-1}<t_{n}=T_{2}\text{,}\) 把 \(\left[T_{1}, T_{2}\right]\) 分成 \(n\) 个小区间 \(\left[t_{0}, t_{1}\right],\left[t_{1}, t_{2}\right], \cdots,\left[t_{n-1}, t_{n}\right]\text{,}\) 且令 \(\Delta t_{i}=t_{i}-t_{i-1}(i=1,2, \cdots, n)\) 为各小区间的长度. 相应地,在各时段内物体经过的路程依次为 \(\Delta s_{1}, \Delta s_{2}, \cdots, \Delta s_{n}\text{.}\) (2)近似 在时间间隔 \(\left[t_{i-1}, t_{i}\right]\) 上任取一个时刻 \(\tau_{i}\text{,}\) 用 \(\tau_{i}\) 时刻的速度 \(v\left(\tau_{i}\right)\) 来代替 \(\left[t_{i-1}, t_{i}\right]\) 上各个时刻的速度，得 \(\Delta s_{i} \approx v\left(\tau_{i}\right) \Delta t_{i} \quad(i=1,2, \cdots, n)\text{.}\) (3)作和 物体在时间区间 \(\left[T_{1}, T_{2}\right]\) 内所经过的路程 \(s\) 的近似值 \(s_{n}\) 为物体在每个小时间段内所经过的路程的近似值之和, 即

(4)求极限 当分点的个数无限增加, 且最大一个小区间的长度趋于零时, 上述和式的极限即为物体从时刻 \(T_{1}\) 到时刻 \(T_{2}\) 以速度 \(v(t)\) 运动所经过的路程的精确值, 记 \(\lambda=\max \left\{\Delta t_{i}\right\}(i=1,2, \cdots, n)\text{,}\) 则