Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 8.3 任意项级数

各项符号不尽相同的级数, 称为任意项级数或一般项级数. 任意项级数的敛散性有相应的判别方法,但也常借助正项级数的审敛法来判别.

Subsection 8.3.1 交错级数与莱布尼茨审敛法

如果级数各项的符号正负交错出现, 这样的级数就称为交错级数, 即设 \(u_{n}>0\text{,}\) \(n=1,2,3, \cdots\text{,}\) 则级数
\begin{equation} \sum\limits_{n=1}^{\infty}(-1)^{n-1} u_{n}=u_{1}-u_{2}+u_{3}-u_{4}+\cdots+(-1)^{n-1} u_{n}+\cdots\tag{8.3.1} \end{equation}
就是交错级数. 交错级数还有一种可能就是
\begin{equation*} -u_{1}+u_{2}-u_{3}+u_{4}-\cdots+(-1)^{n} u_{n}+\cdots, \end{equation*}
该级数各项乘以 -1 就变成了级数 (8.3.1)的形式且不改变敛散性. 因此,不失一般性, 我们只需讨论级数 (8.3.1)的敛散性. 交错级数 (8.3.1)的特点是部分和 \(s_{n}\) 忽大忽小来回摆动:
\begin{equation*} s_{1}=u_{1}, s_{2}=s_{1}-u_{2}, s_{3}=s_{2}+u_{3}, \cdots, \end{equation*}
其摆动的幅度组成数列
\begin{equation*} u_{1}, u_{2}, u_{3}, u_{4}, \cdots . \end{equation*}
如果摆动的幅度不断变小且趋于 0 , 那么由图 8-4 可直观判断, \(s_{n}\) 一定趋于某数 \(s\text{.}\)下面介绍的审敛法很容易从以上几何诱导去理解.

Proof.

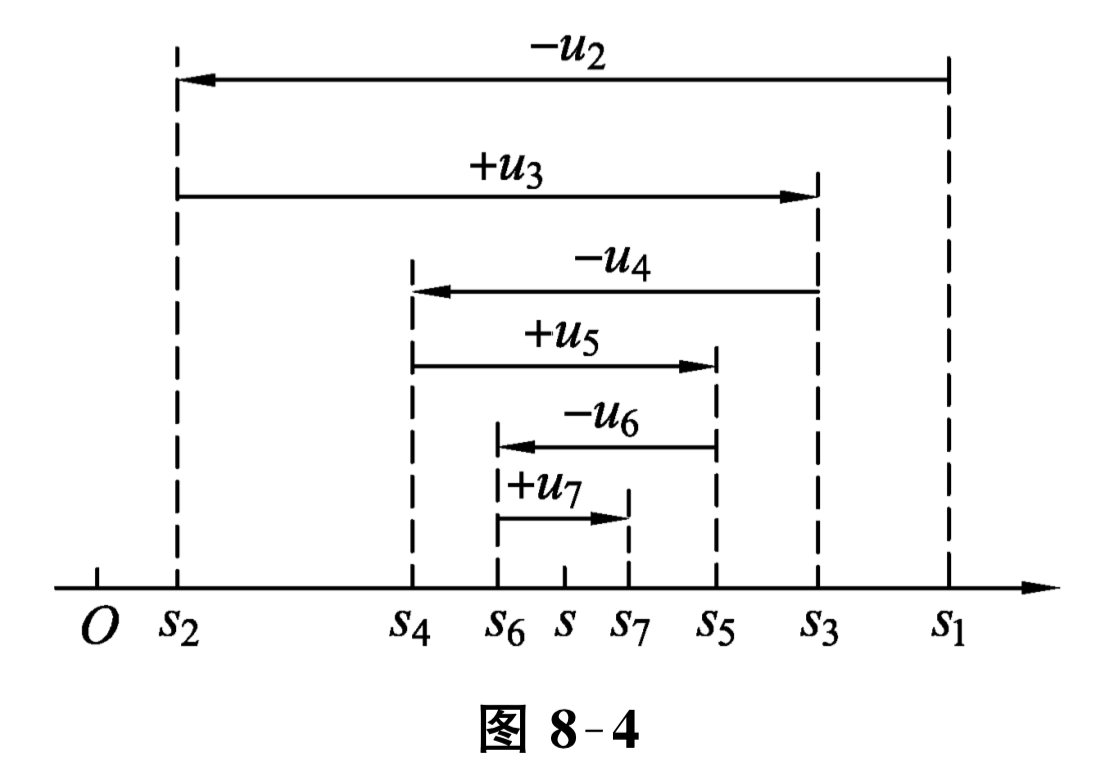
证 先证级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} u_{n}\) 前 \(2 n\) 项的部分和数列 \(\left\{s_{2 n}\right\}\) 的极限存在.
由 \(0<s_{2 n}=\left(u_{1}-u_{2}\right)+\left(u_{3}-u_{4}\right)+\cdots+\left(u_{2 n-1}-u_{2 n}\right)\) 及条件 (1) 可知 \(\left\{s_{2 n}\right\}\) 单调递增, 又 \(s_{2 n}=u_{1}-\left(u_{2}-u_{3}\right)-\cdots-\left(u_{2 n-2}-u_{2 n-1}\right)-u_{2 n}<u_{1}\text{,}\) 可知 \(\left\{s_{2 n}\right\}\) 有上界 \(u_{1}\text{.}\)由单调有界数列必有极限的定理知, \(\left\{s_{2 n}\right\}\) 存在极限, 记 \(\lim\limits_{n \rightarrow \infty} s_{2 n}=s\text{,}\) 显然 \(s \leqslant u_{1}\text{.}\)
再证级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} u_{n}\) 的前 \(2 n+1\) 项部分和数列 \(\left\{s_{2 n+1}\right\}\) 的极限存在.
由 \(s_{2 n+1}=s_{2 n}+u_{2 n+1}\) 及条件 (2), 得 \(\lim\limits_{n \rightarrow \infty} u_{2 n+1}=0\text{,}\) 所以
\begin{equation*} \lim\limits_{n \rightarrow \infty} s_{2 n+1}=\lim\limits_{n \rightarrow \infty} s_{2 n}=s \end{equation*}
因为级数的前偶数项的和与奇数项的和趋于同一极限 \(s\text{,}\) 所以有 \(\lim\limits_{n \rightarrow \infty} s_{n}=s\text{.}\) 这就证明了 i) 级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} u_{n}\) 收敛, 且 ii) 其和 \(s \leqslant u_{1}\text{.}\)
最后证明 iii) 其余项 \(r_{n}\) 的绝对值 \(\left|r_{n}\right| \leqslant u_{n+1}\text{.}\) 事实上,
\begin{equation*} r_{n}= \pm\left(u_{n+1}-u_{n+2}+\cdots\right), \end{equation*}
上式右端也是一个交错级数, 它满足莱布尼茨条件, 由上述证明知它收敛且其和
\begin{equation*} \left|r_{n}\right|=u_{n+1}-u_{n+2}+\cdots, \end{equation*}
小于级数的第一项, 也就是 \(\left|r_{n}\right| \leqslant u_{n+1}\text{.}\)
收敛的级数一定有和, 但求级数的和一般是一件很困难的事, 因此在实际应用中人们经常用级数的部分和 \(s_{n}\) 去近似级数的和 \(s\text{,}\) 用 \(s_{n}\) 近似代替 \(s\) 所产生的误差称为截断误差. 因此,截断误差就是余项 \(r_{n}\) 的绝对值. 对于满足莱布尼茨条件的交错级数而言, 截断误差可由 \(\left|r_{n}\right| \leqslant u_{n+1}\) 作估计.

Example 8.3.2.

例 1 证明级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{n^{p}}(p>0)\) 收敛,并估计其余项.
Solution.
证 该级数为交错级数. 又 \(u_{n}=\frac{1}{n^{p}} \geqslant \frac{1}{(n+1)^{p}}=u_{n+1}\text{,}\) 且 \(u_{n}=\frac{1}{n^{p}} \rightarrow 0(n \rightarrow \infty)\text{,}\) 根据莱布尼茨审敛法, 级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{n^{p}}(p>0)\) 收敛, 且 \(\left|r_{n}\right| \leqslant u_{n+1}=\frac{1}{(n+1)^{p}}\text{.}\)
特别地, 当 \(p=1\) 时,得收敛级数
\begin{equation*} \sum\limits_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{(-1)^{n-1}}{n}+\cdots . \end{equation*}
在后面会看到这一级数的和为 \(\ln 2\text{.}\)

Example 8.3.3.

例 2 判别级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{\ln n}{n}\) 的敛散性.
Solution.
解 这是一个交错级数, 用莱布尼茨审敛法Theorem 8.3.1. 这里 \(u_{n}=\frac{\ln n}{n}\text{,}\) 记 \(u_{n}=f(n)\text{,}\) 易证 \(f(x)=\frac{\ln x}{x}\) 在区间 \([3,+\infty)\) 内单调减少 \(\left(f^{\prime}(x)<0\right)\text{.}\) 因此当 \(n \geqslant 3\) 时, 有 \(u_{n} \geqslant u_{n+1}\text{;}\) 又 \(\lim\limits_{n \rightarrow \infty} u_{n}=\lim\limits_{n \rightarrow \infty} \frac{\ln n}{n}=0\text{,}\)故由莱布尼茨审敛法知 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{\ln n}{n}\) 收敛.

Example 8.3.4.

例 3 判别交错级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1}(\sqrt{n+1}-\sqrt{n})\) 的敛散性.
Solution.
解 设 \(f(x)=\sqrt{x+1}-\sqrt{x}\text{,}\) 则 \(f^{\prime}(x)=\frac{1}{2 \sqrt{x+1}}-\frac{1}{2 \sqrt{x}}=\frac{1}{2} \frac{\sqrt{x}-\sqrt{x+1}}{\sqrt{x(x+1)}}<0\text{,}\)由此可知 \(u_{n}=\sqrt{n+1}-\sqrt{n}>\sqrt{n+2}-\sqrt{n+1}=u_{n+1}\text{,}\) 又
\begin{equation*} \lim\limits_{n \rightarrow \infty}(\sqrt{n+1}-\sqrt{n})=\lim\limits_{n \rightarrow \infty} \frac{1}{\sqrt{n+1}+\sqrt{n}}=0 \end{equation*}
故所给级数收敛.

Subsection 8.3.2 任意项级数的绝对值审敛法

在任意项级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 中, 各项取绝对值就构成了一个正项级数 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\text{,}\) 这两个级数的收敛性有如下关系.

Proof.

证 令 \(v_{n}=\frac{1}{2}\left(u_{n}+\left|u_{n}\right|\right)(n=1,2, \cdots)\text{.}\) 显然 \(0 \leqslant v_{n} \leqslant\left|u_{n}\right|(n=1,2, \cdots)\text{.}\) 由正项级数的比较审敛法知, 级数 \(\sum\limits_{n=1}^{\infty} v_{n}\) 收敛, 从而级数 \(\sum\limits_{n=1}^{\infty} 2 v_{n}\) 也收敛. 而 \(u_{n}=2 v_{n}-\left|u_{n}\right|\text{,}\)所以 \(\sum\limits_{n=1}^{\infty} u_{n}=\sum\limits_{n=1}^{\infty}\left(2 v_{n}-\left|u_{n}\right|\right)\text{,}\) 由收敛级数的基本性质可知, 级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 收敛.
绝对值审敛法使得一大类任意项级数的敛散性判别问题转化成为正项级数的敛散性判别问题. 注意 绝对值审敛法的逆命题不成立, 即如果 \(\sum\limits_{n=1}^{\infty} u_{n}\) 收敛, 则 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) 未必收敛。 例如, 由Example 8.3.2知 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots\) 收敛, 但 \(\sum\limits_{n=1}^{\infty}\left|(-1)^{n-1} \frac{1}{n}\right|=\) \(\sum\limits_{n=1}^{\infty} \frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots\) 发散. 因此,收敛级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 可以分为两类: 一类是 \(\sum\limits_{n=1}^{\infty} u_{n}\) 收敛, 并且 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) 也收敛, 这时称 \(\sum\limits_{n=1}^{\infty} u_{n}\) 为绝对收敛;一类是 \(\sum\limits_{n=1}^{\infty} u_{n}\) 收敛,但 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) 发散,这时称 \(\sum\limits_{n=1}^{\infty} u_{n}\) 为条件收敛. 例如级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{n^{2}}\) 是绝对收敛级数, 而级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{n}\) 是条件收敛级数.

Example 8.3.6.

例 4 判别级数 \(\sum\limits_{n=1}^{\infty} \frac{\sin \frac{n \pi}{4}}{n^{5 / 4}}\) 的敛散性.
Solution.
解 这是任意项级数, 因为 \(\left|\frac{\sin \frac{n \pi}{4}}{n^{5 / 4}}\right| \leqslant \frac{1}{n^{5 / 4}}\text{,}\) 而正项级数 \(\sum\limits_{n=1}^{\infty} \frac{1}{n^{5 / 4}}\) 是 \(p=\frac{5}{4}>1\)的 \(p\)-级数, 收敛, 所以 \(\sum\limits_{n=1}^{\infty}\left|\frac{\sin \frac{n \pi}{4}}{n^{5 / 4}}\right|\) 也收敛. 因此, 级数 \(\sum\limits_{n=1}^{\infty} \frac{\sin \frac{n \pi}{4}}{n^{5 / 4}}\) 收敛且绝对收敛.
运用绝对值审敛法还需注意, 虽然不能因为级数 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) 发散就断定级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 也发散. 但是,如果我们判定级数 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) (正项级数) 发散用的是比值审敛 法或者根式审敛法, 就可以断定级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 肯定发散. 这是因为应用上述两种审敛法判定级数 \(\sum\limits_{n=1}^{\infty}\left|u_{n}\right|\) 发散的同时, 还有结论 \(\left|u_{n}\right| \rightarrow+\infty(n \rightarrow \infty)\text{,}\) 从而 \(u_{n} \nrightarrow 0\) \((n \rightarrow \infty)\text{,}\) 因此级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 也是发散的, 即若 \(\lim\limits_{n \rightarrow \infty} \frac{\left|u_{n+1}\right|}{\left|u_{n}\right|}=\rho>1\text{,}\) 或者 \(\lim\limits_{n \rightarrow \infty} \sqrt[n]{\left|u_{n}\right|}=\) \(\rho>1\text{,}\) 则 \(\sum\limits_{n=1}^{\infty} u_{n}\) 一定发散.

Example 8.3.7.

例 5 判别级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{2^{n}}\left(1+\frac{1}{n}\right)^{n^{2}}\) 的敛散性.
Solution.
解 由 \(\left|u_{n}\right|=\frac{1}{2^{n}}\left(1+\frac{1}{n}\right)^{n^{2}}\text{,}\) 有 \(\sqrt[n]{\left|u_{n}\right|}=\frac{1}{2}\left(1+\frac{1}{n}\right)^{n} \rightarrow \frac{\mathrm{e}}{2}(n \rightarrow \infty)\text{,}\) 而 \(\frac{\mathrm{e}}{2}>1\text{,}\) 可知 \(\left|u_{n}\right| \nrightarrow 0(n \rightarrow \infty)\text{,}\) 因此级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{2^{n}}\left(1+\frac{1}{n}\right)^{n^{2}}\) 发散.

Example 8.3.8.

例 6 判别级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{n} x^{n}(x>0)\) 的敛散性.
Solution.
解 由 \(\left|u_{n}\right|=\frac{x^{n}}{n}\text{,}\) 得 \(\lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}}{u_{n}}\right|=\lim\limits_{n \rightarrow \infty} \frac{x^{n+1}}{n+1} \cdot \frac{n}{x^{n}}=x\text{,}\) 由比值审敛法知:
当 \(x<1\) 时, 级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{n} x^{n}\) 绝对收敛;
当 \(x>1\) 时, 级数 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{n} x^{n}\) 发散;
当 \(x=1\) 时, 级数 \(\sum\limits_{n=1}^{\infty}\left|\frac{(-1)^{n}}{n}\right|\) 发散, 而 \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{n}\) 收敛, 故当 \(x=1\) 时, \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{1}{n} x^{n}\) 条件收敛.

Subsection 8.3.3 绝对收敛级数的性质

在 8.1.2 收敛级数性质中提到, 收敛级数可以任意加括号, 两个收敛级数也可以进行加减运算. 现在讨论收敛级数的项的重排 (交换项的次序) 问题以及级数相乘的问题.

Subsubsection 8.3.3.1 项的重排

有限项相加的和与相加的次序无关, 即加法满足交换律. 自然要问: 这个性质可否搬到无穷级数上来? 在这个问题上, 将看到条件收敛级数与绝对收敛级数有很大的区别. 在Example 8.3.2 中提到交错级数 \(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\cdots\) 收敛, 其和为 \(s\text{,}\) 所以该级数的部分和数列 \(\left\{s_{n}\right\}\) 收敛于 \(s\text{.}\) 现在将该级数按下述规则重新排列, 即在一个正项后接着排两个负项,得如下新级数：
\begin{equation} \underbrace{1-\frac{1}{2}-\frac{1}{4}}+\underbrace{\frac{1}{3}-\frac{1}{6}-\frac{1}{8}}+\cdots+\underbrace{\frac{1}{2 k-1}-\frac{1}{4 k-2}-\frac{1}{4 k}}+\cdots .\tag{8.3.2} \end{equation}
现证明它不具有原级数的和. 先考虑级数 (8.3.2) 前 \(3 k\) 项的部分和
\begin{equation*} \begin{aligned} \sigma_{3 k} & =\left(1-\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{6}-\frac{1}{8}\right)+\cdots+\left(\frac{1}{2 k-1}-\frac{1}{4 k-2}-\frac{1}{4 k}\right) \\ & =\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{6}-\frac{1}{8}\right)+\cdots+\left(\frac{1}{4 k-2}-\frac{1}{4 k}\right) \\ & =\frac{1}{2}\left[\left(1-\frac{1}{2}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\cdots+\left(\frac{1}{2 k-1}-\frac{1}{2 k}\right)\right] \\ & =\frac{1}{2}\left(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{2 k-1}-\frac{1}{2 k}\right)=\frac{1}{2} s_{2 k} \rightarrow \frac{1}{2} s(k \rightarrow \infty) . \end{aligned} \end{equation*}
另外,再考虑前 \(3 k+1\) 项的和与前 \(3 k+2\) 项的和
\begin{equation*} \begin{gathered} \sigma_{3 k+1}=\sigma_{3 k}+\frac{1}{2 k+1} \rightarrow \frac{1}{2} s(k \rightarrow \infty), \\ \sigma_{3 k+2}=\sigma_{3 k}+\frac{1}{2 k+1}-\frac{1}{4 k+2} \rightarrow \frac{1}{2} s(k \rightarrow \infty) . \end{gathered} \end{equation*}
因此新级数 (8.3.2) 的和为原级数的一半, 即
\begin{equation*} 1-\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{6}-\frac{1}{8}+\cdots+\frac{1}{2 k-1}-\frac{1}{4 k-2}-\frac{1}{4 k}+\cdots=\frac{1}{2} s . \end{equation*}
这个实例表明,收敛级数各项不一定满足“可交换性”, 改变相加次序可以影响它的和. 实际上可以证明: 对任一条件收敛级数, 通过适当地交换它各项的次序, 可以作成以任何定数 \(L\) 为和的收敛级数, 甚至也可以作成发散级数. 但对于绝对收敛级数,有如下重要性质.
Proof.
证明从略.

Subsubsection 8.3.3.2 级数的相乘

仿照两个有限项之和相乘的运算规则——可分配性, 我们可以得到两个级数的乘法运算: 一个级数中的每一项去遍乘另一个级数中的各项, 然后把全部乘积 (无穷多项) 相加. 设 \(\sum\limits_{n=1}^{\infty} u_{n}\) 和 \(\sum\limits_{n=1}^{\infty} v_{n}\) 为两个级数, 作出这两个级数各项所有可能的乘积 \(u_{i} v_{k}(i\text{,}\) \(k=1,2,3, \cdots)\text{,}\) 这些乘积也就是:
\begin{equation*} \begin{aligned} & u_{1} v_{1}, u_{1} v_{2}, u_{1} v_{3}, \cdots, u_{1} v_{i}, \cdots, \\ & u_{2} v_{1}, u_{2} v_{2}, u_{2} v_{3}, \cdots, u_{2} v_{i}, \cdots, \\ & u_{3} v_{1}, u_{3} v_{2}, u_{3} v_{3}, \cdots, u_{3} v_{i}, \cdots, \end{aligned} \end{equation*}
…… \(u_{k} v_{1}, u_{k} v_{2}, u_{k} v_{3}, \cdots, u_{k} v_{i}, \cdots\text{,}\) 这些乘积可以用很多的方式将它们排列成一个数列. 例如可以按 “对角线法”或“正方形法”将它们排列成下面形状的数列 (见图 8-5):
（对角线法） \(u_{1} v_{1} ; u_{1} v_{2}, u_{2} v_{1} ; u_{1} v_{3}, u_{2} v_{2}, u_{3} v_{1} ; \cdots\text{.}\) （正方形法） \(u_{1} v_{1} ; u_{1} v_{2}, u_{2} v_{2}, u_{2} v_{1} ; u_{1} v_{3}, u_{2} v_{3}, u_{3} v_{3}, u_{3} v_{2}, u_{3} v_{1} ; \cdots\text{.}\) 把上面排列好的数列用加号相连, 就组成无穷级数. 对于按 “对角线法” 排列所组成的级数
\begin{equation*} u_{1} v_{1}+\left(u_{1} v_{2}+u_{2} v_{1}\right)+\cdots+\left(u_{1} v_{n}+u_{2} v_{n-1}+\cdots+u_{n} v_{1}\right)+\cdots \end{equation*}
称为两级数 \(\sum\limits_{n=1}^{\infty} u_{n}\) 和 \(\sum\limits_{n=1}^{\infty} v_{n}\) 的柯西乘积.
Proof.
证明从略.

Subsection 8.3.4 习题 8-3

  1. 判别下列级数是否收敛? 如果是收敛的, 是绝对收敛还是条件收敛?
    (1) \(\sum\limits_{n=1}^{\infty} \sin \left(n \pi+\frac{1}{\ln n}\right)\text{;}\) (2) \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{2 n+1}{2^{n}}\text{;}\) (3) \(\sum\limits_{n=1}^{\infty}(-1)^{n}(\sqrt{n+1}-\sqrt{n})\text{;}\) (4) \(\sum\limits_{n=1}^{\infty}(-1)^{n+1} \frac{2 n^{2}}{n !}\text{;}\) (5) \(\sum\limits_{n=1}^{\infty}(-1)^{n} \frac{(n+1) !}{n^{n+1}}\text{;}\) (6) \(\sum\limits_{n=1}^{\infty}(-1)^{n-1} \frac{1}{3^{n}}\left(1+\frac{1}{n}\right)^{n^{2}}\text{.}\)
  2. 利用级数收敛的必要条件, 求下列数列的极限.
    1. \(\lim\limits_{n \rightarrow \infty} \frac{n^{n}}{(n !)^{2}}\text{;}\)
    2. \(\lim\limits_{n \rightarrow \infty} \frac{11 \cdot 12 \cdot \cdots \cdot(n+10)}{2 \cdot 5 \cdot \cdots \cdot(3 n-1)}\text{.}\)
PrevTopNext