Subsection 8.4.1 函数项级数
给定一个定义在集合 \(E\) 上的函数列
\begin{equation*}
u_{1}(x), u_{2}(x), u_{3}(x), \cdots, u_{n}(x), \cdots,
\end{equation*}
则式子
\begin{equation}
\sum\limits_{n=1}^{\infty} u_{n}(x)=u_{1}(x)+u_{2}(x)+u_{3}(x)+\cdots+u_{n}(x)+\cdots\tag{8.4.1}
\end{equation}
称为定义在 \(E\) 上函数项级数, 也简称为级数.
对于函数项级数, 如果 \(x\) 以固定的数值代人, 就成为常数项级数, 它可能收敛,也可能发散.
Definition 8.4.1.
定义 若当 \(x_{1} \in E\) 时, \(\sum\limits_{n=1}^{\infty} u_{n}\left(x_{1}\right)\) 收敛,则称 \(x_{1}\) 为 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的收敛点, 由 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的全部收敛点组成的集合称为 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的收敛域. 若当 \(x_{2} \in E\) 时, \(\sum\limits_{n=1}^{\infty} u_{n}\left(x_{2}\right)\) 发散,则称 \(x_{2}\) 为 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的发散点. 记 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的收敛域为 \(D\text{,}\)对每一个 \(x \in D\text{,}\) 级数 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 有和, 记 \(\sum\limits_{n=1}^{\infty} u_{n}(x)=s(x)\text{.}\) 这样就定义了集合 \(D\) 上的一个函数 \(s(x)\text{,}\) 称 \(s(x)\) 为 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 的和函数. 这时也称为 \(\sum\limits_{n=1}^{\infty} u_{n}(x)\) 收敛于 \(s(x), x \in D\text{.}\)
Example 8.4.2.
例 1 考虑公比是变量 \(x\) 的几何级数 \(\sum\limits_{n=1}^{\infty} x^{n-1}=1+x+x^{2}+\cdots+x^{n-1}+\cdots\text{,}\)由几何级数的结论,当 \(|x|<1\) 时收敛,当 \(|x| \geqslant 1\) 时发散,因此收敛点的全体是集 合 \(-1<x<1\text{,}\) 即收敛域是 \((-1,1)\text{,}\) 且
\begin{equation*}
\sum\limits_{n=1}^{\infty} x^{n-1}=\frac{1}{1-x}, x \in(-1,1)
\end{equation*}
因此,在 \((-1,1)\) 内, \(\sum\limits_{n=1}^{\infty} x^{n-1}\) 的和函数是 \(\frac{1}{1-x}\text{.}\)
值得注意的是, 这个级数的定义域是 \((-\infty,+\infty)\text{,}\) 函数 \(\frac{1}{1-x}\) 定义域是 \((-\infty, 1) \cup(1,+\infty)\text{,}\) 但只有在收敛域 \((-1,1)\) 内, \(\frac{1}{1-x}\) 才是 \(\sum\limits_{n=1}^{\infty} x^{n-1}\) 的和函数, 即才有 \(\sum\limits_{n=1}^{\infty} x^{n-1}=\frac{1}{1-x}\text{.}\) 所以在写收敛的函数项级数等于其和函数时, 必须注明其收敛域。
Example 8.4.3.
例 2 考虑级数 \(\sum\limits_{n=1}^{\infty} \frac{\sin n x}{n^{2}}=\frac{\sin x}{1^{2}}+\frac{\sin 2 x}{2^{2}}+\cdots+\frac{\sin n x}{n^{2}}+\cdots\) 的收敛域.
Solution.
解 因为 \(\left|\frac{\sin n x}{n^{2}}\right| \leqslant \frac{1}{n^{2}}, x \in(-\infty,+\infty)\text{,}\) 又 \(\sum\limits_{n=1}^{\infty} \frac{1}{n^{2}}\) 收敛, 所以收敛域是 \((-\infty,+\infty)\text{.}\)
下面将主要研究两类重要的函数项级数: 幂级数和傅里叶级数.
Subsection 8.4.2 幂级数与幂级数的收敛区间
在函数项级数中, 最简单、最重要的一类级数就是幂级数, 它在数学的理论和应用中都很重要. 一般把形如
\begin{equation}
\begin{aligned}
\sum\limits_{n=0}^{\infty} a_{n}\left(x-x_{0}\right)^{n}= & a_{0}+a_{1}\left(x-x_{0}\right)+a_{2}\left(x-x_{0}\right)^{2}+\cdots+ \\
& a_{n}\left(x-x_{0}\right)^{n}+\cdots
\end{aligned}\tag{8.4.2}
\end{equation}
的级数称为 \(\left(x-x_{0}\right)\) 的幂级数. 若 \(x_{0}=0\text{,}\) 则级数
\begin{equation}
\sum\limits_{n=0}^{\infty} a_{n} x^{n}=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}+\cdots\tag{8.4.3}
\end{equation}
是 \(x\) 的幂级数.
在式
(8.4.2)中, 如果令
\(t=x-x_{0}\text{,}\) 就得
\begin{equation*}
\sum\limits_{n=0}^{\infty} a_{n}\left(x-x_{0}\right)^{n}=\sum\limits_{n=0}^{\infty} a_{n} t^{n}
\end{equation*}
因此,下面着重研究幂级数
(8.4.3) 的性质. 首先需要考虑的问题是: 幂级数
(8.4.3) 在哪些点上收敛,收敛域有何特征, 这就是幂级数的收敛性问题. 显然当
\(x=0\) 时,幂级数
(8.4.3) 一定收敛, 也就是说, 幂级数总有收敛点. 由
Example 8.4.2 已经知道, 幂级数
\(\sum\limits_{n=1}^{\infty} x^{n}\) 的收敛域为
\((-1,1)\text{.}\) 为了进一步研究,再看一个例子.
Example 8.4.4.
例 3 求幂级数 \(\sum\limits_{n=1}^{\infty} \frac{1}{n \cdot 2^{n}} x^{n}\) 的收敛域.
Solution.
解 \(x\) 可以取任意数, 各项取绝对值后由正项级数比值审敛法得
\begin{equation*}
\left|\frac{u_{n+1}(x)}{u_{n}(x)}\right|=\left|\frac{x^{n+1}}{(n+1) \cdot 2^{n+1}} \cdot \frac{n \cdot 2^{n}}{x^{n}}\right|=\frac{n}{n+1} \frac{|x|}{2} \rightarrow \frac{|x|}{2}(n \rightarrow \infty) .
\end{equation*}
当 \(|x|<2\) 时,原级数绝对收敛,当 \(|x|>2\) 时发散.
当 \(x=2\) 时, 级数成为 \(1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}+\cdots\text{,}\) 级数是发散的.
当 \(x=-2\) 时, 级数成为 \(-1+\frac{1}{2}-\frac{1}{3}+\cdots+(-1)^{n} \frac{1}{n}+\cdots\text{,}\) 级数是收敛的.
所以级数的收敛域为 \(-2 \leqslant x<2\text{.}\)
Theorem 8.4.5.
定理
\(\mathbf{1}\) (阿贝尔 (Abel) 定理) 若幂级数
(8.4.3) 在点
\(x_{1} \neq 0\) 处收敛,则对满足不等式
\(|x|<\left|x_{1}\right|\) 的任何
\(x\text{,}\)幂级数
(8.4.3) 收敛且绝对收敛; 若幂级数
(8.4.3) 在点
\(x_{2}\) 发散,则对满足不等式
\(|x|>\left|x_{2}\right|\) 的任何
\(x\text{,}\)幂级数
(8.4.3) 也发散.
Proof.
证 由于级数 \(\sum\limits_{n=1}^{\infty} a_{n} x_{1}^{n}\) 收敛, 根据级数收敛的必要条件知 : \(\lim\limits_{n \rightarrow \infty} a_{n} x_{1}^{n}=0\text{.}\) 由收敛数列的有界性知, 数列 \(\left\{a_{n} x_{1}^{n}\right\}\) 有界, 即存在正数 \(M\text{,}\) 使得 \(\left|a_{n} x_{1}^{n}\right| \leqslant M, n=0,1\text{,}\) \(2, \cdots\text{.}\) 因此, 当 \(|x|<\left|x_{1}\right|\) 时有
\begin{equation*}
\left|a_{n} x^{n}\right|=\left|a_{n} x_{1}^{n} \cdot\left(\frac{x}{x_{1}}\right)^{n}\right|<M\left|\frac{x}{x_{1}}\right|^{n}, \quad n=0,1,2, \cdots .
\end{equation*}
因为 \(\left|\frac{x}{x_{1}}\right|<1\text{,}\) 几何级数
\begin{equation*}
M+M\left|\frac{x}{x_{1}}\right|+M\left|\frac{x}{x_{1}}\right|^{2}+\cdots+M\left|\frac{x}{x_{1}}\right|^{n}+\cdots
\end{equation*}
收敛, 所以由正项级数的比较审敛法得, 当
\(|x|<\left|x_{1}\right|\) 时,
\(\sum\limits_{n=0}^{\infty}\left|a_{n} x^{n}\right|\) 收敛, 即幂级数
(8.4.3) 绝对收敛.
现在用反证法证明定理的第二部分.
假设存在
\(x_{1},\left|x_{1}\right|>\left|x_{2}\right|\text{,}\) 使得幂级数
(8.4.3) 在
\(x_{1}\) 收敛. 由第一部分证明知, 由于
\(\left|x_{2}\right|<\left|x_{1}\right|\text{,}\) 所以幂级数
(8.4.3) 在点
\(x_{2}\) 收敛,这与假设矛盾, 从而命题成立.
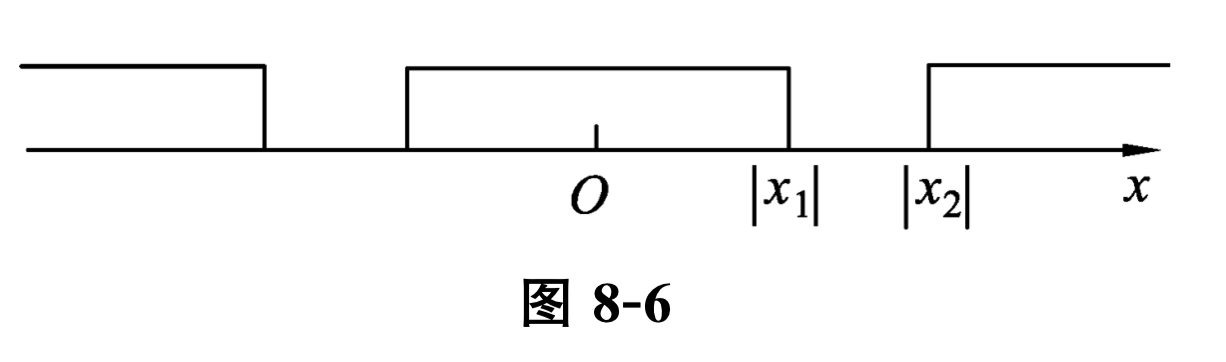
现在假设幂级数
(8.4.3) 在点
\(x_{1}\) 收敛,在点
\(x_{2}\) 发散. 由阿贝尔定理,
\(\left|x_{1}\right|<\left|x_{2}\right|\text{,}\)并且幂级数
(8.4.3) 在
\(|x|<\left|x_{1}\right|\) 时收敛,在
\(|x|>\left|x_{2}\right|\) 时发散(见图 8-6). 再考察幂级数
(8.4.3) 在
\(\left|x_{1}\right|\) 与
\(\left|x_{2}\right|\) 之间各点的敛散性, 根据阿贝尔定理知, 一定存在一点
\(x_{0}\text{,}\) 幂级数
(8.4.3) 在
\(|x|<\left|x_{0}\right|\) 时收敛, 在
\(|x|>\left|x_{0}\right|\) 时发散. 令 \(\left|x_{0}\right|=R,(-R, R)\) 称为幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 的收敛区间, \(R\) 称为该幂级数的收敛半径.
为了方便起见, 补充规定: 若幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 在 \((-\infty,+\infty)\) 内每一点都收敛,则称收敛区间为 \((-\infty,+\infty)\text{,}\) 收敛半径为 \(R=+\infty\text{;}\) 若幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 只在 \(x=0\)收敛, 则称收敛半径为 \(R=0\text{.}\) 于是, 所有的幂级数都有收敛半径.
对于幂级数
(8.4.2), 即
\(\sum\limits_{n=0}^{\infty} a_{n}\left(x-x_{0}\right)^{n}\text{,}\) 用变换
\(t=x-x_{0}\) 可将其化为幂级数
\(\sum\limits_{n=0}^{\infty} a_{n} t^{n}\text{,}\) 所以,若幂级数
(8.4.2) 存在非
\(x_{0}\) 的收敛点和发散点, 则必定存在正数
\(R>0\text{,}\)使得当
\(\left|x-x_{0}\right|<R\) 时幂级数
(8.4.2) 绝对收敛, 当
\(\left|x-x_{0}\right|>R\) 时幂级数
(8.4.2)发散. 此时, 称
\(\left(x_{0}-R, x_{0}+R\right)\) 为幂级数
(8.4.2)的收敛区间,
\(R\) 称为幂级数
(8.4.2)的收敛半径.
注意 收敛区间与收敛域是两个不同的概念. 收敛区间是开区间,不包含区间端点, 而若幂级数在收敛区间的某个端点收敛,则它的收敛域就包含该端点, 所以幂级数的收敛域可能比收敛区间多一个或两个端点. 当收敛半径为 \(+\infty\) 时, 收敛区间 \((-\infty,+\infty)\) 即为收敛域.
因为每一个幂级数由它的系数 \(a_{n}(n=0,1,2, \cdots)\) 所确定, 所以幂级数的收敛半径 \(R\) 也是由幂级数的系数来确定的. 下面给出幂级数收敛半径的计算公式.
Theorem 8.4.6.
定理 2 设幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 从某一项以后所有的 \(a_{n}\) 均不为 0 . 若
\begin{equation}
\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|=\rho\left(\text { 或 } \lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|=+\infty \text {, 此时记 } \rho=+\infty\right),\tag{8.4.4}
\end{equation}
则 : (i) 当 \(0<\rho<+\infty\) 时, 幂级数的收敛半径 \(R=1 / \rho\text{;}\)
(ii)当 \(\rho=0\) 时,幂级数的收敛半径 \(R=+\infty\text{;}\)
(iii)当 \(\rho=+\infty\) 时, 幂级数的收敛半径为 \(R=0\text{.}\)
Proof.
证 考虑幂级数各项取绝对值所成的级数
\begin{equation}
\left|a_{0}\right|+\left|a_{1} x\right|+\left|a_{2} x^{2}\right|+\left|a_{3} x^{3}\right|+\cdots+\left|a_{n} x^{n}\right|+\cdots .\tag{8.4.5}
\end{equation}
因为
\begin{equation*}
\lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}(x)}{u_{n}(x)}\right|=\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1} x^{n+1}}{a_{n} x^{n}}\right|=\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right| \cdot|x|=\rho \cdot|x|,
\end{equation*}
于是, 由比值审敛法得: (i) 若 \(0<\rho<+\infty\text{,}\) 则当 \(\rho|x|<1\text{,}\) 即 \(|x|<\frac{1}{\rho}\) 时, 幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 绝对收敛, 当 \(\rho|x|>1\text{,}\) 即 \(|x|>\frac{1}{\rho}\) 时, 幂级数 \(\sum\limits_{n=0}^{\infty} a_{n} x^{n}\) 发散. 因此收敛半径为 \(R=\frac{1}{\rho}\text{.}\) (ii) 若 \(\rho=0\text{,}\) 则对任意 \(x, \rho|x|=0<1\text{,}\) 即对任意 \(x\) 收敛, 因此 \(R=+\infty\text{.}\) (iii) 若 \(\rho=+\infty\text{,}\) 即 \(\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|=+\infty\text{,}\) 则对任何 \(x \neq 0\text{,}\) 都有 \(\lim\limits_{n \rightarrow \infty}\left|\frac{u_{n+1}(x)}{u_{n}(x)}\right|=\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right| \cdot|x|=+\infty\text{,}\) 所以对任何 \(x \neq 0\text{,}\) 幂级数发散, 因此 \(R=0\text{.}\)
Example 8.4.7.
例 4 已知 \(\sum\limits_{n=0}^{\infty} \frac{x^{n}}{n !}\text{,}\) 求收敛区间.
Solution.
解 因为 \(\left|\frac{a_{n+1}}{a_{n}}\right|=\frac{1}{(n+1) !} \cdot \frac{n !}{1}=\frac{1}{n+1} \rightarrow 0(n \rightarrow \infty)\text{,}\) 即 \(\rho=0\text{,}\) 所以收敛半径 \(R=+\infty\text{,}\) 从而收敛区间是 \((-\infty,+\infty)\text{.}\)
Example 8.4.8.
例 5 求 \(\sum\limits_{n=0}^{\infty} n ! x^{n}\) 的收敛半径、收敛区间和收敛域.
Solution.
解 因为 \(\left|\frac{a_{n+1}}{a_{n}}\right|=\frac{(n+1) !}{n !}=n+1 \rightarrow+\infty(n \rightarrow \infty)\text{,}\) 所以收敛半径 \(R=0\text{,}\) 幂级数对任何 \(x \neq 0\) 发散, 仅在 \(x=0\) 点收敛, 故收敛域为一点 \(x=0\text{.}\)
Example 8.4.9.
例 6 已知 \(\sum\limits_{n=1}^{\infty} \frac{3^{n}+(-2)^{n}}{n} x^{n}\text{,}\)求收敛半径、收敛区间和收敛域.
Solution.
解 这个幂级数所有的 \(a_{n} \neq 0\text{,}\) 可用上述求收敛半径的公式.
因为
\begin{equation*}
\rho=\lim\limits_{n \rightarrow \infty}\left|\frac{a_{n+1}}{a_{n}}\right|=\lim\limits_{n \rightarrow \infty} \frac{3^{n+1}+(-2)^{n+1}}{n+1} \cdot \frac{n}{3^{n}+(-2)^{n}}=3,
\end{equation*}
所以收敛半径 \(R=\frac{1}{\rho}=\frac{1}{3}\text{,}\) 收敛区间为 \(\left(-\frac{1}{3}, \frac{1}{3}\right)\text{.}\)
再考虑收敛区间的端点. 当 \(x=-\frac{1}{3}\) 时,幂级数成为
\begin{equation*}
\sum\limits_{n=1}^{\infty} \frac{3^{n}+(-2)^{n}}{n}\left(-\frac{1}{3}\right)^{n}=\sum\limits_{n=1}^{\infty} \frac{(-1)^{n}+\left(\frac{2}{3}\right)^{n}}{n} .
\end{equation*}
由于级数 \(\sum\limits_{n=1}^{\infty} \frac{(-1)^{n}}{n}\) 收敛(利用莱布尼茨审敛法), \(\sum\limits_{n=1}^{\infty} \frac{1}{n}\left(\frac{2}{3}\right)^{n}\) 收敛(利用比值审敛法), 因此原级数在 \(x=-\frac{1}{3}\) 处收敛. 当 \(x=\frac{1}{3}\) 时, 幂级数成为
\begin{equation*}
\sum\limits_{n=1}^{\infty} \frac{3^{n}+(-2)^{n}}{n}\left(\frac{1}{3}\right)^{n}=\sum\limits_{n=1}^{\infty} \frac{1+\left(-\frac{2}{3}\right)^{n}}{n}
\end{equation*}
由于调和级数 \(\sum\limits_{n=1}^{\infty} \frac{1}{n}\) 发散, \(\sum\limits_{n=1}^{\infty} \frac{1}{n}\left(-\frac{2}{3}\right)^{n}\) 收敛(绝对收敛), 故原级数在 \(x=\frac{1}{3}\) 处发散. 因此,原幂级数的收敛域是 \(\left[-\frac{1}{3}, \frac{1}{3}\right)\text{.}\)
Example 8.4.10.
例 7 求幂级数 \(\sum\limits_{n=1}^{\infty} \frac{(x+1)^{n}}{n^{2}}\) 的收敛半径、收敛区间和收敛域.
Solution.
解 这是在 \(x_{0}=-1\) 点的幂级数.
\begin{equation*}
\left|\frac{a_{n+1}}{a_{n}}\right|=\frac{1}{(n+1)^{2}} \cdot \frac{n^{2}}{1} \rightarrow 1
\end{equation*}
收敛半径 \(R=1\text{,}\) 收敛区间为 \(|x+1|<1\text{,}\) 即 \(-1<x+1<1\) 或 \((-2,0)\text{.}\)
当 \(x=-2\) 时,幂级数成为 \(\sum\limits_{n=0}^{\infty} \frac{(-1)^{n}}{n^{2}}=-1+\frac{1}{2^{2}}-\frac{1}{3^{2}}+\cdots+(-1)^{n} \frac{1}{n^{2}}+\cdots\text{,}\)收敛;
当 \(x=0\) 时,幂级数成为 \(\sum\limits_{n=1}^{\infty} \frac{1}{n^{2}}=1+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\cdots+\frac{1}{n^{2}}+\cdots\text{,}\) 收敛.
因此所给级数的收敛域为 \([-2,0]\text{.}\)
注意 因为上述求收敛半径的公式用 \(a_{n}\) 作除数,所以如果不满足从某一项以后的所有 \(a_{n}\) 均不为 0 的条件, 就不能应用这个公式. 如 \(\sum\limits_{n=0}^{\infty} a_{2 n} x^{2 n}\text{,}\) 所有奇数次幂的系数都为 0 , 即 \(a_{1}=a_{3}=a_{5}=\cdots=0\text{;}\) 又如 \(\sum\limits_{n=0}^{\infty} a_{2 n-1} x^{2 n-1}\text{,}\) 所有偶数次幂的系数都为 0 , 即 \(a_{0}=a_{2}=a_{4}=\cdots=0\text{,}\) 都不能直接利用上述公式求收敛半径. 对于这种情形, 可直接用比值审敛法来求收敛半径.
Example 8.4.11.
例 8 求幂级数 \(\sum\limits_{n=1}^{\infty} \frac{x^{2 n-1}}{3^{n-1}(2 n-1)}\) 的收敛半径、收敛区间和收敛域.
Solution.
解 幂级数中常数项及偶数幕的系数均为 0 , 因此不能用上述求收敛半径的公式,可直接对它的绝对值级数应用比值审敛法:
\begin{equation*}
\left|\frac{u_{n+1}(x)}{u_{n}(x)}\right|=\left|\frac{x^{2 n+1}}{3^{n}(2 n+1)} \cdot \frac{3^{n-1}(2 n-1)}{x^{2 n-1}}\right|=\frac{1}{3} \cdot \frac{2 n-1}{2 n+1}|x|^{2} \rightarrow \frac{1}{3}|x|^{2}(n \rightarrow \infty) .
\end{equation*}
当 \(\frac{1}{3}|x|^{2}<1\text{,}\) 即 \(|x|<\sqrt{3}\) 时绝对收敛; 当 \(\frac{1}{3}|x|^{2}>1\text{,}\) 即 \(|x|>\sqrt{3}\) 时发散. 故收敛半径 \(R=\sqrt{3}\text{,}\) 收敛区间为 \(|x|<\sqrt{3}\text{,}\) 即 \((-\sqrt{3}, \sqrt{3})\text{.}\)
当 \(x=-\sqrt{3}\) 时, 幂级数成为 \(\sum\limits_{n=1}^{\infty}(-1)^{2 n-1} \frac{\sqrt{3}}{2 n-1}=\sum\limits_{n=1}^{\infty} \frac{-\sqrt{3}}{2 n-1}\text{,}\) 发散;
当 \(x=\sqrt{3}\) 时,幂级数成为 \(\sum\limits_{n=1}^{\infty} \frac{\sqrt{3}}{2 n-1}\text{,}\) 发散. 因此,该幂级数的收敛域是 \((-\sqrt{3}, \sqrt{3})\text{.}\)