Definition 4.3.1.
定义 1 设函数 \(f(x)\) 在区间 \(I\) 上可导,如果该函数在 \(I\) 上的曲线都位于它的每一点处切线的上方, 那么称曲线 \(y=f(x)\) 在区间 \(I\) 上是凹的 (简称凹弧); 如果在区间 \(I\) 上曲线都位于它的每一点处的切线的下方, 那么称曲线 \(y=f(x)\) 在区间 \(I\) 上是凸的 (简称凸弧).
Section 4.3 曲线的凹凸性和拐点
Subsection 4.3.1 曲线的凹凸性和拐点
曲线除了上升下降, 还有凹凸的性态.例如, 如图 4-11 所示, 观察函数 \(y=\sin x\text{,}\) \(x \in(-\pi, \pi)\) 的图形的形状,在 \((-\pi, 0)\) 上曲线是向上弯曲的, 称为是凹的; 在 \((0, \pi)\) 上曲线是向下弯曲的, 称为是凸的, 这两段曲线的分界点为 \(O(0,0)\text{.}\) 当曲线是凹的时, 从图上看,就是整个曲线段在它任一点的切线的上方;当曲线是凸的时, 就是整个曲线段总在它任一点的切线的下方.
从图 4-12 中, 可以看出, 凹的曲线段上连接任两点的弦总位于这两点间的弧段的上方,而凸的曲线段正好相反.
因此,很容易得到如下等价定义:
Definition 4.3.2.
定义 曲线 \(y=f(x)\) 在区间 \(I\) 上是凹的充分必要条件是对 \(I\) 上任意两点 \(x_{1}, x_{2}\text{,}\) 恒有
\begin{equation*}
\frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}>f\left(\frac{x_{1}+x_{2}}{2}\right)
\end{equation*}
曲线 \(y=f(x)\) 在区间 \(I\) 上是凸的充分必要条件是对 \(I\) 上任意两点 \(x_{1}, x_{2}\text{,}\)恒有
\begin{equation*}
\frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}<f\left(\frac{x_{1}+x_{2}}{2}\right)
\end{equation*}
从图 4-12 中还可以看出, 凹的曲线段 ( \(x\) 从 \(x_{1}\) 到 \(x_{2}\) 的一段) 上切线的斜率随 \(x\) 的增长而增大,而切线的斜率是 \(f^{\prime}(x)\text{,}\) 即得到 \(f^{\prime}(x)\) 为单调增加, 从而在该区间上 \(f^{\prime \prime}(x)>0\text{;}\) 凸的曲线段 ( \(x\) 从 \(x_{1}\) 到 \(x_{2}\) 的一段) 的切线的斜率随 \(x\) 的增加而减少, 所以 \(f^{\prime}(x)\) 在该区间内是单调减少的, 从而在该区间上 \(f^{\prime \prime}(x)<0\text{.}\) 且经研究, 这种结论反过来也成立. 因此就有下列利用二阶导数来判定曲线凹凸性的定理.
Theorem 4.3.3.
定理 1 设函数 \(y=f(x)\) 在 \([a, b]\) 上连续,在 \((a, b)\) 内具有二阶导数,那么
- 若在 \((a, b)\) 内 \(f^{\prime \prime}(x)>0\text{,}\) 则 \(y=f(x)\) 在 \([a, b]\) 上这段曲线弧是凹的;
- 若在 \((a, b)\) 内 \(f^{\prime \prime}(x)<0\text{,}\) 则 \(y=f(x)\) 在 \([a, b]\) 上这段曲线弧是凸的.
Proof.
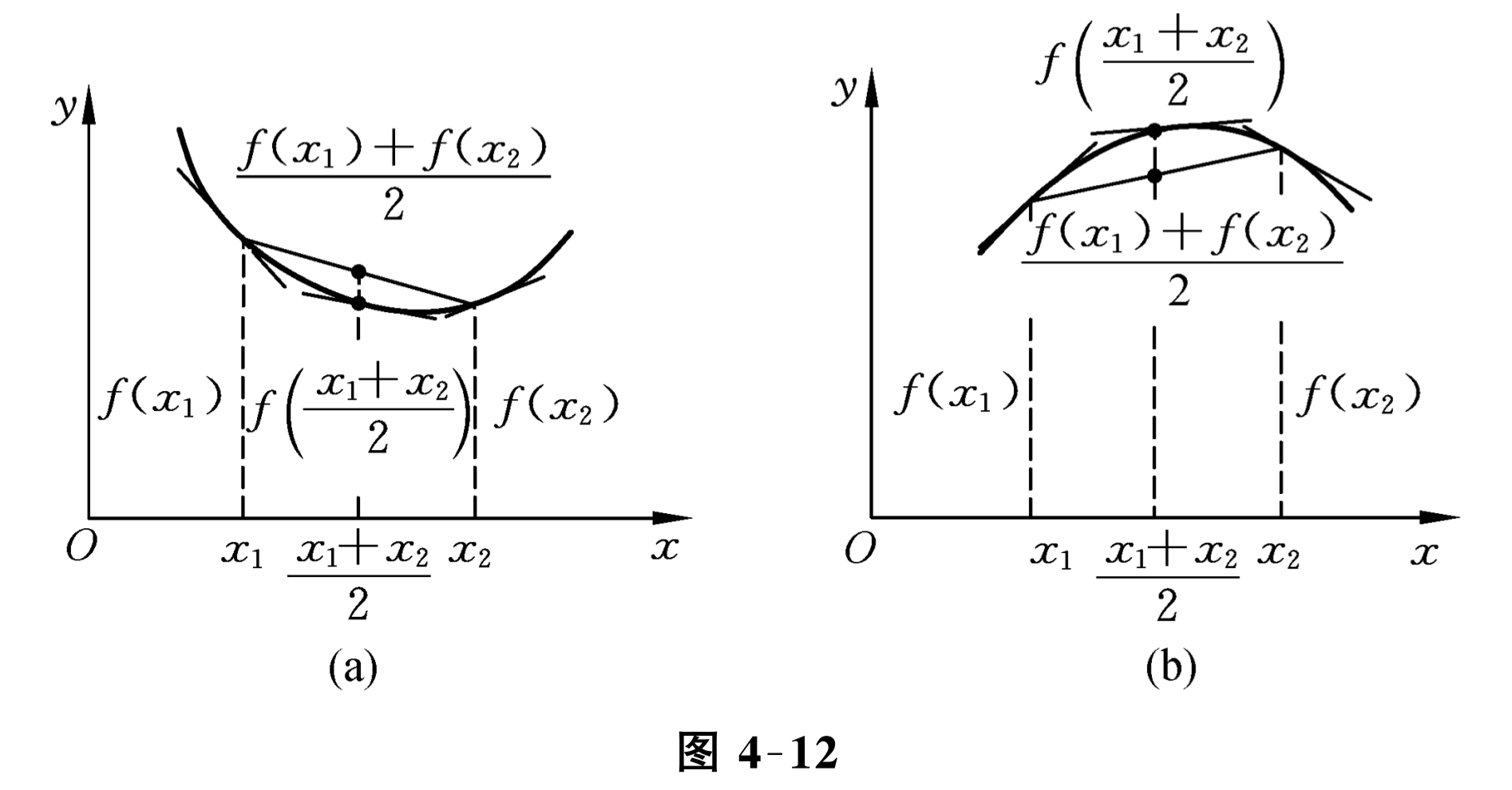
设 \(x_{1}\) 和 \(x_{2}\) 为 \([a, b]\) 上任意两点, 且 \(x_{1}<x_{2}\text{,}\) 记 \(\frac{x_{1}+x_{2}}{2}=x_{0}\text{,}\) 并记 \(x_{2}-x_{0}=\) \(x_{0}-x_{1}=h\text{,}\)则 \(x_{1}=x_{0}-h, x_{2}=x_{0}+h\text{,}\) 由拉格朗日中值公式,得
\begin{equation*}
f\left(x_{0}+h\right)-f\left(x_{0}\right)=f^{\prime}\left(x_{0}+\theta_{1} h\right) h,
\end{equation*}
\begin{equation*}
f\left(x_{0}\right)-f\left(x_{0}-h\right)=f^{\prime}\left(x_{0}-\theta_{2} h\right) h,
\end{equation*}
其中 \(0<\theta_{1}<1,0<\theta_{2}<1\text{.}\) 两式相减, 即得
\begin{equation*}
f\left(x_{0}+h\right)+f\left(x_{0}-h\right)-2 f\left(x_{0}\right)=\left[f^{\prime}\left(x_{0}+\theta_{1} h\right)-f^{\prime}\left(x_{0}-\theta_{2} h\right)\right] h .
\end{equation*}
对 \(f^{\prime}(x)\) 在区间 \(\left[x_{0}-\theta_{2} h, x_{0}+\theta_{1} h\right]\) 上再应用拉格朗日中值公式,得
\begin{equation*}
\left[f^{\prime}\left(x_{0}+\theta_{1} h\right)-f^{\prime}\left(x_{0}-\theta_{2} h\right)\right] h=f^{\prime \prime}(\xi)\left(\theta_{1}+\theta_{2}\right) h^{2},
\end{equation*}
其中 \(x_{0}-\theta_{2} h<\xi<x_{0}+\theta_{1} h\text{.}\) 按Theorem 4.3.3 中(1) 的假设, \(f^{\prime \prime}(\xi)>0\text{,}\) 故有 即
\begin{equation*}
\begin{gathered}
f\left(x_{0}+h\right)+f\left(x_{0}-h\right)-2 f\left(x_{0}\right)>0, \\
\frac{f\left(x_{0}+h\right)+f\left(x_{0}-h\right)}{2}>f\left(x_{0}\right), \\
\frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}>f\left(\frac{x_{1}+x_{2}}{2}\right) .
\end{gathered}
\end{equation*}
于是要寻找 \(f(x)\) 的凹凸区间, 实际上就是找出 \(y^{\prime \prime}\) 的同号区间 (即符号不改变的区间). 像讨论函数单调性时确定 \(y^{\prime}\) 的同号区间那样, 先求出 \(y^{\prime \prime}=0\) 以及 \(y^{\prime \prime}\) 不存在的点, 然后列表定出每个区间内 \(y^{\prime \prime}\) 的符号.
Example 4.3.4.
例 1 判定曲线 \(y=\ln x\) 的凹凸性.
Solution.
解 因为 \(y^{\prime}=\frac{1}{x}, y^{\prime \prime}=-\frac{1}{x^{2}}\text{,}\) 所以在函数的定义域 \((0,+\infty)\) 内 \(y^{\prime \prime}<0\text{.}\) 由 Theorem 4.3.8 得到曲线 \(y=\ln x\) 在 \((0,+\infty)\) 内是凸的.
Example 4.3.5.
例 2 判定曲线 \(y=x^{\frac{1}{3}}\) 的凹凸性.
Solution.
解 当 \(x \neq 0\) 时, \(y^{\prime \prime}=-\frac{2}{9} x^{-\frac{5}{3}}\text{.}\) 所以在 \((-\infty, 0)\) 内 \(y^{\prime \prime}>0\text{,}\) 曲线 \(y=x^{\frac{1}{3}}\) 在 \((-\infty, 0)\) 内是凹的; 在 \((0,+\infty)\) 内 \(y^{\prime \prime}<0\text{,}\) 曲线 \(y=x^{\frac{1}{3}}\) 在 \((0,+\infty)\) 内是凸的.
Example 4.3.6.
例 3 判定曲线 \(y=1+x^{2}+\frac{x^{3}}{3}-x^{4}\) 的凹凸性.
Solution.
解 \(y^{\prime}=2 x+x^{2}-4 x^{3}, y^{\prime \prime}=2+2 x-12 x^{2}=2(1+3 x)(1-2 x)\text{.}\)
令 \(y^{\prime \prime}=0\text{,}\) 得 \(x=-\frac{1}{3}\) 及 \(x=\frac{1}{2}\text{,}\) 列表如下:
Example 4.3.5 中的 \(x=0\) 及Example 4.3.6 中的 \(x=-\frac{1}{3}, x=\frac{1}{2}\) 的两侧, 曲线的凹凸性有所改变. 这种凹凸区间分界点 \(\left(x_{0}, f\left(x_{0}\right)\right)\) 称为曲线的拐点.
Definition 4.3.7.
定义 2 若连续曲线上的点 \(C\) 是曲线凹弧和凸弧的分界点, 则称点 \(C\) 为曲线的拐点.
注意 由拐点定义知, 拐点 \(M_{0}\left(x_{0}, f\left(x_{0}\right)\right)\) 是曲线上的点, 它与极值点的概念不同. 在Example 4.3.5中的点 \((0,0)\) 及Example 4.3.6 中的点 \(\left(-\frac{1}{3},\left.y\right|_{x=-\frac{1}{3}}\right),\left(\frac{1}{2},\left.y\right|_{x=\frac{1}{2}}\right)\) 是曲线的拐点, Example 4.3.4 对应的曲线在整个定义区间上都是凸的，从而没有拐点. 如何寻求曲线 \(y=f(x)\) 的拐点呢? 若 \(f^{\prime \prime}(x)\) 在左右两侧异号, 则点 \(\left(x_{0}, f\left(x_{0}\right)\right)\) 为拐点. 对于二阶可导函数有下述拐点存在的必要条件:
Theorem 4.3.8.
定理 2 设函数 \(y=f(x)\) 二阶可导, 若点 \(\left(x_{0}, y_{0}\right)\) 为 \(y=f(x)\) 的拐点, 则 \(f^{\prime \prime}\left(x_{0}\right)=0\text{.}\)
Proof.
由拐点定义及Theorem 4.3.3 易证得.
Theorem 4.3.8 为寻求拐点指出了范围, 即具有二阶导数 \(f^{\prime \prime}(x)\) 的曲线 \(y=f(x)\text{,}\) 它的拐点的横坐标只需从使 \(f^{\prime \prime}(x)=0\) 成立的点及 \(f^{\prime \prime}(x)\) 不存在的点处去寻找. 通常求拐点的步骤为:
- 求 \(f^{\prime \prime}(x)\text{;}\)
- 令 \(f^{\prime \prime}(x)=0\text{,}\) 解出这个方程在定义域内的实根, 及求出定义域内 \(f^{\prime \prime}(x)\) 不存在的点;
- 对于 (2) 中解出的每个实根和 \(f^{\prime \prime}(x)\) 不存在的点 \(x_{0}\text{,}\) 考虑 \(f^{\prime \prime}(x)\) 在 \(x_{0}\) 的左右两侧邻近点的符号, 若 \(f^{\prime \prime}(x)\) 在 \(x_{0}\) 的左右两侧邻近点的符号相反, 则点 \(\left(x_{0}, f\left(x_{0}\right)\right)\)是拐点; 当两侧邻近点的符号相同时,则点 \(\left(x_{0}, f\left(x_{0}\right)\right)\) 不是拐点.
Example 4.3.9.
例 4 求曲线 \(y=\mathrm{e}^{-x^{2}}\) 的拐点.
Solution.
解 \(y^{\prime}=-2 x \mathrm{e}^{-x^{2}}, y^{\prime \prime}=2\left(2 x^{2}-1\right) \mathrm{e}^{-x^{2}}\text{.}\) 令 \(y^{\prime \prime}=0\text{,}\) 解得 \(x= \pm \frac{1}{\sqrt{2}}\text{.}\)
当 \(x>\frac{1}{\sqrt{2}}\) 或 \(x<-\frac{1}{\sqrt{2}}\) 时, \(y^{\prime \prime}>0\text{;}\) 当 \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\) 时, \(y^{\prime \prime}<0\text{.}\) 因此在 \(\left(-\infty,-\frac{1}{\sqrt{2}}\right)\) 与 \(\left(\frac{1}{\sqrt{2}},+\infty\right)\) 内曲线是凹的; 在区间 \(\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) 内曲线是凸的.从而 \(\left(\frac{1}{\sqrt{2}}, \mathrm{e}^{-\frac{1}{2}}\right)\) 与 \(\left(-\frac{1}{\sqrt{2}}, \mathrm{e}^{-\frac{1}{2}}\right)\) 都是拐点.
Example 4.3.10.
例 5 利用曲线的凹凸性证明不等式: 设 \(a>0, b>0, a \neq b\text{,}\) 则
\begin{equation*}
a^{p}+b^{p}>2^{1-p}(a+b)^{p} \quad(p>1) .
\end{equation*}
Solution.
证 在 \(x>0\) 上考察函数 \(f(x)=x^{p}\text{,}\) 则 \(f^{\prime}(x)=p x^{p-1}, f^{\prime \prime}(x)=p(p-1) x^{p-2}\text{.}\) 当 \(p>1\) 时, \(f^{\prime \prime}(x)>0\) (对任意的 \(x>0\) ), 因此曲线 \(y=f(x)\) 在 \((0,+\infty)\) 内是凹的. 由Theorem 4.3.3 得,对任意的 \(a>0, b>0, a \neq b\text{,}\) 有
\begin{equation*}
\frac{f(a)+f(b)}{2}>f\left(\frac{a+b}{2}\right),
\end{equation*}
即
\begin{equation*}
\frac{1}{2}\left(a^{p}+b^{p}\right)>\left(\frac{a+b}{2}\right)^{p},
\end{equation*}
则
\begin{equation*}
a^{p}+b^{p}>2^{1-p}(a+b)^{p} \quad(p>1) .
\end{equation*}
Subsection 4.3.2 习题
-
判定下列曲线的凹凸性, 并指出其拐点:
- \(y=2 x^{3}-3 x^{2}-36 x+25\text{;}\)
- \(y=x+\frac{1}{x}\text{;}\)
- \(y=\ln \left(x^{2}+1\right)\text{;}\)
- \(y=x^{2}+\frac{1}{x}\text{.}\)
- 问 \(a\) 为何值时,点 \((1,1)\) 是曲线 \(y=x^{3}+a \ln x\) 的拐点?
- 若点 \((1,3)\) 为曲线 \(y=a x^{3}+b x^{2}\) 的拐点, 问 \(a, b\) 应取何值?
-
利用曲线的凹凸性证明不等式:
- \(2 \cos \frac{x+y}{2}>\cos x+\cos y,(x, y) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\text{;}\)
- \((x+y) \ln \frac{x+y}{2}<x \ln x+y \ln y, 0<x<y\text{;}\)
- \(\mathrm{e}^{\frac{x+y}{2}}<\frac{\mathrm{e}^{x}+\mathrm{e}^{y}}{2}\text{.}\)
- 证明曲线 \(y=\frac{x+1}{x^{2}+1}\) 有三个拐点在同一直线上.
