Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 3.1 微分学三个基本定理

对一条在各点处都有非铅直切线的曲线弧 \(y=\) \(f(x), x \in[a, b]\text{,}\) 若它的两个端点有相同的纵坐标,那么在这条曲线上至少有一点的切线是水平的, 即该切线平行于曲线弧的两端点的连线 \(\overline{A B}\text{,}\) 图 3-1 中的 \(P_{1}, P_{2}, P_{3}, P_{4}, P_{5}\) 点处的切线平行于 \(\overline{A B}\) 弦, 这是一个明显的几何事实. 下面将证明这个从几何直观上得出的结论. 先介绍一个引理.

Subsection 3.1.1 费马 (Fermat)引理

Proof.

证 这里仅就 \(f\left(x_{0}\right)\) 为最大的情形来证明,读 者可以自己证明 \(f\left(x_{0}\right)\) 为最小时的情形.
\(y=f(x)\) 在 \(x_{0}\) 处可导, 即极限
\begin{equation*} f^{\prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \end{equation*}
存在,所以按 \(f(x)\) 在 \(x_{0}\) 处可导的充分必要条件有
\begin{equation*} \lim\limits_{x \rightarrow x_{0}^{-}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}=f^{\prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}^{+}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} . \end{equation*}
当 \(x\) 接近 \(x_{0}\) 时, 必定存在 \(x_{0}\) 的某个邻域 \(U\left(x_{0}\right)\text{,}\) 在 \(U\left(x_{0}\right)\) 内 \(f\left(x_{0}\right)\) 最大, 即有
\begin{equation*} f(x) \leqslant f\left(x_{0}\right) \text { 或 } f(x)-f\left(x_{0}\right) \leqslant 0, x \in U\left(x_{0}\right) \text {. } \end{equation*}
于是对任意 \(x \in \dot{U}\left(x_{0}\right)\text{,}\) 当 \(x-x_{0}<0\) 时,有 \(\frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \geqslant 0\text{,}\) 从而
\begin{equation*} f^{\prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}^{-}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \geqslant 0 \end{equation*}
当 \(x-x_{0}>0\) 时,有 \(\frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \leqslant 0\text{,}\) 从而
所以
\begin{equation*} f^{\prime}\left(x_{0}\right)=\lim\limits_{x \rightarrow x_{0}^{+}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}} \leqslant 0 \end{equation*}
\begin{equation*} f^{\prime}\left(x_{0}\right)=0 \text {. } \end{equation*}
引理有一个简明的几何解释: 如果曲线 \(y=\) \(f(x)\) 上某一点的纵坐标比它左右邻近点的纵坐标小 (或大), 且曲线在这点又有非铅直的切线, 那么这条切线一定是水平的 (即平行于 \(x\) 轴), 如图 3-2 中的过点 \(P, Q\) 的切线.
由费马引理可以得出一个非常有用的定理.

Subsection 3.1.2 罗尔定理

Proof.

证 因为函数 \(y=f(x)\) 在闭区间 \([a, b]\) 上连续, 所以它在 \([a, b]\) 上必能取到最 大值 \(M\) 与最小值 \(m\text{.}\) 如果 \(M=m\text{,}\) 那么 \(f(x)\) 在 \([a, b]\) 上是一个常数, \(f^{\prime}(x)\) 在 \((a, b)\)内每个点都为零. 这时区间 \((a, b)\) 内任一点都可以作为定理结论中的 \(\xi\text{,}\) 从而结论成立.
如果 \(M>m\text{,}\) 那么 \(M\) 与 \(m\) 这两个不同的数值中至少有一个与 \(f(a)=f(b)\) 不相等, 设 \(M \neq f(a)=f(b)\text{,}\) 那么这个最大值 \(M\) 必定是在区间 \((a, b)\) 内部的某点达到, 这就是说, 区间 \((a, b)\) 内至少存在一个点 \(\xi\text{,}\) 使 \(f(\xi)=M\text{.}\) 于是对一切 \(x \in[a, b]\) 有 \(f(x) \leqslant f(\xi)=M\text{,}\) 但 \(\xi\) 是 \((a, b)\) 内部的点, 因此, 存在 \(\xi\) 点的邻域 \(U(\xi) \subset(a, b)\text{,}\) 对 \(U(\xi)\)内的一切点 \(x\) 有 \(f(x) \leqslant f(\xi)\text{.}\) 又因 \(f(x)\) 在 \((a, b)\) 内可导,所以 \(f(x)\) 在 \(\xi\) 处可导, 由费马引理知
\begin{equation*} f^{\prime}(\xi)=0 \end{equation*}
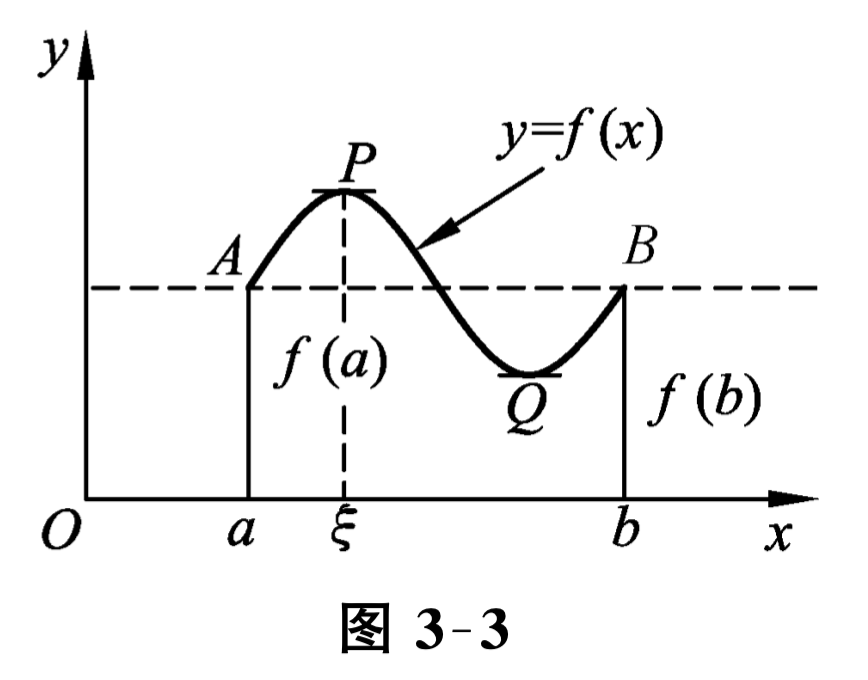
罗尔定理的几何解释是: 在一段两个端点处纵坐标相等的连续曲线弧上, 若除两端点外各点处都有非铅直的切线,那么这些切线中至少有一条是水平的,如图 3-3 中点 \(P, Q\) 处的切线平行于 \(x\) 轴. 也就是说, 至少存在一条切线平行于曲线两端点的弦 \(\overline{A B}\text{.}\)
注意 罗尔定理中的条件是充分条件而非必要条件, 即当满足定理的条件时, 结论一定成立; 若不满足定理的条件,结论可能成立也可能不成立. 罗尔定理肯定了在 \((a, b)\) 内至少存在一点 \(\xi\text{,}\) 使 \(f^{\prime}(\xi)=0\text{.}\) 尽管没有指出 \(\xi\) 的确切值,但它在实际应用中非常重要.

Example 3.1.3.

例 1 验证罗尔定理对函数 \(f(x)=x^{2}-5 x+4\) 在区间 \([2,3]\) 上的正确性.
Solution.
解 \(f(x)=x^{2}-5 x+4\) 是一个多项式函数,显然它在 \((-\infty,+\infty)\) 内连续、可导,且 \(f(2)=f(3)=-2\text{,}\) 所以 \(f(x)=x^{2}-5 x+4\) 在区间 \([2,3]\) 上满足罗尔定理的全部条件,因此可以断定必定存在 \(\xi \in(2,3)\text{,}\) 使得 \(f^{\prime}(\xi)=0\text{.}\) 实际上由 \(f^{\prime}(x)=\) \(2 x-5=0\) 可知 \(\xi=\frac{5}{2} \in(2,3)\text{,}\) 确有 \(f^{\prime}(\xi)=0\text{.}\)

Example 3.1.4.

例 2 不用求出函数 \(f(x)=(x+1)(x-1)(x-2)(x-3)\) 的导数, 应用罗尔定理, 说明方程 \(f^{\prime}(x)=0\) 有几个实根,并指出它们所在区间.
Solution.
解 因为函数 \(f(x)\) 在 \([-1,1]\) 上满足罗尔定理的条件, 故至少存在一点 \(\xi_{1} \in\) \((-1,1)\text{,}\) 使得
\begin{equation*} f^{\prime}\left(\xi_{1}\right)=0 \end{equation*}
同样可证, 在区间 \((1,2)\) 与 \((2,3)\) 内分别至少存在一点 \(\xi_{2} \in(1,2)\) 与 \(\xi_{3} \in(2,3)\text{,}\)使得
\begin{equation*} f^{\prime}\left(\xi_{2}\right)=0, f^{\prime}\left(\xi_{3}\right)=0 . \end{equation*}
由于 \(f(x)\) 是 \(x\) 的四次函数,故 \(f^{\prime}(x)\) 是 \(x\) 的三次函数，因此 \(f^{\prime}(x)=0\) 是 \(x\) 的三次代数方程, 它至多有三个实根. 已证明它确实有三个实根, 且分别位于区间 \((-1,1),(1,2),(2,3)\) 内.

Example 3.1.5.

例 3 证明二阶可导的函数 \(y=f(x)\) 的三个相异的零点之间至少有一个二阶导数 \(f^{\prime \prime}(x)\) 的零点.
Solution.
证 设 \(x_{1}<x_{2}<x_{3}\) 是 \(y=f(x)\) 的三个零点,即
\begin{equation*} f\left(x_{1}\right)=f\left(x_{2}\right)=f\left(x_{3}\right)=0 . \end{equation*}
对函数 \(y=f(x)\) 在区间 \(\left[x_{1}, x_{2}\right]\) 上应用罗尔定理,则存在 \(\xi_{1} \in\left(x_{1}, x_{2}\right)\) ，使
\begin{equation*} f^{\prime}\left(\xi_{1}\right)=0 \text {. } \end{equation*}
在区间 \(\left[x_{2}, x_{3}\right]\) 上应用罗尔定理,则存在 \(\xi_{2} \in\left(x_{2}, x_{3}\right)\) ，使
\begin{equation*} f^{\prime}\left(\xi_{2}\right)=0 \end{equation*}
再对函数 \(y^{\prime}=f^{\prime}(x)\) 在区间 \(\left[\xi_{1}, \xi_{2}\right]\) 上应用罗尔定理,则至少存在 \(\xi \in\left(\xi_{1}, \xi_{2}\right) \subset\) \(\left[x_{1}, x_{3}\right]\text{,}\) 使 \(f^{\prime \prime}(\xi)=0\text{.}\)

Subsection 3.1.3 拉格朗日中值定理

在罗尔定理中,函数 \(y=f(x)\) 在闭区间 \([a, b]\) 上满足罗尔定理三条件,则曲线 \(y=f(x)\) 必存在平行于弦 \(\overline{A B}\) 的切线 (见图 3-3), 但若罗尔定理的第三个条件不满足, 即 \(f(a) \neq f(b)\text{,}\) 这时是否能在曲线 \(y=f(x)\) 上找到一点, 使得曲线在该点的切线仍平行于曲线两端点的弦 \(\overline{A B}\) 呢?
由于弦 \(\overline{A B}\) 的斜率等于 \(\frac{f(b)-f(a)}{b-a}\text{,}\)而 \(f^{\prime}(x)\) 表示曲线 \(y=f(x)\) 上横坐标为 \(x\)的点处的切线的斜率, 因此上面的问题又可叙述为: 在开区间 \((a, b)\) 内能否找到一点 \(\xi\text{,}\) 使得
\begin{equation*} f^{\prime}(\xi)=\frac{f(b)-f(a)}{b-a} \end{equation*}
或
\begin{equation*} f(b)-f(a)=f^{\prime}(\xi)(b-a) . \end{equation*}
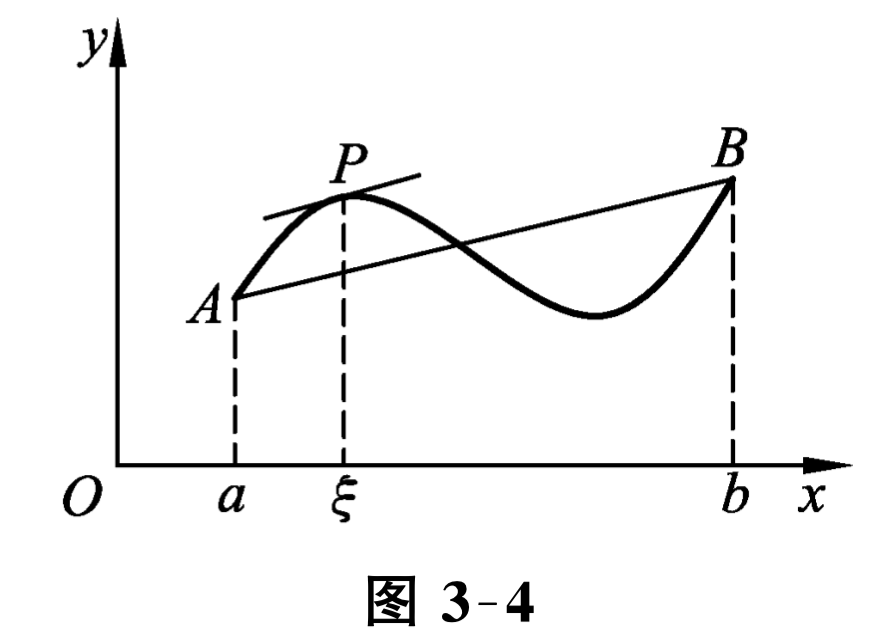
从图 3-4 可以明显看到,这样的点 \(\xi\) 是存在的,于是我们又得到一个很重要的定理.

Proof.

证 注意到: 曲线的方程是 \(y=f(x), x \in[a, b]\text{,}\) 弦 \(\overline{A B}\) 的方程是
\begin{equation*} \bar{y}-f(a)=\frac{f(b)-f(a)}{b-a}(x-a) \end{equation*}
作函数 \(F(x)=y-\bar{y}=f(x)-\left[f(a)+\frac{f(b)-f(a)}{b-a}(x-a)\right]\text{,}\) 它是曲线 \(f(x)\)和弦 \(\overline{A B}\) 的差. 它们显然在 \([a, b]\) 上连续, 在 \((a, b)\) 内可导, 且 \(F(a)=F(b)=0\text{,}\) 所以 \(F(x)\) 在 \([a, b]\) 上满足罗尔定理Theorem 3.1.2的条件. 于是推出必存在 \(\xi \in(a, b)\) 使 \(F^{\prime}(\xi)=0\text{.}\) 即证明了 \(f^{\prime}(\xi)=\frac{f(b)-f(a)}{b-a}\text{.}\)
显然 \(f(a)=f(b)\) 时, 拉格朗日中值定理就转化成罗尔定理, 因此罗尔定理是拉格朗日中值定理的特殊情形,而拉格朗日中值定理是罗尔定理的推广. 拉格朗日中值定理的几何解释是:一段连接点 \((a, f(a))\) 与点 \((b, f(b))\) 的连续曲线弧上, 除两端点外如果都有非铅直的切线, 那么这些切线中至少有一条是与连接这两端点的弦相平行的. 如图 3-4 中的点 \(P\) 处的切线. 公式
\begin{equation*} f(b)-f(a)=f^{\prime}(\xi)(b-a) \quad(a<\xi<b) \end{equation*}
称为微分中值公式或拉格朗日中值公式. 若 \(b<a\text{,}\) 而 \(f(x)\) 在 \([b, a]\) 上连续, 在 \((b\text{,}\) a) 内可导,则相应有
\begin{equation*} f(a)-f(b)=f^{\prime}(\xi)(a-b) \quad(b<\xi<a) . \end{equation*}
因此, 不论 \(a<b\text{,}\) 还是 \(b<a\text{,}\) 可以将微分中值公式写成
\begin{equation*} f(b)-f(a)=f^{\prime}(\xi)(b-a)(\xi \text { 在 } a \text { 与 } b \text { 之间 }) . \end{equation*}
由于 \(\xi\) 在 \(a\) 与 \(b\) 之间, 所以也可以写成 \(\xi=a+\theta(b-a) \quad(0<\theta<1)\text{,}\) 即
\begin{equation*} f(b)-f(a)=f^{\prime}[a+\theta(b-a)](b-a) \quad(0<\theta<1) . \end{equation*}
如果函数 \(y=f(x)\) 在以 \(x, x+\Delta x\) 为端点的区间上满足拉格朗日定理的条件, 那么就有
\begin{equation*} \Delta y=f(x+\Delta x)-f(x)=f^{\prime}(x+\theta \Delta x) \cdot \Delta x \quad(0<\theta<1) . \end{equation*}
这个公式称为有限增量公式, 它准确地表达了函数在一个区间上的增量与函数在区间内某点处的导数之间的关系.
证 对于 \((a, b)\) 内任意两点 \(x_{1}, x_{2}\text{,}\) 不妨设 \(x_{1}<x_{2}\text{,}\) 则 \(\left[x_{1}, x_{2}\right] \subset(a, b)\text{,}\) 所以 \(f(x)\) 在 \(\left[x_{1}, x_{2}\right]\) 上连续, 在 \(\left(x_{1}, x_{2}\right)\) 内可导. 由拉格朗日中值定理有
\begin{equation*} f\left(x_{2}\right)-f\left(x_{1}\right)=f^{\prime}(\xi)\left(x_{2}-x_{1}\right) \quad\left(x_{1}<\xi<x_{2}\right) . \end{equation*}
因为 \(\xi \in\left(x_{1}, x_{2}\right) \subset(a, b)\text{,}\) 而 \((a, b)\) 内每一点 \(x\) 处 \(f^{\prime}(x)=0\text{,}\) 所以 \(f^{\prime}(\xi)=0\text{,}\)于是得 \(f\left(x_{2}\right)-f\left(x_{1}\right)=0\text{,}\) 即 \(f\left(x_{2}\right)=f\left(x_{1}\right)\text{.}\) 既然对于 \((a, b)\) 内任意两点 \(x_{1}, x_{2}\)都有 \(f\left(x_{2}\right)=f\left(x_{1}\right)\text{,}\) 这就说明 \(f(x)\) 在 \((a, b)\) 内是一个常数. Corollary 3.1.7 中的区间 \((a, b)\) 可换成 \([a, b],(a,+\infty),[a, b),(-\infty,+\infty)\) 等任何 区间. 由导数知识知道 “常数函数的导数恒等于零”, Corollary 3.1.7 说明它的逆命题也是成立的.
证 因为在 \((a, b)\) 内每一点 \(x\) 处都有 \([f(x)-g(x)]^{\prime}=f^{\prime}(x)-g^{\prime}(x)=0\text{,}\) 所以由Corollary 3.1.7 知 \(f(x)-g(x)\) 在 \((a, b)\) 内是一个常数, 记作 \(C\text{,}\) 即
\begin{equation*} f(x)-g(x)=C, x \in(a, b), \end{equation*}
于是
\begin{equation*} f(x)=g(x)+C, x \in(a, b) . \end{equation*}
我们知道“两个函数恒等,那么它们的导数相等”, 由Corollary 3.1.8 得到 “两个函数的导数恒等,那么它们至多相差一个常数”. 这个结论在积分学中经常用到.

Example 3.1.9.

例 4 证明不等式: \(|\arctan a-\arctan b| \leqslant|a-b|\text{.}\)
Solution.
证 设函数 \(f(x)=\arctan x\text{,}\)则 \(f(x)\) 在 \((-\infty,+\infty)\) 内处处连续,处处可导.所以在以 \(a\) 和 \(b\) 为端点的区间上,函数 \(f(x)\) 满足拉格朗日中值定理的条件,从而
\begin{equation*} \arctan a-\arctan b=\left.(\arctan x)^{\prime}\right|_{x=\xi}(a-b) \quad(\xi \text { 在 } a \text { 与 } b \text { 之间 }), \end{equation*}
即
\begin{equation*} \arctan a-\arctan b=\frac{a-b}{1+\xi^{2}} \end{equation*}
因为 \(\frac{1}{1+\xi^{2}} \leqslant 1\text{,}\) 从而
\begin{equation*} |\arctan a-\arctan b|=\frac{|a-b|}{1+\xi^{2}} \leqslant|a-b| \end{equation*}

Example 3.1.10.

例 5 证明恒等式:
\begin{equation*} \arcsin x+\arccos x=\frac{\pi}{2} \quad(-1 \leqslant x \leqslant 1) . \end{equation*}
Solution.
证 设 \(f(x)=\arcsin x+\arccos x\text{,}\) 则 \(f^{\prime}(x)=\frac{1}{\sqrt{1-x^{2}}}-\frac{1}{\sqrt{1-x^{2}}}=0\text{,}\) 从而推出在 \((-1,1)\) 上, \(f(x) \equiv C\) (常数).
又因为 \(f(0)=f(-1)=f(1)=\frac{\pi}{2}\text{,}\) 所以 \(f(x)=\frac{\pi}{2}\text{,}\) 即
\begin{equation*} \arcsin x+\arccos x=\frac{\pi}{2} \quad(-1 \leqslant x \leqslant 1) . \end{equation*}

Example 3.1.11.

例 6 已知函数 \(f(x)\) 在闭区间 \([0, c]\) 上有单调减少的导数 \(f^{\prime}(x)\text{,}\) 并且 \(f(0)=0\text{,}\)证明对于满足 \(0<a<b<a+b<c\) 的任何 \(a, b\text{,}\) 总有 \(f(a)+f(b)>f(a+b)\text{.}\)
Solution.
证 对函数 \(f(x)\) 在 \([0, a]\) 上应用拉格朗日定理,得
\begin{equation*} f(a)=f(a)-f(0)=f^{\prime}\left(\xi_{1}\right) \cdot a \quad\left(0<\xi_{1}<a\right) ; \end{equation*}
再在 \([b, a+b]\) 上应用拉格朗日定理,得
\begin{equation*} f(a+b)-f(b)=f^{\prime}\left(\xi_{2}\right) \cdot a \quad\left(b<\xi_{2}<a+b\right) . \end{equation*}
因为 \(f^{\prime}(x)\) 在 \([0, c]\) 上单调减少, 而 \(0<\xi_{1}<a<b<\xi_{2}<a+b<c\text{,}\) 因此
\begin{equation*} f^{\prime}\left(\xi_{2}\right)<f^{\prime}\left(\xi_{1}\right), \end{equation*}
从而
\begin{equation*} f(a+b)-f(b)-f(a)=\left[f^{\prime}\left(\xi_{2}\right)-f^{\prime}\left(\xi_{1}\right)\right] \cdot a<0, \end{equation*}
亦即
\begin{equation*} f(a)+f(b)>f(a+b) . \end{equation*}

Subsection 3.1.4 柯西定理

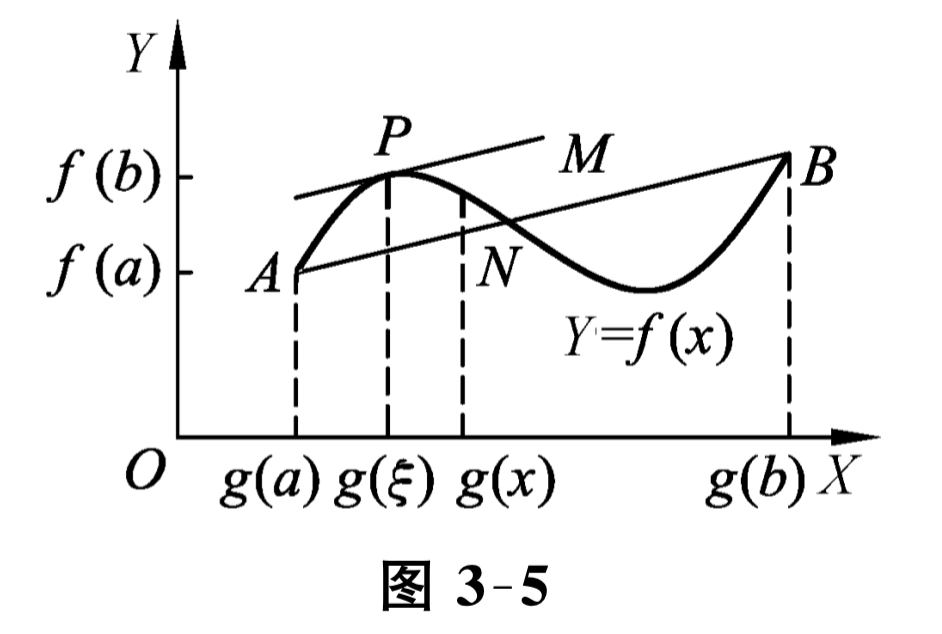
在上述拉格朗日中值定理中, 如果曲线 \(\overparen{A B}\) 由参数方程
\begin{equation*} \left\{\begin{array}{l} X=g(x), \quad(a \leqslant x \leqslant b) \\ Y=f(x) \end{array}\right. \end{equation*}
表示 (见图 3-5), 其中 \(x\) 为参数, 那么曲线上点 \((X, Y)\) 处的切线斜率为
\begin{equation*} \frac{\mathrm{d} Y}{\mathrm{~d} X}=\frac{f^{\prime}(x)}{g^{\prime}(x)} \end{equation*}
弦 \(\overline{A B}\) 的斜率为
\begin{equation*} \frac{f(b)-f(a)}{g(b)-g(a)} \end{equation*}
假定点 \(P\) 对应于参数 \(x=\xi\text{,}\) 那么曲线上点 \(P\) 处的切线平行于弦 \(\overline{A B}\text{,}\) 可表示为
\begin{equation*} \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime}(\xi)}{g^{\prime}(\xi)} \end{equation*}
与这一事实相应的是：

Proof.

证 要证明存在 \(\xi \in(a, b)\text{,}\) 使 \(f^{\prime}(\xi)[g(b)-g(a)]=g^{\prime}(\xi)[f(b)-f(a)]\) 成立, 只要证明存在 \(\xi \in(a, b)\text{,}\) 使
\begin{equation*} \left.\{f(x)[g(b)-g(a)]-g(x)[f(b)-f(a)]\}^{\prime}\right|_{x=\xi}=0 . \end{equation*}
为此令 \(\varphi(x)=f(x)[g(b)-g(a)]-g(x)[f(b)-f(a)]\text{,}\) 则不难验证 \(\varphi(x)\) 在 \([a, b]\) 上连续,在 \((a, b)\) 内可导, 且 \(\varphi(b)=\varphi(a)\text{,}\) 由罗尔定理知, 至少存在 \(\xi \in(a, b)\text{,}\)使
\begin{equation*} \varphi^{\prime}(\xi)=0 \end{equation*}
因为 \(\varphi^{\prime}(x)=f^{\prime}(x)[g(b)-g(a)]-g^{\prime}(x)[f(b)-f(a)]\text{,}\) 所以存在 \(\xi \in(a\text{,}\) b), 使
\begin{equation*} f^{\prime}(\xi)[g(b)-g(a)]=g^{\prime}(\xi)[f(b)-f(a)] . \end{equation*}
如果柯西定理中的函数 \(g(x)\) 进一步满足条件: \(g^{\prime}(x) \neq 0, x \in(a, b)\text{,}\) 那么由罗尔定理可知必有 \(g(b) \neq g(a)\text{,}\) 从而柯西定理的结论也可以进一步写成
\begin{equation*} \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime}(\xi)}{g^{\prime}(\xi)} \end{equation*}
\(\xi\) 介于 \(a, b\) 之间.

Example 3.1.13.

例 7 已知 \(\varphi(x)\) 在 \([0,1]\) 上连续,在 \((0,1)\) 内可导, 证明在 \((0,1)\) 内存在 \(\xi\text{,}\) 使
\begin{equation*} \varphi^{\prime}(\xi)=2 \xi[\varphi(1)-\varphi(0)] . \end{equation*}
Solution.
证 要证明存在 \(\xi \in(0,1)\text{,}\) 使 \(\varphi^{\prime}(\xi)=2 \xi[\varphi(1)-\varphi(0)]\text{,}\) 也就是要证明存在 \(\xi \in(0,1)\text{,}\) 使 \(\varphi^{\prime}(\xi)\left(1^{2}-0^{2}\right)=2 \xi[\varphi(1)-\varphi(0)]\text{,}\) 也就是要证明存在 \(\xi \in(0,1)\text{,}\) 使 \(\frac{\varphi^{\prime}(\xi)}{2 \xi}=\frac{\varphi(1)-\varphi(0)}{1^{2}-0^{2}}\text{.}\) 为此取 \(f(x)=\varphi(x), g(x)=x^{2}\text{,}\) 在 \([0,1]\) 上用柯西定理,得
\begin{equation*} \varphi^{\prime}(\xi)=2 \xi[\varphi(1)-\varphi(0)], \xi \in(0,1) . \end{equation*}

Subsection 3.1.5 练习题

  1. 验证罗尔定理对函数 \(f(x)=x^{3}+4 x^{2}-7 x-10\) 在闭区间 \([-1,2]\) 上的正确性.
    1. 验证拉格朗日定理对函数 \(f(x)=\ln x\) 在闭区间 \([1, \mathrm{e}]\) 上的正确性;
    2. 验证拉格朗日定理对函数 \(f(x)=\arctan x\) 在闭区间 \([0,1]\) 上的正确性.
  3. 应用罗尔定理证明: 方程 \(x^{3}-3 x+c=0\) 在闭区间 \([0,1]\) 内不可能有两个不同的实根,其中 \(c\) 为任意实数.
  4. 设函数 \(f(x)\) 在区间 \([1,2]\) 上有二阶导数, 且 \(f(2)=f(1)=0\text{,}\) 又 \(F(x)=(x-1)^{2} f(x)\text{,}\)则在区间 \((1,2)\) 内至少有一点 \(\xi\text{,}\) 使得 \(F^{\prime \prime}(\xi)=0\text{.}\)
  5. 设对于所有的实数对 \(x, y\text{,}\) 不等式 \(|f(y)-f(x)| \leqslant M|y-x|^{2}\) ( \(M\) 为正常数) 都成立, 证明: 在 \(-\infty<x<+\infty\) 上, \(f(x) \equiv\) 常数.
  6. 若实系数多项式
    \begin{equation*} p_{n}(x)=a_{0} x^{n}+a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n} \quad\left(a_{0} \neq 0\right) \end{equation*}
    的根全是实根, 则其各阶导数 \(p_{n}^{\prime}(x), p^{\prime \prime}{ }_{n}(x), \cdots, p_{n}^{(n-1)}(x)\) 也仅有实根, 试证明.
  7. 应用拉格朗日中值定理证明下列不等式:
    1. 当 \(a>b>0, n>1\) 时, \(n b^{n-1}(a-b)<a^{n}-b^{n}<n a^{n-1}(a-b)\text{;}\)
    2. 当 \(x \neq 0\) 时, \(\mathrm{e}^{x}>1+x\text{;}\)
    3. 当 \(0<b \leqslant a\) 时, \(\frac{a-b}{a} \leqslant \ln \frac{a}{b} \leqslant \frac{a-b}{b}\text{;}\)
    4. 当 \(0<a<b\) 时, \((a+b) \ln \frac{a+b}{2}<a \ln a+b \ln b\text{.}\)
  8. 证明下列恒等式:
    1. \(\arctan x=\arcsin \frac{x}{\sqrt{1+x^{2}}}\text{;}\)
    2. 当 \(|x| \leqslant \frac{1}{2}\) 时, \(3 \arccos x-\arccos \left(3 x-4 x^{3}\right)=\pi\text{.}\)
  9. 设 \(f(x), g(x)\) 均为可微函数, \(f(0)=g(0)\text{,}\) 且当 \(x>0\) 时, 有 \(f^{\prime}(x)>g^{\prime}(x)\text{,}\) 试证当 \(x>0\)时, 恒有 \(f(x)>g(x)\text{.}\)
  10. 已知函数 \(f(x)\) 在 \([a, b]\) 上连续, 在 \((a, b)\) 内二阶可导, 连接点 \(A(a, f(a))\text{,}\) 点 \(B(b, f(b))\) 的直线段与曲线弧 \(\widehat{A B}\) 相交于 \(C(c, f(c)), c \in(a, b)\text{,}\) 证明在 \((a, b)\) 内至少存在一点 \(\xi\text{,}\) 使 \(f^{\prime \prime}(\xi)=0\text{.}\)
  11. 已知 \(x_{1} x_{2}>0\text{,}\) 证明在 \(x_{1}, x_{2}\) 之间存在 \(\xi\) 使
    \begin{equation*} x_{1} \mathrm{e}^{x_{2}}-x_{2} \mathrm{e}^{x_{1}}=(1-\xi) \mathrm{e}^{\xi}\left(x_{1}-x_{2}\right). \end{equation*}
  12. 证明方程
    \begin{equation*} x^{n}+a_{1} x^{n-1}+a_{2} x^{n-2}+\cdots+a_{n-1} x-a_{n}=0 \end{equation*}
    (其中 \(a_{i} \geqslant 0, i=1,2, \cdots, n-1, a_{n}>0\) ) 有且仅有一个正根.
PrevTopNext