Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 6.3 微积分基本定理

在建立定积分概念以后, 如何计算定积分就是一个亟待解决的问题. 因为不可能都按定积分的定义用分割、近似、作和、求极限的方法来计算定积分. 由 6.1.1 Subsubsection 6.1.1.2 得出物体以变速 \(v=v(t)\) 在时间间隔 \(\left[T_{1}, T_{2}\right]\) 内走过的路程为
\begin{equation} s=\displaystyle \int_{T_{1}}^{T_{2}} v(t) \mathrm{d} t\tag{6.3.1} \end{equation}
但在不定积分中已知若 \(v=v(t)\)能找出它的原函数: \(s=s(t)=\displaystyle \int v(t) \mathrm{d} t\text{,}\) 则物体由时刻 \(T_{1}\) 到时刻 \(T_{2}\) 走过的路程即为
\begin{equation} s=s\left(T_{2}\right)-s\left(T_{1}\right) .\tag{6.3.2} \end{equation}
比较(6.3.1) 和(6.3.2) , 就得到: \(\displaystyle \int_{T_{1}}^{T_{2}} v(t) \mathrm{d} t=s\left(T_{2}\right)-s\left(T_{1}\right)\text{.}\) 这结果显示出, 被积函数 \(v=v(t)\) 在区间 \(\left[T_{1}, T_{2}\right]\) 上的定积分等于 \(v(t)\) 的原函数 \(s(t)\) 在 \(T_{2}\) 和 \(T_{1}\) 处的函数值的差值: \(s\left(T_{2}\right)-s\left(T_{1}\right)\text{.}\) 这一结论是否具有普遍意义呢? 即若已知 \(F(x)\) 是 \(f(x)\) 的一个原函数, 是否有 \(\displaystyle \int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a)\text{.}\) 为了回答这一问题, 首先研究可变上限的定积分概念.

Subsection 6.3.1 积分上限的函数及其导数

设函数 \(f(x)\) 在区间 \([a, b]\) 上连续, 定积分 \(\displaystyle \int_{a}^{b} f(x) \mathrm{d} x\) 是一个确定的数, 它只与被积函数 \(f(x)\) 和积分的上、下限 \(a, b\) 有关,而与积分变量 \(x\) 的记号无关. 设 \(x\) 为 \([a, b]\) 上一点, 考察 \(f(x)\) 在部分区间 \([a, x]\) 上的定积分 \(\displaystyle \int_{a}^{x} f(x) \mathrm{d} x\text{.}\) 式中积分变量和积分上限都用 \(x\) 表示, 但它们的含义不同. 为了区别它们, 常将积分变量改用 \(t\)表示, 即 \(\displaystyle \int_{a}^{x} f(t) \mathrm{d} t\text{.}\) 由于被积函数 \(f(x)\) 在 \([a, b]\) 上连续, 因此这个定积分存在且随 \(x \in[a, b]\) 的变化而变化,即对任意 \(x \in[a, b]\text{,}\)定积分 \(\displaystyle \int_{a}^{x} f(t) \mathrm{d} t\) 都对应唯一确定的值. 按照函数的定义, 它是定义在区间 \([a, b]\) 上关于积分上限 \(x\) 的函数, 记为 \(\Phi(x)=\displaystyle \int_{a}^{x} f(t) \mathrm{d} t, a \leqslant x \leqslant b\text{.}\) 由于它的自变量 \(x\) 是积分上限, 所以称 \(\Phi(x)\) 为积分上限的函数 (或变上限的定积分). 例如 \(\displaystyle \int_{0}^{x}\left(t^{2}+1\right) \mathrm{d} t, 0 \leqslant x \leqslant 1\text{,}\) 就是定义在区间 \([0,1]\) 上的一个积分上限的函数. 积分上限的函数 \(\Phi(x)\) 的几何意义是: 若 \(f(x) \geqslant 0\text{,}\)对 \([a, b]\) 上任意的 \(x\) 都对应唯一的一个曲边梯形的面积 \(\Phi(x)\text{.}\) 关于这个函数 \(\Phi(x)\) 具有下面重要性质.

Proof.

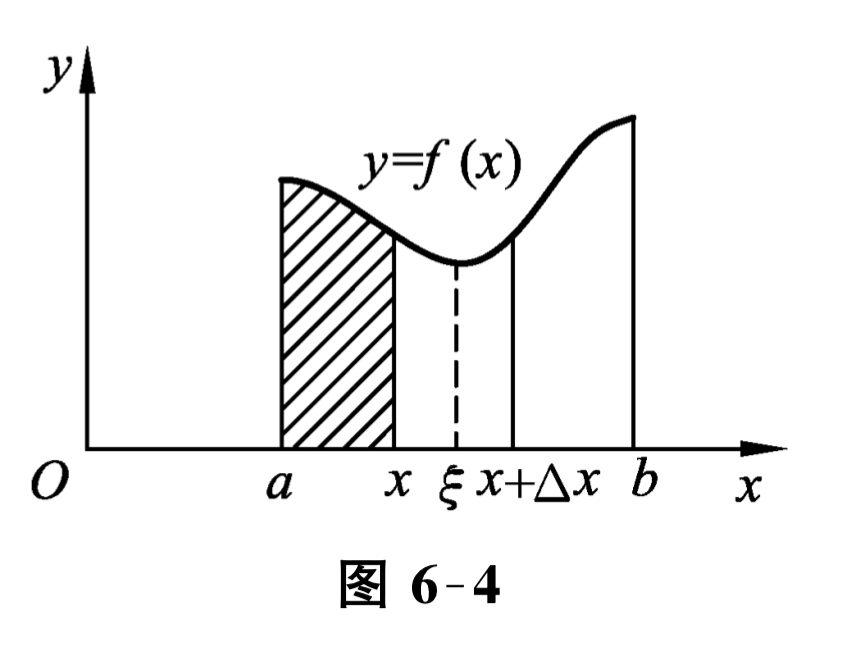
证 如图 6-4 所示,对任意 \(x \in(a, b)\text{,}\) 设 \(x\) 获得增量 \(\Delta x\text{,}\) 让 \(|\Delta x|\) 足够小,使 \(x+\Delta x \in(a, b)\text{,}\) 则
\begin{equation*} \begin{aligned} \Delta \Phi(x) & =\Phi(x+\Delta x)-\Phi(x)=\displaystyle \int_{a}^{x+\Delta x} f(t) \mathrm{d} t-\displaystyle \int_{a}^{x} f(t) \mathrm{d} t \\ & =\displaystyle \int_{a}^{x} f(t) \mathrm{d} t+\displaystyle \int_{x}^{x+\Delta x} f(t) \mathrm{d} t-\displaystyle \int_{a}^{x} f(t) \mathrm{d} t=\displaystyle \int_{x}^{x+\Delta x} f(t) \mathrm{d} t . \end{aligned} \end{equation*}
由积分中值定理得到 \(\displaystyle \int_{x}^{x+\Delta x} f(t) \mathrm{d} t=f(\xi) \Delta x\text{,}\) 所以 \(\Delta \Phi(x)=f(\xi) \Delta x\text{,}\)其中 \(\xi\) 在 \(x\) 与 \(x+\Delta x\) 之间, 把上式两端各除以 \(\Delta x\text{,}\) 得函数增量与自变量增量比值 \(\frac{\Delta \Phi(x)}{\Delta x}=f(\xi)\text{.}\) 由于 \(f(x)\) 在 \([a, b]\) 上连续, 当 \(\Delta x \rightarrow 0\)时, 有 \(\xi \rightarrow x\text{,}\) 故
\begin{equation*} \Phi^{\prime}(x)=\lim\limits_{\Delta x \rightarrow 0} \frac{\Phi(x+\Delta x)-\Phi(x)}{\Delta x}=\lim\limits_{\xi \rightarrow x} f(\xi)=f(x) . \end{equation*}
即 \(\Phi(x)=\displaystyle \int_{a}^{x} f(t) \mathrm{d} t\) 在 \([a, b]\) 上可导且 \(\Phi^{\prime}(x)=f(x)\text{.}\)
若 \(x=a\text{,}\)取 \(\Delta x>0\text{,}\)则同理可证, \(\Phi_{+}^{\prime}(a)=f(a)\text{;}\) 若 \(x=b\text{,}\) 取 \(\Delta x<0\text{,}\)则同理可证, \(\Phi_{-}^{\prime}(b)=f(b)\text{.}\)
这个定理给出了一个重要结论: 连续函数的可变上限 \(x\) 的定积分, 对上限 \(x\)求导等于变上限代人被积函数. Theorem 6.3.1架起了微分与积分之间的一座桥梁, 并得出了一个重要结论即原函数存在定理。
Theorem 6.3.2 的重要意义是: 一方面, 肯定了连续函数的原函数一定存在, 另一方面, 初步揭示了积分学中定积分与原函数之间的联系. 这就可以通过原函数来计算定积分.

Subsection 6.3.2 牛顿-莱布尼茨公式

Proof.

证 已知函数 \(F(x)\) 是连续函数 \(f(x)\) 的一个原函数, 根据Theorem 6.3.2 知, 变上限的定积分
\begin{equation*} \Phi(x)=\displaystyle \int_{a}^{x} f(t) \mathrm{d} t \end{equation*}
也是 \(f(x)\) 的一个原函数. 则 \(\Phi(x)\) 与 \(F(x)\) 在 \([a, b]\) 上只相差一个常数 \(C\text{,}\) 即
\begin{equation*} \Phi(x)=F(x)+C, \end{equation*}
或
\begin{equation*} \displaystyle \int_{a}^{x} f(t) \mathrm{d} t=F(x)+C \end{equation*}
令 \(x=a\text{,}\) 得
\begin{equation*} 0=\displaystyle \int_{a}^{a} f(x) \mathrm{d} x=F(a)+C \end{equation*}
即 \(C=-F(a)\text{,}\) 于是
\begin{equation*} \displaystyle \int_{a}^{x} f(t) \mathrm{d} t=F(x)-F(a) . \end{equation*}
再令 \(x=b\text{,}\) 得
\begin{equation*} \displaystyle \int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a) . \end{equation*}
为了表示 \(f(x)\) 在 \([a, b]\) 上的定积分和 \(f(x)\) 的原函数 \(F(x)\) 的关系, 把 \(F(b)-\) \(F(a)\) 记成 \([F(x)]_{a}^{b}\text{,}\) 称为函数 \(F(x)\) 在区间 \([a, b]\) 上的增量, 于是有
\begin{equation*} \displaystyle \int_{a}^{b} f(x) \mathrm{d} x=[F(x)]_{a}^{b}=F(b)-F(a) \end{equation*}
这个公式称为牛顿-莱布尼茨公式 (也称为微积分基本公式), 它是计算定积分的基本工具. 按照这个公式,计算定积分只须求出被积函数的任意一个原函数,再求这个原函数 \(F(x)\) 在 \([a, b]\) 上的增量 \([F(x)]_{a}^{b}\) 即可. 这样, 求定积分的问题就归结为求原函数或不定积分的问题.
牛顿-莱布尼茨公式揭示了定积分与不定积分之间的关系: 连续函数 \(f(x)\) 在区间 \([a, b]\) 上的定积分值等于它的一个原函数 \(F(x)\) 在该区间 \([a, b]\) 上的增量. 正因为这种关系,把带有任意常数的原函数的全体称为不定积分, 从而使不定积分的计算方法更具有实际意义.

Example 6.3.4.

例 1 计算 \(\displaystyle \int_{-1}^{1} \frac{\mathrm{d} x}{1+x^{2}}\text{.}\)
Solution.
解 由于 \(\arctan x\) 是 \(\frac{1}{1+x^{2}}\) 的一个原函数, 所以
\begin{equation*} \begin{aligned} \displaystyle \int_{-1}^{1} \frac{\mathrm{d} x}{1+x^{2}} & =[\arctan x]_{-1}^{1}=\arctan 1-\arctan (-1) \\ & =\frac{\pi}{4}-\left(-\frac{\pi}{4}\right)=\frac{\pi}{2} . \end{aligned} \end{equation*}

Example 6.3.5.

例 2 计算 \(\displaystyle \int_{-2}^{-1} \frac{\mathrm{d} x}{x}\text{.}\)
Solution.
解 当 \(x<0\) 时, \(\frac{1}{x}\) 的一个原函数为 \(\ln |x|\text{,}\) 现在积分的区间是 \([-2,-1]\text{,}\) 故
\begin{equation*} \displaystyle \int_{-2}^{-1} \frac{\mathrm{d} x}{x}=[\ln |x|]_{-2}^{-1}=\ln 1-\ln 2=-\ln 2 . \end{equation*}

Example 6.3.6.

例 3 求 \(\displaystyle \int_{0}^{2} f(x) \mathrm{d} x\text{,}\) 其中 \(f(x)=\left\{\begin{array}{ll}x+1, & x \leqslant 1 \\ \frac{1}{2} x^{2}, & x>1\end{array}\right.\text{.}\)
Solution.
解 因为 \(x=1\) 是分段函数 \(f(x)\) 的分段点,所以把区间 \([0,2]\) 分成 \([0,1]\) 和 \([1,2]\) 两个区间, 故有
\begin{equation*} \begin{aligned} \displaystyle \int_{0}^{2} f(x) \mathrm{d} x & =\displaystyle \int_{0}^{1}(x+1) \mathrm{d} x+\displaystyle \int_{1}^{2} \frac{1}{2} x^{2} \mathrm{~d} x \\ & =\left[\frac{1}{2}(x+1)^{2}\right]_{0}^{1}+\left[\frac{1}{6} x^{3}\right]_{1}^{2}=\frac{3}{2}+\frac{7}{6}=\frac{8}{3} . \end{aligned} \end{equation*}
注意 牛顿-莱布尼茨公式中的函数 \(F(x)\) 必须是 \(f(x)\) 在该区间 \([a, b]\) 上的原函数, 如Example 6.3.5 中 \(\frac{1}{x}\) 在 \([-2,-1]\) 上的原函数为 \(\ln |x|\text{,}\) 而Example 6.3.6 中则分别求 \(f(x)\) 在 \([0,1]\) 和 \([1,2]\) 两个区间上的原函数. 由Theorem 6.3.1 已知 \(\frac{\mathrm{d}}{\mathrm{d} x} \displaystyle \int_{a}^{x} f(t) \mathrm{d} t=f(x)\text{.}\) 利用复合函数的求导法则,可进一步得到
\begin{equation*} \frac{\mathrm{d}}{\mathrm{d} x} \displaystyle \int_{a}^{\varphi(x)} f(t) \mathrm{d} t=f[\varphi(x)] \varphi^{\prime}(x) . \end{equation*}
若定积分 \(\displaystyle \int_{a}^{b} f(x) \mathrm{d} x\) 的上、下限分别是函数 \(a(x)\) 和 \(b(x)\text{,}\) 即 \(\displaystyle \int_{a(x)}^{b(x)} f(t) \mathrm{d} t\text{,}\) 因为
\begin{equation*} \displaystyle \int_{a(x)}^{b(x)} f(t) \mathrm{d} t=\displaystyle \int_{c}^{b(x)} f(t) \mathrm{d} t-\displaystyle \int_{c}^{a(x)} f(t) \mathrm{d} t . \end{equation*}
由复合函数求导法则得
\begin{equation*} \frac{\mathrm{d}}{\mathrm{d} x} \displaystyle \int_{a(x)}^{b(x)} f(t) \mathrm{d} t=f[b(x)] b^{\prime}(x)-f[a(x)] a^{\prime}(x) . \end{equation*}

Example 6.3.7.

例 4 已知 \(\Phi(x)=\displaystyle \int_{0}^{x} \frac{\mathrm{d} t}{1+t^{2}}\text{,}\) 求 \(\Phi^{\prime}(2)\text{.}\)
Solution.
解 因为 \(\Phi^{\prime}(x)=\frac{1}{1+x^{2}}\text{,}\) 所以 \(\Phi^{\prime}(2)=\frac{1}{1+2^{2}}=\frac{1}{5}\text{.}\)

Example 6.3.8.

例 5 设 \(\Phi(x)=\displaystyle \int_{0}^{x^{2}} \sqrt{1+t^{3}} \mathrm{~d} t\text{,}\) 求 \(\Phi^{\prime}(x)\text{.}\)
Solution.
解 \(\Phi^{\prime}(x)=\left(\displaystyle \int_{0}^{x^{2}} \sqrt{1+t^{3}} \mathrm{~d} t\right)^{\prime}=\sqrt{1+\left(x^{2}\right)^{3}} \cdot\left(x^{2}\right)^{\prime}=2 x \sqrt{1+x^{6}}\text{.}\)

Example 6.3.9.

例 6 已知 \(\Phi(x)=\displaystyle \int_{x^{2}}^{x^{3}} \sqrt{1+t^{3}} \mathrm{~d} t\text{,}\) 求 \(\Phi^{\prime}(x)\text{.}\)
Solution.
解 \(\Phi^{\prime}(x)=\left(\displaystyle \int_{x^{2}}^{x^{3}} \sqrt{1+t^{3}} \mathrm{~d} t\right)^{\prime}=\sqrt{1+x^{9}} \cdot\left(x^{3}\right)^{\prime}-\sqrt{1+x^{6}} \cdot\left(x^{2}\right)^{\prime}\)
\begin{equation*} =3 x^{2} \sqrt{1+x^{9}}-2 x \sqrt{1+x^{6}} . \end{equation*}

Example 6.3.10.

例 7 求 \(\Phi(x)=\displaystyle \int_{0}^{x} t \mathrm{e}^{-t^{2}} \mathrm{~d} t\) 的极值.
Solution.
解 因为 \(\Phi^{\prime}(x)=\left[\displaystyle \int_{0}^{x} t \mathrm{e}^{-t^{2}} \mathrm{~d} t\right]^{\prime}=x \mathrm{e}^{-x^{2}}\text{,}\) 令 \(\Phi^{\prime}(x)=0\text{,}\) 得驻点 \(x=0\text{,}\)
\begin{equation*} \Phi^{\prime \prime}(x)=\mathrm{e}^{-x^{2}}+x \mathrm{e}^{-x^{2}}(-2 x)=\mathrm{e}^{-x^{2}}\left(1-2 x^{2}\right) . \end{equation*}
而 \(\Phi^{\prime \prime}(0)=1>0\text{,}\) 所以, 当 \(x=0\) 时, \(\Phi(x)\) 有极小值 \(\Phi(0)=0\text{.}\)

Example 6.3.11.

例 8 求 \(\lim\limits_{x \rightarrow 0} \frac{\displaystyle \int_{\cos x}^{1} \mathrm{e}^{-t^{2}} \mathrm{~d} t}{x^{2}}\text{.}\)
Solution.
解 这是 \(\frac{0}{0}\) 型的未定式的极限, 利用洛比达法则计算. 分子可写成 \(-\displaystyle \int_{1}^{\cos x} \mathrm{e}^{-t^{2}} \mathrm{~d} t\text{.}\)
则 \(\frac{\mathrm{d}}{\mathrm{d} x} \displaystyle \int_{\cos x}^{1} \mathrm{e}^{-t^{2}} \mathrm{~d} t=-\frac{\mathrm{d}}{\mathrm{d} x} \displaystyle \int_{1}^{\cos x} \mathrm{e}^{-t^{2}} \mathrm{~d} t=-\mathrm{e}^{-\cos ^{2} x} \cdot(-\sin x)=(\sin x) \mathrm{e}^{-\cos ^{2} x}\text{,}\)
因此
\begin{equation*} \lim\limits_{x \rightarrow 0} \frac{\displaystyle \int_{\cos x}^{1} \mathrm{e}^{-t^{2}} \mathrm{~d} t}{x^{2}}=\lim\limits_{x \rightarrow 0} \frac{\sin x \mathrm{e}^{-\cos ^{2} x}}{2 x}=\frac{1}{2 \mathrm{e}} \end{equation*}

Example 6.3.12.

例 9 讨论函数
\begin{equation*} f(x)= \begin{cases}\frac{\sin 2\left(\mathrm{e}^{x}-1\right)}{\mathrm{e}^{x}-1}, & x>0, \\ 2, & x=0, \\ \frac{1}{x} \displaystyle \int_{0}^{x} \cos ^{2} t \mathrm{~d} t, & x<0\end{cases} \end{equation*}
的连续性.
Solution.
解 显然在 \(x \neq 0\) 时 \(f(x)\) 连续, 只需考虑 \(x=0\) 处 \(f(x)\) 的连续性.
\begin{equation*} \begin{gathered} \lim\limits_{x \rightarrow 0^{+}} f(x)=\lim\limits_{x \rightarrow 0^{+}} \frac{\sin 2\left(\mathrm{e}^{x}-1\right)}{\mathrm{e}^{x}-1}=2=f(0), \\ \lim\limits_{x \rightarrow 0^{-}} f(x)=\lim\limits_{x \rightarrow 0^{-}} \frac{1}{x} \displaystyle \int_{0}^{x} \cos ^{2} t \mathrm{~d} t \stackrel{\text { 洛比达法则 }}{=} \lim\limits_{x \rightarrow 0^{-}} \frac{\cos ^{2} x}{1}=1 \neq f(0), \end{gathered} \end{equation*}
所以 \(f(x)\) 在 \(x=0\) 处间断.

Example 6.3.13.

例 10 设 \(f(x)\) 为连续函数, 证明 \(\displaystyle \int_{0}^{x} f(t)(x-t) \mathrm{d} t=\displaystyle \int_{0}^{x}\left[\displaystyle \int_{0}^{t} f(u) \mathrm{d} u\right] \mathrm{d} t\text{.}\)
Solution.
证 分析 令 \(F(x)=\displaystyle \int_{0}^{x} f(t)(x-t) \mathrm{d} t-\displaystyle \int_{0}^{x}\left[\displaystyle \int_{0}^{t} f(u) \mathrm{d} u\right] \mathrm{d} t\text{,}\) 则需要证明 \(F(x)=0\text{,}\)即要证明 \(F(x)\) 为一个常值函数, 故要证明 \(F^{\prime}(x)=0\text{.}\)
\begin{equation*} \text { 证 令 } \begin{aligned} F(x) & =\displaystyle \int_{0}^{x} f(t)(x-t) \mathrm{d} t-\displaystyle \int_{0}^{x}\left[\displaystyle \int_{0}^{t} f(u) \mathrm{d} u\right] \mathrm{d} t \\ & =x \displaystyle \int_{0}^{x} f(t) \mathrm{d} t-\displaystyle \int_{0}^{x} t f(t) \mathrm{d} t-\displaystyle \int_{0}^{x}\left[\displaystyle \int_{0}^{t} f(u) \mathrm{d} u\right] \mathrm{d} t . \end{aligned} \end{equation*}
对 \(F(x)\) 求导, 有
\begin{equation*} F^{\prime}(x)=\displaystyle \int_{0}^{x} f(t) \mathrm{d} t+x f(x)-x f(x)-\displaystyle \int_{0}^{x} f(u) \mathrm{d} u=0, \end{equation*}
所以 \(F(x)\) 为常数.
又显然有 \(F(0)=0\text{,}\)所以 \(F(x) \equiv 0\text{,}\) 得证.

Subsection 6.3.3 习题 6-3

  1. 解下列各题:
    1. 设 \(\Phi(x)=\displaystyle \int_{0}^{x} \sin t \mathrm{~d} t\text{,}\) 求 \(\Phi^{\prime}\left(\frac{\pi}{4}\right)\text{;}\)
    2. 设 \(\Phi(x)=\displaystyle \int_{0}^{x^{2}} \sqrt{1+t^{2}} \mathrm{~d} t\text{,}\) 求 \(\Phi^{\prime}(x)\text{;}\)
    3. \(\lim\limits_{x \rightarrow 0} \frac{\displaystyle \int_{0}^{x} \sin 2 t \mathrm{~d} t}{x^{2}}\text{;}\)
    4. \(\lim\limits_{x \rightarrow+\infty} \frac{\displaystyle \int_{0}^{x}(\arctan t)^{2} \mathrm{~d} t}{\sqrt{x^{2}+1}}\text{;}\)
    5. \(\lim\limits_{x \rightarrow 0} \frac{\left(\displaystyle \int_{0}^{x} t^{2} \cos t^{2} \mathrm{~d} t\right)^{2}}{\displaystyle \int_{0}^{x^{2}} \sin t^{2} \mathrm{~d} t}\text{.}\)
  2. 计算下列定积分：
    1. \(\displaystyle \int_{1}^{2}(3 x-1) \mathrm{d} x\text{;}\)
    2. \(\displaystyle \int_{4}^{9} \sqrt{x}(1+\sqrt{x}) \mathrm{d} x\text{;}\)
    3. \(\displaystyle \int_{\frac{1}{\sqrt{3}}}^{\sqrt{3}} \frac{\mathrm{d} x}{1+x^{2}}\text{;}\)
    4. \(\displaystyle \int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{\mathrm{d} x}{\sqrt{1-x^{2}}}\text{;}\)
    5. \(\displaystyle \int_{0}^{4}(2-\sqrt{x})^{2} \mathrm{~d} x\text{;}\)
    6. \(\displaystyle \int_{0}^{1} 10^{2 x+1} \mathrm{~d} x\text{;}\)
    7. \(\displaystyle \int_{0}^{\pi}\left(1-\sin ^{3} \theta\right) \mathrm{d} \theta\text{;}\)
    8. \(\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \frac{\ln (\tan x)}{\cos x \sin x} \mathrm{~d} x\text{;}\)
    9. \(\displaystyle \int_{0}^{\frac{1}{2}} \frac{2 x+1}{\sqrt{1-x^{2}}} \mathrm{~d} x\text{;}\)
    10. \(\displaystyle \int_{0}^{\pi} \sqrt{1+\cos 2 x} \mathrm{~d} x\text{.}\)
    1. 设 \(f(x)=\left\{\begin{array}{ll}1+x^{2}, & 0 \leqslant x<1 \\ 2-x, & 1 \leqslant x \leqslant 2,\end{array}\right.\) 求 \(\displaystyle \int_{0}^{2} f(x) \mathrm{d} x\text{;}\)
    2. 求 \(\displaystyle \int_{0}^{2 \pi}|\sin x| \mathrm{d} x\text{.}\)
  4. 设 \(f(x)=\left\{\begin{array}{ll}1+x, & 0 \leqslant x<1, \\ \frac{1}{2} x^{2}, & 1 \leqslant x \leqslant 2,\end{array}\right.\) 求 \(\Phi(x)=\displaystyle \int_{0}^{x} f(t) \mathrm{d} t\) 在 \([0,2]\) 上的表达式, 并讨论 \(\Phi(x)\) 在 \([0,2]\) 上的连续性.
  5. 设 \(f(x)=\left\{\begin{array}{ll}\frac{1}{2} \sin x, & 0 \leqslant x \leqslant \pi, \\ 0, & x<0 \text { 或 } x>\pi,\end{array}\right.\) 求 \(\Phi(x)=\displaystyle \int_{0}^{x} f(t) \mathrm{d} t\) 在 \((-\infty,+\infty)\) 上的表达式.
PrevTopNext