Skip to main content

高等数学: 数字教材

T,谭易兰, C

Section 7.2 定积分在几何方面的应用

Subsection 7.2.1 平面图形的面积

Subsubsection 7.2.1.1 直角坐标系下平面图形的面积

由定积分的几何意义可知, 由曲线 \(y=f(x)(f(x) \geqslant 0)\) 及直线 \(x=a, x=b(a<b)\)与 \(x\) 轴所围成的曲边梯形 (见图 7-1) 的面积
\begin{equation*} A=\displaystyle \int_{a}^{b} f(x) \mathrm{d} x \end{equation*}
其中被积表达式 \(f(x) \mathrm{d} x\) 就是直角坐标系下的面积元素 \(\mathrm{d} A\text{,}\) 即 \(\mathrm{d} A=f(x) \mathrm{d} x\text{.}\)
一般地,由 \(y=f(x), x=a, x=b(a<b)\) 与 \(x\) 轴所围成的曲边梯形面积 (见图 7-2) 为
\begin{equation*} A=\displaystyle \int_{a}^{b}|f(x)| \mathrm{d} x . \end{equation*}
如果平面图形由曲线 \(y=f_{1}(x), y=f_{2}(x)\) \(\left(f_{2}(x)>f_{1}(x)\right), x=a, x=b\) 所围成 (见图 7-3),就用元素法求其面积 \(A\text{.}\)
取 \(x\) 为积分变量, 将 \([a, b]\) 分成 \(n\) 个小区间,任取一小区间 \([x, x+\mathrm{d} x]\text{,}\) 在该区间上的小窄条面积可以用矩形的面积近似代替,矩形的高为 \(f_{2}(x)-\) \(f_{1}(x)\text{,}\)底为 \(\mathrm{d} x\text{,}\) 因此其面积元素
\begin{equation*} \mathrm{d} A=\left[f_{2}(x)-f_{1}(x)\right] \mathrm{d} x, \end{equation*}
从而得
\begin{equation} A=\displaystyle \int_{a}^{b}\left[f_{2}(x)-f_{1}(x)\right] \mathrm{d} x .\tag{7.2.1} \end{equation}
类似地, 由曲线 \(x=\varphi_{1}(y), x=\varphi_{2}(y)\left(\varphi_{2}(y)>\varphi_{1}(y)\right), y=c, y=d(c<d)\) 所 围成的平面图形面积为
\begin{equation} A=\displaystyle \int_{c}^{d}\left[\varphi_{2}(y)-\varphi_{1}(y)\right] \mathrm{d} y,\tag{7.2.2} \end{equation}
其中 \(y\) 为积分变量, \(\mathrm{d} A=\left[\varphi_{2}(y)-\varphi_{1}(y)\right] \mathrm{d} y\) 为面积元素 (见图 7-4).
这样,应用定积分的元素法,不仅可以计算曲边梯形面积,还可以计算一些更为复杂的平面图形的面积.
Example 7.2.1.
例 1 计算由 \(y=x^{2}\) 和 \(y=2 x+3\) 所围的平面图形的面积.
Solution.
解 如图 7-5 所示, 首先要确定平面图形的所在范围, 解方程组
\begin{equation*} \left\{\begin{array}{l} y=x^{2} \\ y=2 x+3 \end{array}\right. \end{equation*}
得两曲线交点 \((-1,1)\) 和 \((3,9)\text{,}\) 从而知图形位于直线 \(x=-1\) 和 \(x=3\) 之间.
取横坐标 \(x\) 为积分变量, 它的变化区间是 \([-1,3]\text{,}\)
任取 \([-1,3]\) 上的小区间 \([x, x+\mathrm{d} x]\text{,}\)则对应的面积元素
\begin{equation*} \mathrm{d} A=\left(2 x+3-x^{2}\right) \mathrm{d} x \end{equation*}
以 \(\mathrm{d} A=\left(2 x+3-x^{2}\right) \mathrm{d} x\) 为被积表达式,在 \([-1,3]\) 上作定积分,便得所求面积为
\begin{equation*} A=\displaystyle \int_{-1}^{3}\left(2 x+3-x^{2}\right) \mathrm{d} x=\left[x^{2}+3 x-\frac{x^{3}}{3}\right]_{-1}^{3}=\frac{32}{3} . \end{equation*}
Example 7.2.2.
例 2 计算由区间 \(\left[\frac{1}{2}, 2\right]\) 上的连续曲线 \(y=\ln x\text{,}\) \(x\) 轴以及直线 \(x=\frac{1}{2}\) 与 \(x=2\) 所围的平面图形面积.
Solution.
解 如图 7-6 所示, 所求图形在 \(x=\frac{1}{2}\) 及 \(x=2\) 之间. 取横坐标 \(x\) 为积分变量, 它的变化区间为 \(\left[\frac{1}{2}, 2\right]\text{,}\)但需要注意的是当 \(x \in\left[\frac{1}{2}, 1\right]\) 时, \(\ln x \leqslant 0\text{,}\) 故在 \(\left[\frac{1}{2}, 1\right]\) 上的任一小区间 \([x, x+\mathrm{d} x]\) 的小曲边梯形的面积元素为 \(\mathrm{d} A=-\ln x \mathrm{~d} x\text{;}\) 当 \(x \in[1,2]\)时, \(\ln x \geqslant 0\text{,}\) 在 \([1,2]\) 上的任一小区间 \([x, x+\mathrm{d} x]\) 的小曲边梯形的面积元素为 \(\mathrm{d} A=\) \(\ln x \mathrm{~d} x\text{.}\) 于是得所求平面图形的面积
\begin{equation*} \begin{aligned} A & =\displaystyle \int_{\frac{1}{2}}^{2}|\ln x| \mathrm{d} x=\displaystyle \int_{\frac{1}{2}}^{1}-\ln x \mathrm{~d} x+\displaystyle \int_{1}^{2} \ln x \mathrm{~d} x \\ & =[x-x \ln x]_{\frac{1}{2}}^{1}+[x \ln x-x]_{1}^{2}=\frac{3}{2} \ln 2-\frac{1}{2} . \end{aligned} \end{equation*}
Example 7.2.3.
例 3 计算抛物线 \(y^{2}=2 x\) 与直线 \(y=x-4\)所围成的图形面积.
Solution.
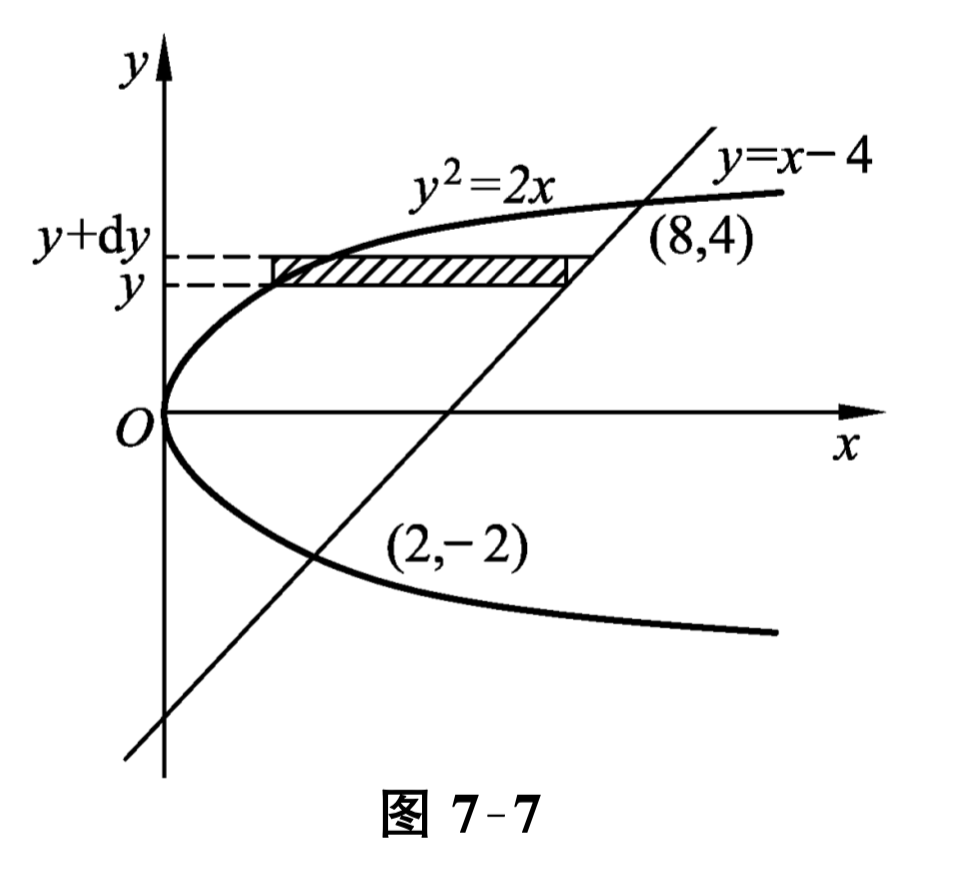
解 如图 7-7 所示, 先求出抛物线与直线的交点, 解方程组
\begin{equation*} \left\{\begin{array}{l} y^{2}=2 x \\ y=x-4 \end{array}\right. \end{equation*}
得交点 \((2,-2)\) 和 \((8,4)\text{.}\)
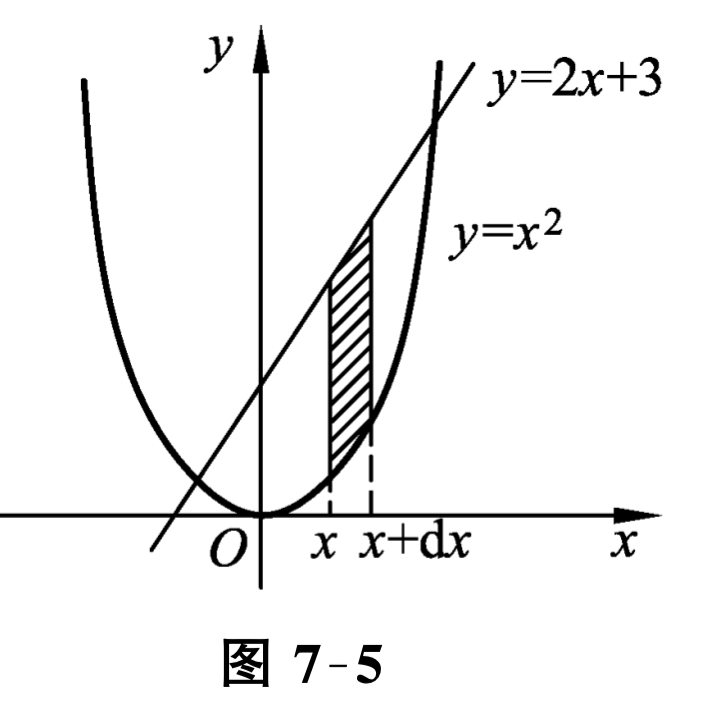
若选取横坐标 \(x\) 为积分变量, 它的变化区间是 \([0,8]\text{.}\) 但在 \([0,2]\) 上的任一小区间 \([x, x+\mathrm{d} x]\text{,}\)
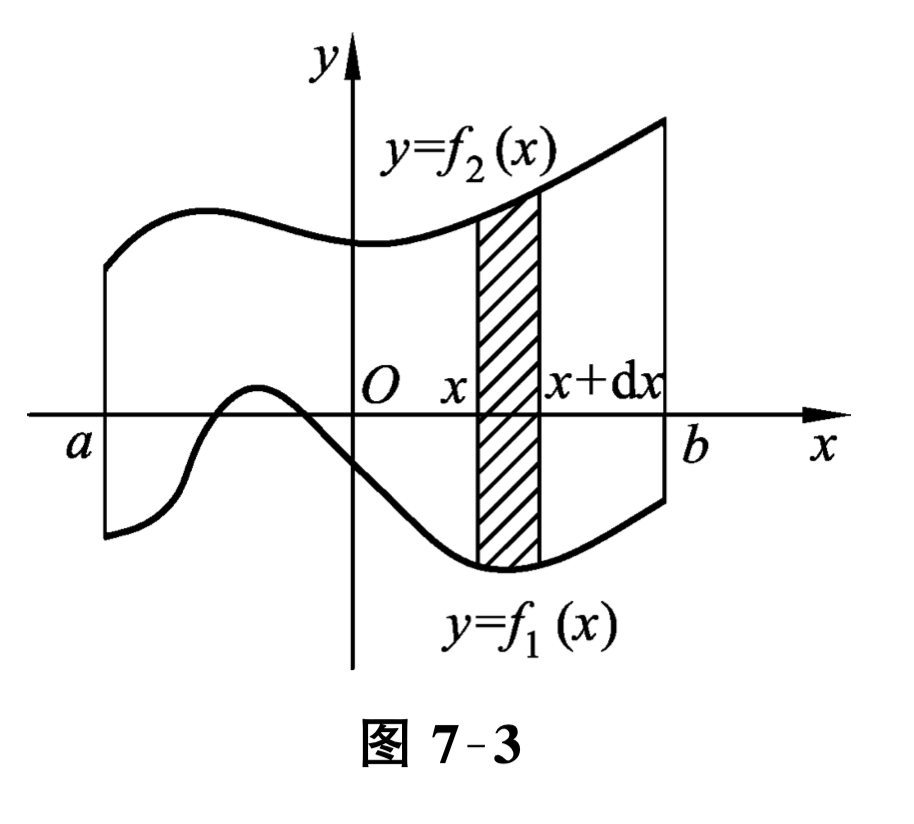
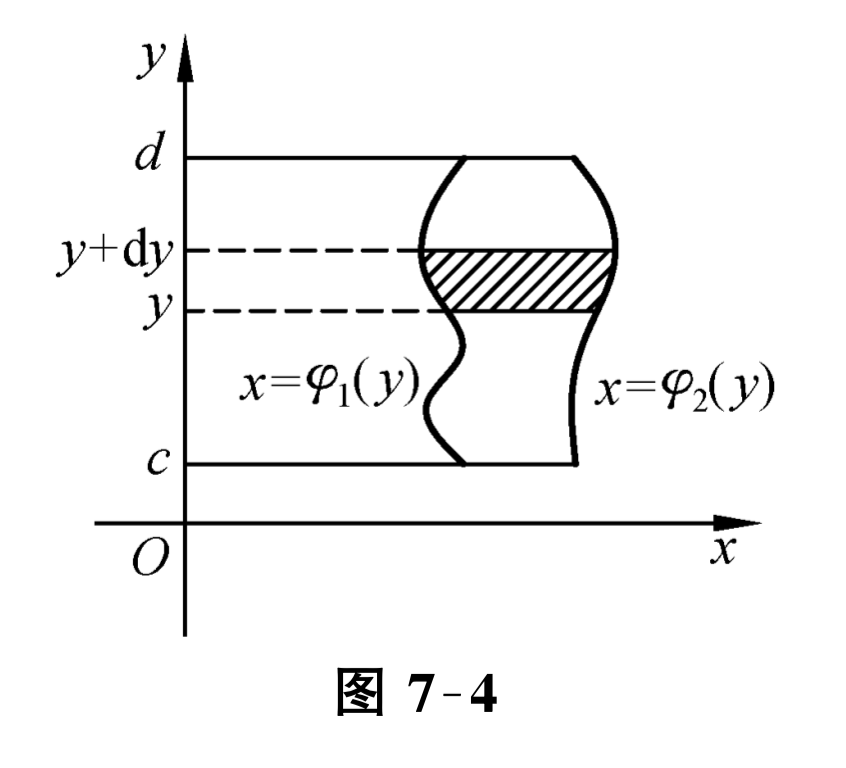
相应的面积元素 \(\mathrm{d} A=2 \sqrt{2 x} \mathrm{~d} x\text{;}\) 而在 \([2,8]\) 上的任一小区间 \([x, x+\mathrm{d} x]\text{,}\)相应的面积元素 \(\mathrm{d} A=(\sqrt{2 x}-x+4) \mathrm{d} x\text{,}\)于是所求图形面积为 \(A=\displaystyle \int_{0}^{2} 2 \sqrt{2 x} \mathrm{~d} x+\displaystyle \int_{2}^{8}(\sqrt{2 x}-x+4) \mathrm{d} x=\left[\frac{4 \sqrt{2}}{3} x^{\frac{3}{2}}\right]_{0}^{2}+\left[\frac{2 \sqrt{2}}{3} x^{\frac{3}{2}}-\frac{x^{2}}{2}+4 x\right]_{2}^{8}=18\text{.}\) 若选取纵坐标 \(y\) 为积分变量, 它的变化区间是 \([-2,4]\text{,}\)相应于 \([-2,4]\) 上任一小区间 \([y, y+\mathrm{d} y]\) 的面积元素
\begin{equation*} \mathrm{d} A=\left(y+4-\frac{1}{2} y^{2}\right) \mathrm{d} y \end{equation*}
从而得
\begin{equation*} A=\displaystyle \int_{-2}^{4}\left(y+4-\frac{1}{2} y^{2}\right) \mathrm{d} y=\left[\frac{y^{2}}{2}+4 y-\frac{1}{6} y^{3}\right]_{-2}^{4}=18 \end{equation*}
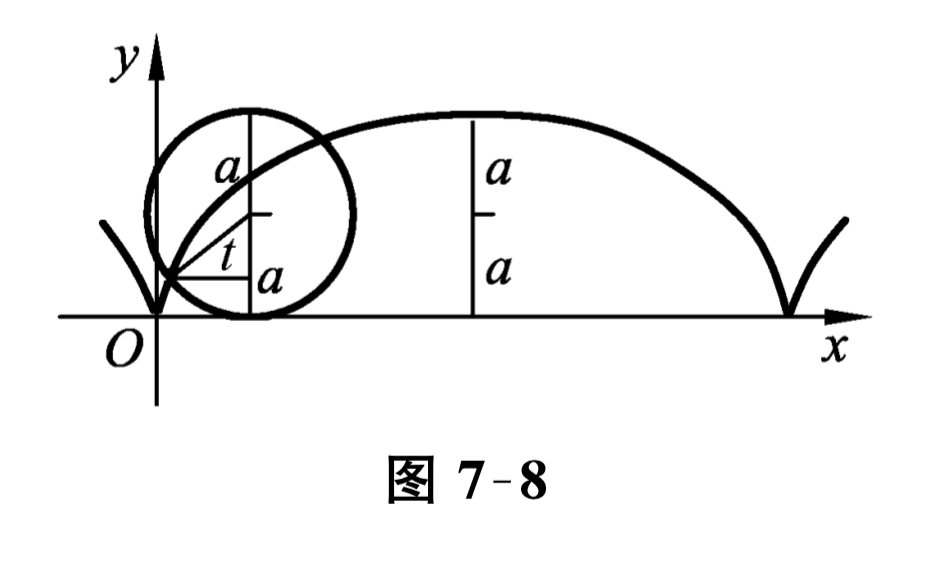
从这个例子可以看出,如果积分变量选择适当,就可以使计算简便. 若曲边梯形的曲边 \(y=f(x)(f(x) \geqslant 0, x \in[a, b])\) 由参数方程
\begin{equation*} \left\{\begin{array}{l} x=\varphi(t), \\ y=\psi(t) \end{array} \quad(\alpha \leqslant t \leqslant \beta)\right. \end{equation*}
给出, 且当变量 \(x\) 从 \(a\) 变到 \(b\) 时,参数 \(t\) 相应地从 \(\alpha\) 变到 \(\beta\text{,}\) 即 \(\varphi(\alpha)=a, \varphi(\beta)=b\text{,}\) 则由曲边梯形的面积公式及定积分的换元公式可得
\begin{equation} A=\displaystyle \int_{a}^{b} y \mathrm{~d} x=\displaystyle \int_{\alpha}^{\beta} \psi(t) \varphi^{\prime}(t) \mathrm{d} t .\tag{7.2.3} \end{equation}
Example 7.2.4.
例 4 计算旋轮线 (摆线) \(x=a(t-\sin t), y=a(1-\cos t)\) 的一拱 \((0 \leqslant t \leqslant 2 \pi)\) 与 \(x\) 轴所围图形 (见图 7-8) 的面积.
Solution.
解 \(x=a(t-\sin t), y=a(1-\cos t)\text{,}\) \(\mathrm{d} x=a(1-\cos t) \mathrm{d} t\text{,}\)
\begin{equation*} \begin{aligned} A & =\displaystyle \int_{0}^{2 \pi} a(1-\cos t) \cdot a(1-\cos t) \mathrm{d} t \\ & =a^{2} \displaystyle \int_{0}^{2 \pi}\left(1-2 \cos t+\cos ^{2} t\right) \mathrm{d} t=3 \pi a^{2} . \end{aligned} \end{equation*}

Subsubsection 7.2.1.2 极坐标系下平面图形的面积

对于某些平面图形,利用极坐标计算它们的面积较为简便.
在极坐标系下, 由连续曲线 \(r=r(\theta)(\alpha \leqslant \theta \leqslant \beta)\)及射线 \(\theta=\alpha, \theta=\beta\) 所围成的平面图形称为曲边扇形 (见图 7-9),下面计算它的面积 \(A\text{.}\)
取极角 \(\theta\) 为积分变量, 它的变化区间为 \([\alpha, \beta]\text{,}\)在 \([\alpha, \beta]\) 上任取一小区间 \([\theta, \theta+\mathrm{d} \theta]\text{,}\) 该区间上的小
曲边扇形的面积可以用半径 \(r=r(\theta)\text{,}\) 中心角为 \(\mathrm{d} \theta\) 的小扇形的面积来近似代替,因此得到曲边扇形的面积元素为
\begin{equation*} \mathrm{d} A=\frac{1}{2}[r(\theta)]^{2} \mathrm{~d} \theta \end{equation*}
从而得曲边扇形的面积
\begin{equation} A=\frac{1}{2} \displaystyle \int_{\alpha}^{\beta} r^{2}(\theta) \mathrm{d} \theta .\tag{7.2.4} \end{equation}
Example 7.2.5.
例 5 计算心形线 \(r=a(1+\cos \theta)(a>0)\) 所围成的图形的面积.
Solution.
解 如图 7-10 所示, 心形线所围图形对称于极轴, 因此所求图形的面积 \(A\) 是极轴上方图形面积 \(A_{1}\)的两倍.
对于极轴上方部分图形, 取 \(\theta\) 为积分变量, \(\theta\) 的变化区间为 \([0, \pi]\text{,}\)于是得
\begin{equation*} \begin{aligned} A & =2 A_{1}=2 \times \frac{1}{2} \displaystyle \int_{0}^{\pi} a^{2}(1+\cos \theta)^{2} \mathrm{~d} \theta \\ & =a^{2} \displaystyle \int_{0}^{\pi}\left(1+2 \cos \theta+\cos ^{2} \theta\right) \mathrm{d} \theta \\ & =a^{2}\left[\frac{3}{2} \theta+2 \sin \theta+\frac{1}{4} \sin 2 \theta\right]_{0}^{\pi}=\frac{3}{2} \pi a^{2} . \end{aligned} \end{equation*}
Example 7.2.6.
例 6 计算双纽线 \(r^{2}=a^{2} \cos 2 \theta(a>0)\) 所围图形的面积.
Solution.
解 如图 7-11 所示, 根据双纽线的对称性, 所求图形的面积 \(A\) 是图中阴影部分面积 \(A_{1}\) 的 4 倍.
\begin{equation*} \begin{aligned} A & =4 A_{1}=4 \displaystyle \int_{0}^{\frac{\pi}{4}} \frac{1}{2} a^{2} \cos 2 \theta \mathrm{d} \theta \\ & =\left[a^{2} \cdot \sin 2 \theta\right]_{0}^{\frac{\pi}{4}}=a^{2} . \end{aligned} \end{equation*}

Subsection 7.2.2 体积

Subsubsection 7.2.2.1 平行截面面积为已知的立体体积

设有一立体如图 7-12 所示, 其垂直于 \(x\) 轴的截面面积是 \(x\) 的连续函数 \(A(x)(a \leqslant x \leqslant b)\text{,}\) 横坐标 \(x=a\) 与 \(x=b\) 分别对应于立体两端的截面 (截面可以缩成一点), 也可以用定积分来计算立体体积.
取横坐标 \(x\) 为积分变量, 它的变化区间为
\([a, b]\text{,}\) 相应于 \([a, b]\) 上任一小区间 \([x, x+\mathrm{d} x]\) 的小立体, 可以近似看成底面积为 \(A(x)\text{,}\) 高为 \(\mathrm{d} x\) 的扁柱体, 则体积元素
\begin{equation*} \mathrm{d} V=A(x) \mathrm{d} x \end{equation*}
以 \(\mathrm{d} V=A(x) \mathrm{d} x\) 为被积表达式,在 \([a, b]\) 上作定积分,便得立体体积
\begin{equation} V=\displaystyle \int_{a}^{b} A(x) \mathrm{d} x\tag{7.2.5} \end{equation}
Example 7.2.7.
例 7 计算以半径 \(R\) 的圆为底, 且垂直于底面上一条固定直径的所有截面都是等边三角形的立体体积.
Solution.
解 如图 7-13 所示, 以固定直径为 \(x\) 轴, 圆心为原点建立坐标系. 过 \(x\) 轴上点 \(x\) 作截面, 得等边三角形,则其边长为 \(a=2 \sqrt{R^{2}-x^{2}}\text{,}\) 从而得截面面积
\begin{equation*} A(x)=\frac{1}{2} a \cdot \frac{\sqrt{3}}{2} a=\sqrt{3}\left(R^{2}-x^{2}\right) . \end{equation*}
取 \(x\) 为积分变量, 它的变化区间为 \([-R, R]\text{,}\)再根据图形的对称性,得
\begin{equation*} V=2 \displaystyle \int_{0}^{R} A(x) \mathrm{d} x=2 \sqrt{3} \displaystyle \int_{0}^{R}\left(R^{2}-x^{2}\right) \mathrm{d} x=\frac{4 \sqrt{3}}{3} R^{3} . \end{equation*}
(7.2.5) 非常重要, 它不但给出已知截面面积 \(A(x)\) 的物体体积的计算公式,而且是重积分计算中将二重积分转换为二次积分的关键公式.

Subsubsection 7.2.2.2 旋转体的体积

旋转体是由一个平面图形绕该平面内一条直线旋转一周而成的立体, 该直线叫做旋转轴. 设在 \(x O y\) 平面内由曲线 \(y=f(x)\) 与直线 \(x=a\text{,}\) \(x=b, y=0\) 所围成的平面图形绕 \(x\) 轴旋转一周而成的旋转体. 现在计算该旋转体的体积.
过区间 \([a, b]\) 上任一点 \(x\text{,}\) 作垂直于 \(x\) 轴的截面,它是一个半径为 \(y=f(x)\) 的圆 (见图 7-14), 因此横截面的面积是
\begin{equation*} A(x)=\pi y^{2}=\pi[f(x)]^{2} . \end{equation*}
取横坐标为积分变量, 它的变化区间是 \([a, b]\text{,}\)于是由(7.2.5)得旋转体的体积
\begin{equation} V=\displaystyle \int_{a}^{b} \pi[f(x)]^{2} \mathrm{~d} x .\tag{7.2.6} \end{equation}
Example 7.2.8.
例 8 计算由 \(x y=2, x=2, x=4\) 与 \(x\) 轴所围成的图形绕 \(x\) 轴旋转所成旋转体的体积。
Solution.
解 由 \(x y=2\text{,}\) 得 \(y=\frac{2}{x}\text{,}\) 则
\begin{equation*} \begin{gathered} \mathrm{d} V=\pi y^{2} \mathrm{~d} x=\pi\left(\frac{2}{x}\right)^{2} \mathrm{~d} x \\ V=\displaystyle \int_{2}^{4} \pi\left(\frac{2}{x}\right)^{2} \mathrm{~d} x=4 \pi\left[-\frac{1}{x}\right]_{2}^{4}=\pi . \end{gathered} \end{equation*}
类似可得: 由曲线 \(x=\varphi(y)\text{,}\) 直线 \(y=c, y=d\) \((c<d)\) 与 \(y\) 轴所围成的曲边梯形,绕 \(y\) 轴旋转一周而成的旋转体 (见图 7-15) 的体积为
\begin{equation} V=\pi \displaystyle \int_{c}^{d}[\varphi(y)]^{2} \mathrm{~d} y\tag{7.2.7} \end{equation}
Example 7.2.9.
例 9 计算由 \(y=\sqrt{2 x-4}, x=2, x=4\) 与 \(x\) 轴所围图形分别绕 \(x\) 轴、 \(y\) 轴旋转所成旋转体的体积.
Solution.
解 (1) 绕 \(x\) 轴旋转时, 取 \(x\) 为积分变量, 它的变化区间是 \([2,4]\text{,}\) 见图 7-16.
\begin{equation*} \begin{gathered} \mathrm{d} V=\pi y^{2} \mathrm{~d} x=\pi(2 x-4) \mathrm{d} x \\ V=\displaystyle \int_{2}^{4} \pi(2 x-4) \mathrm{d} x=\pi\left[x^{2}-4 x\right]_{2}^{4}=4 \pi . \end{gathered} \end{equation*}
(2)绕 \(y\) 轴旋转时,取 \(y\) 为积分变量,它的变化区间是 \([0,2]\text{,}\)如图 7-17 阴影所示.
\begin{equation*} \begin{gathered} x_{1}=\frac{y^{2}+4}{2}, x_{2}=4, \\ V=\pi \displaystyle \int_{0}^{2} x_{2}^{2} \mathrm{~d} y-\pi \displaystyle \int_{0}^{2} x_{1}^{2} \mathrm{~d} y=\pi \displaystyle \int_{0}^{2} 4^{2} \mathrm{~d} y-\pi \displaystyle \int_{0}^{2}\left(\frac{y^{2}+4}{2}\right)^{2} \mathrm{~d} y \\ =32 \pi-\frac{224}{15} \pi=\frac{256}{15} \pi . \end{gathered} \end{equation*}

Subsection 7.2.3 平面曲线的弧长

设有一段平面曲线弧 \(\overparen{A B}\) (见图 7-18),在弧 \(\overparen{A B}\) 上任取分点 \(A=M_{0}, M_{1}, \cdots, M_{n}=\) \(B\text{,}\) 依次连接相邻分点得一内接折线.
这条折线的长度是 \(L=\sum\limits_{k=1}^{n}\left|M_{k-1} M_{k}\right|\text{,}\)当分点的数目无限增加且每个小段 \(\overline{M_{k-1} M_{k}}\)都缩向一点时, 若折线长 \(L\) 的极限存在, 则称此极限为曲线弧 \(\overparen{A B}\) 的弧长, 并称此曲线弧是可求长的. 对于光滑曲线弧, 有如下结论:
这个定理不加证明. 由于光滑曲线弧是可求长的,故可应用定积分来计算弧长.下面用定积分的元素法来讨论平面曲线弧长的计算.
  1. 设曲线弧 \(\overparen{A B}\) 的方程为 \(y=f(x), x \in[a, b]\text{,}\) 其中 \(f(x)\) 在 \([a, b]\) 上具有一阶连续导数.
取横坐标 \(x\) 为积分变量, 它的变化区间为 \([a, b]\text{.}\) 曲线 \(y=f(x)\) 上相应于 \([a, b]\) 的任一小区间 \([x, x+\mathrm{d} x]\) 的一段弧的长度可用该曲线在点 \((x, f(x))\) 处的切线上相应的直线段长度近似代替 (见图 7-19), 从而得弧长微分 (参见 4.5.1 弧微分公式(4.5.1))
\begin{equation*} \mathrm{d} s=\sqrt{(\mathrm{d} x)^{2}+(\mathrm{d} y)^{2}}=\sqrt{1+y^{\prime 2}} \mathrm{~d} x, \end{equation*}
于是得所求弧长为
\begin{equation} s=\displaystyle \int_{a}^{b} \sqrt{1+y^{\prime 2}} \mathrm{~d} x\tag{7.2.8} \end{equation}
(2)如果曲线弧 \(\overparen{A B}\) 的方程由参数方程 \(\left\{\begin{array}{l}x=\varphi(t), \\ y=\psi(t)\end{array}(t \in[\alpha, \beta])\right.\) 给出, 其中 \(\varphi(t)\text{,}\) \(\psi(t)\) 在 \([\alpha, \beta]\) 上具有连续导数. 取参数 \(t\) 为积分变量, 它的变化区间为 \([\alpha, \beta]\text{,}\) 相应于 \([\alpha, \beta]\) 上的任一小区间 \([t, t+\mathrm{d} t]\) 的弧长微分为
\begin{equation*} \mathrm{d} s=\sqrt{(\mathrm{d} x)^{2}+(\mathrm{d} y)^{2}}=\sqrt{\varphi^{\prime 2}(t)+\psi^{\prime 2}(t)} \mathrm{d} t, \end{equation*}
于是所求弧长为
\begin{equation} s=\displaystyle \int_{\alpha}^{\beta} \sqrt{\varphi^{\prime 2}(t)+\psi^{\prime 2}(t)} \mathrm{d} t\tag{7.2.9} \end{equation}
(3)曲线弧 \(\overparen{A B}\) 的方程由极坐标方程 \(r=r(\theta), \theta \in\left[\theta_{1}, \theta_{2}\right]\) 给出, 其中 \(r(\theta)\) 在 \(\left[\theta_{1}, \theta_{2}\right]\) 上具有连续导数. 由直角坐标与极坐标的关系可得
\begin{equation*} \left\{\begin{array}{l} x=r(\theta) \cos \theta, \\ y=r(\theta) \sin \theta, \end{array} \quad \theta \in\left(\theta_{1}, \theta_{2}\right)\right. \end{equation*}
于是
\begin{equation*} \mathrm{d} s=\sqrt{x^{\prime 2}(\theta)+y^{\prime 2}(\theta)} \mathrm{d} \theta=\sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} \mathrm{d} \theta, \end{equation*}
从而得所求弧长
\begin{equation} s=\displaystyle \int_{\theta_{1}}^{\theta_{2}} \sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} \mathrm{d} \theta\tag{7.2.10} \end{equation}

Example 7.2.11.

例 10 计算 \(y=\ln \left(1-x^{2}\right)\) 上从 \(x=0\) 到 \(x=\frac{1}{2}\) 的一段弧长.
Solution.
解 \(y^{\prime}=\frac{-2 x}{1-x^{2}}, 1+y^{\prime 2}=\left(\frac{1+x^{2}}{1-x^{2}}\right)^{2}\text{.}\) 从而得弧长微分
\begin{equation*} \mathrm{d} s=\sqrt{1+y^{\prime 2}} \mathrm{~d} x=\frac{1+x^{2}}{1-x^{2}} \mathrm{~d} x \end{equation*}
于是所求弧长
\begin{equation*} \begin{aligned} s & =\displaystyle \int_{0}^{\frac{1}{2}} \frac{1+x^{2}}{1-x^{2}} \mathrm{~d} x=\displaystyle \int_{0}^{\frac{1}{2}}\left(-1+\frac{2}{1-x^{2}}\right) \mathrm{d} x \\ & =\left[-x+\ln \left|\frac{1+x}{1-x}\right|\right]_{0}^{\frac{1}{2}}=-\frac{1}{2}+\ln 3 . \end{aligned} \end{equation*}

Example 7.2.12.

例 11 一物体的运动规律为 \(x=3 \cos 2 t, y=3 \sin 2 t\text{,}\) 计算物体从 \(t=0\) 到 \(t=\pi\)所移动的距离.
Solution.
解
\begin{equation*} x^{\prime}(t)=-6 \sin 2 t, y^{\prime}(t)=6 \cos 2 t \end{equation*}
于是得
\begin{equation*} s=\displaystyle \int_{0}^{\pi} \sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} \mathrm{d} t=\displaystyle \int_{0}^{\pi} \sqrt{(-6 \sin 2 t)^{2}+(6 \cos 2 t)^{2}} \mathrm{~d} t=\displaystyle \int_{0}^{\pi} 6 \mathrm{~d} t=6 \pi . \end{equation*}

Example 7.2.13.

例 12 计算心形线 \(r=a(1+\cos \theta)(a>0)\) 的全长.
Solution.
解 心形线如图 7-10 所示, 由于心形线在 \([0, \pi]\) 与 \([\pi, 2 \pi]\) 上的弧长相等, 故只需计算 \([0, \pi]\) 上的弧长,再乘以 2 即可.
\begin{equation*} \begin{gathered} r=a(1+\cos \theta), \quad r^{\prime}=-a \sin \theta, \\ r^{2}=a^{2}(1+\cos \theta)^{2}, \quad r^{\prime 2}=a^{2} \sin ^{2} \theta, \end{gathered} \end{equation*}
于是由(7.2.10)得心形线的全长为
\begin{equation*} s=2 \displaystyle \int_{0}^{\pi} \sqrt{a^{2}(1+\cos \theta)^{2}+a^{2} \sin ^{2} \theta} \mathrm{d} \theta=2 a \displaystyle \int_{0}^{\pi} \sqrt{2(1+\cos \theta)} \mathrm{d} \theta \end{equation*}
\begin{equation*} =4 a \displaystyle \int_{0}^{\pi} \cos \frac{\theta}{2} \mathrm{~d} \theta=8 a \end{equation*}

Subsection 7.2.4 习题 7-2

  1. 求由下列平面曲线所围图形的面积:
    1. \(y=x^{3}, y=1, x=0\text{;}\)
    2. \(y=x^{2}, y^{2}=x\text{;}\)
    3. \(y=\frac{1}{x}, y=x, x=2\text{;}\)
    4. \(y=\mathrm{e}^{x}, y=\mathrm{e}, x=0\text{;}\)
    5. \(y=\sqrt{x}, y=x\text{;}\)
    6. \(y=2 x, y=3-x^{2}\text{;}\)
    7. \(y=x^{2}, y=x, y=2 x\text{;}\)
    8. \(y=\sin x, y=\cos x, x=0, x=\frac{\pi}{2}\text{.}\)
  2. 抛物线 \(y^{2}=2 x\) 将圆 \(x^{2}+y^{2}=8\) 的面积分为两部分, 这两部分的面积之比如何?
  3. 求抛物线 \(y=-x^{2}+4 x-3\) 及其在点 \((0,-3)\) 和 \((3,0)\) 处的切线所围成的图形面积.
  4. 求两抛物线 \(y^{2}=1+x, y^{2}=1-x\) 所围成的图形面积.
  5. 求由下列曲线所围成的平面图形的面积:
    1. \(x=a \cos ^{3} t, y=a \sin ^{3} t\text{;}\)
    2. \(r=2 a \cos \theta\text{;}\)
    3. \(r=a \sin 3 \theta\text{.}\)
  6. 求下列旋转体的体积:
    1. 由曲线 \(y=x^{2}, x=y^{2}\) 所围平面图形,绕 \(x\) 轴旋转;
    2. 曲线 \(y=\sin x, y=0(0 \leqslant x \leqslant \pi)\) 所围图形, 分别绕 \(x\) 轴和 \(y\) 轴旋转;
    3. 曲线 \(y=x^{3}, x=2, y=0\) 所围成的图形,分别绕 \(x\) 轴和 \(y\) 轴旋转.
  7. 平面图形是由曲线 \(y=\mathrm{e}^{x}, y=\mathrm{e}^{-x}\) 及 \(x=1\) 所围成, 求
    1. 该平面图形的面积;
    2. 该平面图形绕 \(x\) 轴旋转而成的旋转体体积.
  8. 求以半径为 \(R\) 的圆为底, 平行且等于底圆直径的线段为顶,高为 \(h\) 的正䢃锥体体积 (见图 7-20).
  9. 计算下列曲线的弧长:
    1. \(y=\ln x, \sqrt{3} \leqslant x \leqslant \sqrt{8}\text{;}\)
    2. \(y=x^{\frac{3}{2}}, 0 \leqslant x \leqslant 4\text{;}\)
    3. \(x=t^{2}, y=t^{3}, 1 \leqslant t \leqslant 2\text{;}\)
    4. \(x=a(t-\sin t), y=a(1-\cos t), 0 \leqslant t \leqslant 2 \pi\text{;}\)
    5. \(r=\mathrm{e}^{a \theta}, 0 \leqslant \theta \leqslant \varphi_{0}\text{.}\)
  10. 计算星形线 \(x=a \cos ^{3} t, y=a \sin ^{3} t\) 的全长.
PrevTopNext